Последние комментарии
Лаборатория космических исследований
Ульяновская секция Поволжского отделения Российской Академии Космонавтики им. К. Э. Циолковского
Ульяновский Государственный Университет
Академия космонавтики
Геопортал
Проекты
- Космическая Эра
- RMR_astra
- Беседы о Космосе
- Другие миры
- Космическое сознание
- Неочевидное вероятное
- Наблюдение МКС
- Великая Победа
- Жизнь Солнца
- Практикум Космофизика
- Спутник - на урок!
- Гранты РФФИ
- Статьи
- Авиация
- Астрономия
- Обсерватории России
- Загадочные небеса
- Астрофизика
- Космонавтика
- Физика газового разряда
- Роботы
- CanSat в России
Кафедра Теор. Физики
Знание-Сила
Конференции
Сотрудники
Вход для пользователей
Наши партнеры
Солнце в реальном времени
Последние обновления
-
1 неделя 5 дней
-
1 неделя 5 дней
-
2 недели 1 день
-
2 недели 1 день
-
2 недели 1 день
Последние комментарии
- Что внутри частиц?
1 неделя 5 дней назад - А что там внутри?
1 неделя 5 дней назад - Вспышки мощные
2 недели 2 дня назад - Николаю Стрижакову лично
2 недели 3 дня назад - Серия солнечных вспышек
2 недели 3 дня назад - Спасибо большое!
3 недели 3 часа назад - Аврора
3 недели 3 часа назад - Большая точность не обязательна
3 недели 8 часов назад - Николай, благодарим
3 недели 9 часов назад - Уважаемая Полина!
3 недели 11 часов назад
ЛКИ, Ульяновск, Российская Федерация © 2006 - 2026



Валерия, спасибо за интересную информацию.
Без подготовки увидеть такую картину в небе - точно поверишь, что это НЛО!
Остается только сожалеть, что не смогли стать "первооткрывателями". Будем наблюдать ещё с большим интересом загадочные небеса.
Уважаемые читатели интернета, не успел поделиться своей приметой о влиянии Луны (точнее её фазы полнолуния)) на воздушные течения в средних широтах Земли, как Луна «обиделась» на мою малозаметную фразу («и менее выраженное влияние в новолуние») и устроила настоящий погром в своё новолуние (7-8(полнолуние в апреле) +15= 22-23(новолуние) Москве (см. ссылку
https://aif.ru/society/nature/shtormovoy_veter_v_moskve_za_sutki_povalil_bolee_130_derevev ):
« Более 130 деревьев было повалено штормовым ветром в Москве за прошедшие сутки, передаёт Москва 24. … Сообщается, что порывы ветра временами достигали 23 м/с. Из-за стихии оказались повреждены несколько десятков автомобилей ( *)точнее 64 авто). Среди людей пострадавших нет… Москвичи снимали из окон своих домов снегопад, ливень и гнущиеся от ветра деревья…»
Так что, придётся давать более уточнённый вариант этой проверенной десятилетиями погодной приметы:
« Наступление полнолуния и новолуния сопровождается интенсивным вторжением северо-западных ветров (с вероятностью до 85-90%) из приполярной области Земли и по прошествии от 3-6 дней после наступления этих фаз Луны для средних широт Земли на один-два дня происходит резкое похолодание из-за принесенного арктического холодного воздуха». Аналогичное явление должно наблюдаться и в средних широтах Южного полушария Земли.
Сегодня, рано утром, 26 апреля у нас, в Дубне на Волге, на севере Московской области (130 км севернее Москвы) мороз под утро в 5 час составил минус 4 градуса, но уже через пару часов после восхода Солнца воздух прогрелся почти до нуля градусов. А вот ветер, разгулявшийся 22 апреля, был довольно сильным и штормовым, что бывает весьма редко.
Подводя итог, можно сказать, что Луна является одним из главных факторов перемешивания слоёв атмосферы в средних северных (и южных) широтах Земли с периодом равным половине синодического периода Луны (~29,5 дней), т.е. ~ 15 дней. Иначе говоря, Луна выполняет роль своеобразного генератора роторного водушного насоса, перемешивающего воздух от приполюсных областей Земли с воздухом приэкваторного пояса, закручивая воздушный поток при движении из северной области в средние широты против часовой стрелки за счёт Кориолисова ускорения, (ну куда же без него: и на Земле, в атмосфере, и в либрационных точках Лагранжа L4 (L5)). Кстати, привет, тов. А.А.Астахову с его «полу-фиктимым и полу-реальным» Кориолисовым ускорением: не надо путать фиктивное и реальное. Молодые, не повторяйте таких ошибок, лучше учитесь на чужих ошибках. (Это в порядке рекламы, типа подписывайтесь на наш телеграмм-канал. Шутка.).
Георгий 26.04.2020г. 7 час 48мин. Время Моск.
Как отличается реальный репортаж от официальной версии. Можно только поразиться самообладанию всех причастных к первым полетам в Космос.
Запомнились слова Б. Е. Чертока на конференции в Калуге в 2011 году. Ему было тогда 99 лет:
Впервые узнаю, что полет Юрия Гагарина длился 106 минут. Значит, из-за недолета 180 км не был совершен полный оборот вокруг Земли? Это не очень существенное отклонение для такого события. Но американцы что-то писали по этому поводу. Особенно после того, как были опубликованы доказательства, что американцев на Луне не было.
Также неожиданно было узнать, что по радио передали о полете до того, как нашли Юрия Гагарина после приземления. Разумнее было сообщить только после успешного завершения полета. Это всегда подчеркивали очевидцы тех событий.
Для полнолуния 7-8 апреля 2020 года взаимосвязь подтвердилась на 100 %. Вечером 12 апреля в Ульяновской области неожиданно выпал снег, и температура понизилась до отрицательных температур.
Конечно, необходимо проанализировать за все время наблюдения метеорологов. Но это явление действительно содержит не только научный интерес, но и практический.
Лично у меня своеобразное отношение к любым праздникам и датам.
Когда в определенный день отмечают День космонавтики, День защитников Отечества, Женский день... у меня, к сожалению, не возникает праздничного настроения. Есть ценности, которые присутствуют в памяти и сознании человека всегда. Мне не совсем понятно, почему о каких-то событиях надо вспоминать в определенные даты.
С моей (возможно, больше никто не разделяет) точки зрения Космос значим для нас всегда, как и честность, доброта, чувства к близким по духу людям в душе.
Но отдавая дань общепринятым традициям, выставляю статью о Юрии Гагарине первым на главной странице сайта в День космонавтики. 2020 года.
Уважаемый ВИ0540!
К сожалению, все это осреднённые данные и даже отдельные экстремумы температур неизвестно в какому месяцу и году привязаны и,следовательно, неизвестно какой фазе Луны они соответствуют. Это как "средняя температура по больнице", не привязанная к конкретному человеку (фазе Луны). Нужна привязка всех 13 полнолуний ( и, в меньшей степени влияния новолуний) на графики ежедневных температур,например, в течение одного года для в данной области, вот тогда это эффект и будет явно заметен.
По моим наблюдениям (картофелевода уже с 35-летним стажем с наблюдениями по весне за возможными заморозками), метод даёт "осечки" с среднем ~2 раза в год, что вполне неплохо для такого "ветреного" явления как погода.
С уважением. Георгий. 10.02.2020г. 17час05мин. Время.моск.
Спасибо, Георгий за познавательную информацию.
Действительно, не обращали на это внимание. У нас в Ульяновске после полнолуния 7 апреля 2020 г. тоже наступило заметное похолодание 10 апреля. Исследование связи фаз Луны и погоды достойно внимания.
У нас за погодой уже много лет внимательно следит ВИ0540. На сайте публиковались графики и таблицы температуры, правда, без указания лунных фаз. Но даты полнолуний можно найти за все годы в интернете.
Вот интересная статья уважаемого ВИ0540 о многолетних наблюдениях за погодой.
К вопросу о похолоданиях в средних широтах Земли после полнолуния
Уважаемая Полина, на сайте часто отмечают такие красочные явления как полнолуние (суперлуние). И мне хочется «внести свои пять копеек» в это явление.
Уже более двадцати лет нахожу подтверждение свое теории кратковременных похолоданий в средней полосе широт (Московская область) Земли после каждого из полнолуний:
« После наступления полнолуния течение недели (ближе к 3-6 дню после полнолуния для широты Московской области) почти всегда (с вероятностью 85-90%) начинается интенсивное вторжение северо-западного ветра и на один-два дня происходит резкое похолодание из-за принесенного арктического холодного воздуха».
У синоптиков на любое похолодание всегда один ответ «циклоны» да «антициклоны», а что реальных причин этих явлений перемещений этих циклонов они упорно не хотят замечать, видимо, плохо учились в школе в своё время. Решил поискать в интернете что-либо про влияние притяжения Луны на атмосферу Земли. И что же нашёл, только не падайте со стула, ссылку на автора чуть ли не 250-летней давности о том, что !по его мнению! фазы Луны не влияют на погоду. «Обалдеть»! А что за последние сто лет сплошных метеонаблюдений ничего так и не удалось выяснить ничего более полезного, например, для сельского хозяйства? То, что притяжение Луны влияет на приливы в морях наука признаёт, а вот синоптики влияния притяжения Луны на изменение «розы ветров» в атмосфере Земли и видеть не хотят, или им не до этого! А ведь достаточно было бы нарисовать графики изменения ежедневной температуры, отметив на них фазы Луны, и путём математической обработки установить корреляцию между фазами полнолуния (и менее выраженное влияние новолуния).
Конечно, примета, не ахти какая. Но для тех, кто трудится на Земле имеет большое значение для того, чтобы знать когда ожидать появление кратковременных заморозков, особенно в начале очередного сезона (апрель-июнь) для защиты, например, появившихся ростков картофеля от заморозков. А ведь эта примета буквально вертится перед носом у всех в средней полосе! Но что-то ничего нет по этому поводу в интернете.
Расписывать механику влияния нарочно не буду, попробуйте её сами обосновать, а также и время появления похолодания в средней широте на 3-6 день!
Кстати, можете проверить этоту примету, полнолуние произошло 7-8 апреля. Похоладание в средних широтах ждём 7-8 + (3-6) апреля. В Мурманске снег уже всё засыпал, там севернее. А как там, в Сибири?
Всего самого наилучшего и не болейте!
Георгий. 10.04.2020г 9час.55мин. Время Моск.
Георгий, спасибо за оперативный ответ. Ваш комментарий немного подкорректировала (надеюсь, Вы не будете против) в соответствии с дизайном нашего сайта. Часть своего ответа Вам разместила в другом комментарии.
Эти наблюдения занимают всего 3-5 минут несколько раз в месяц, и то далеко не в каждый. Необходимо только точно знать время и место наблюдения. Все, кто первый раз наблюдал (а многие даже не знают, что это возможно) искренне восхищаются, что можно увидеть невооруженным взглядом рукотворную яркую "звезду", да ещё и быстро движущуюся. Бывают моменты, когда светящаяся МКС ярче всех природных настоящих звезд на небе. Равнодушных не бывает.
На нашем сайте расчетами для наблюдения космической станции в Ульяновской области занимается ВИ0540 в своем проекте Наблюдение МКС. В Дубне время наблюдения мало различается от Ульяновска., только поправка на разницу часовых поясов. На мой взгляд, интересно наблюдать реальные траектории космических тел, особенно в сравнении с расчетными.
В который раз удивляюсь живучести сайта Лаборатория космических исследований УлГУ. Сайт был создан двумя аспирантами (научный руководитель Виктор Михайлович Журавлев) более 12 лет назад для общения внутри самой лаборатории. Тогда сайты только начинались создаваться, поэтому никаких амбициозных планов на длительную перспективу не планировалось. Не было опыта по ведению сайта, поэтому тематика складывалась естественным методом проб и ошибок. За эти годы сайт вели различные сотрудники лаборатории.
Сайт пережил несколько этапов подъёмов и спадов. И каждый раз, когда казалось, что сайт заканчивает свое существование (не было новых авторов и публикаций), в этот момент неожиданно появлялись новые участники, которые давали импульс жизнеспособности сайта. Число участников и просмотров страниц только увеличивается со временем: десятки стран и сотни различных городов по всему миру на всех континентах.
Талантливые творческие люди приходили на сайт и щедро делились своими идеями и проектами. Они все публиковали на нашем сайте свои знания и увлечения. Теперь новый участник сайта Георгий подхватил эстафету из рук нашего замечательного автора RMR_astra. Поразительно, что Георгий смог зарегистрироваться, когда уже не было свободной регистрации на сайте (только через личное обращение к админу сайта) и написал свой первый комментарий именно к статье RMR_astra. Мы только тогда узнали, что эта публикация набрала рекордное число просмотров и вернули ее на главную страницу сайта.
Уважаемая Полина!
С точки зрения механики продолжительномсть полёта МКС между коррекциями целиком и полностью определяется лишь силой аэродинамического сопротивления станции из-за наличия хотя и слабой, но присутствующей атмосферы. Учесть точно влияние сопротивления (коэффициент лобового сопротивления Cx(М), где М число Маха, равное Vорбит./a звука) можно либо при наличии точных аэродинамических продувок станции в сооответствующих сверхзвуковых трубах ЦАГИ, поскольку её форма весьма специфическая и представляет из себя больше летящую птицу с огромными боковыми солнечными панелями - крыльями, сильно влияющими на коэффициент сопротивления, либо просто эмпирически по величине потери орбитальной скорости полёта станции за заданный период времени, что гораздо проще и точнее.
Но от неизбежной потери скорости никуда не деться. Единственный выход - поднять дополнительно высоту высоту полёта станции над Землёй на пару сотен км в область ещё более разряженной атмосферы. Но сверху, как Вы прекрасно знаете, есть ограничение на попадание в область нижней границы пояса Ван-Аллена, в котором крутятся, подобно белке в беличьем колесе, высоко скоростные заряженные частицы, выброшенные Солнцем в виде солнечного ветра, которые сродни вредным фактором атомного взрыва и ничего хорошего не приносящими здоровью космонавтов на станции. Известно, что после сильных солнечных магнитных бурь радиоактивность в поясе возрастает на несколько порядков и держится месяцами на высовом уровне. Что является весьма жёстким ограничением на пилотируемые полёты в открытый космос. Поскольку при пересечении пояса в таком высокоактивном состоянии можно получить смертельную дозу радиации за одно пересечение этого пояса, толщина которого достигает порядка 1-1,5 тыс.км.(по памяти)) При этом надо выбирать особые траектории выхода и входа в пояс ближе к полюсам магнитного поля Земли, где его толщина минимальна.
Поскольку станция и так довольно высоко летает, то остаётся только доставлять периодически дополнительный запас топлива для поднятия орбиты станции за счёт включения двигателей самих пристыковавшихся "грузовиков".
Наблюдениями пролётов не занимаюсь, распределяю свободное время между работой в огороде (в летнее время) и увлечениями (радиолюбительством (собрал себе Hi-Fi усилитель мощности с малыми искажениями (0,002-0.02%), слушаю советскую эстраду и шедевры инструментальной и классической музыки, иногда фотографирую (Canon_SX-50 и FUJIFILM-S9600 - мегазумные компакты), люблю программировать, а в последнее время, увлёкся написанием комментариев, чему очень рад и благодарен Вашему сайту.
Желаю Вам здоровья и успехов в работе.
Георгий. 1.04.2020г 11час 38мин. Время моск.
Уважаемый Георгий!
Вы не проверяли траекторию МКС в соответствии с анализом механики движения? Двигатели на МКС, конечно, подправляют траекторию, но большую часть станция движется по законам механики.
И еще один вопрос. Вы наблюдаете пролеты МКС в своей местности?
Все пролеты обязательно постараемся понаблюдать - можно сказать, событие в режиме изоляции. Сейчас мы практически "на одной волне" с космонавтами на борту МКС.
А 20 мая 2020 года, наверное, будем жить в уже совершенно изменившихся, пока непредсказуемых условиях. Поживем- увидим.
Уважаемый zhvictorm!
Большое спасибо, что нашли время ответить на мою просьбу. Книгу Милюкова и Сагитова мне уже доводилось ранее читать как одну из немногих популярных на тему определения гравитации. А вот в Вашей новой ссылке обнаружил что-то мне не очень понятный отказ от измерения периода колебания крутильных весов и это при малозатухающих колебаниях с их перерегулированием! Как можно что-то тогда определить, по величине заброса что ли? Или они умудрились ввести неплохое демпфирующее усилие, гасящее перерегулирование. Изменение периода ведь понадёжнее будет. Не очень понятно. Главное, видимо,что притяжение между малыми массами всё-таки, видимо, есть (для меня это самое важное), если столько разных групп работает над этим вопросом. Просто мне хотелось сравнить, например, свои расчёты и экспериментальные данные в виде графика колебания маятника. Но видимо, не судьба. Кстати, на мой взгляд, неоправданно привлекать какие-либо виды электростатических полей, какими бы благими намерениями ни оправдывалось их введение, что бы случайно не перепутать их между собой, имеющими одинаковую обратно квадратическую зависимость. Ибо уже появились сторонники электростатической версии поисхождения силы гравитационного притяжения между телами.
Кстати, где-то читал, что сама сила гравитации не очень стабильна и слегка изменяется на больших промежутках времени (месяцы и годы), что , видимо и не позволяет добиться стабильности в измерениях. Все измерения на разных установках желательно было бы договориться проводить разным группам исследователей одновременно, что бы исключить этот неизвестный фактор влияния, видимо, из далёкого космоса, а может быть и не очень далёкого, а от Солнца. Неплохо было бы привлечь одновременный учёт результатов измерений гравитации Солнца по данным проекта "Паркер", если они , конечно, предусмотрены этой программой.
Ещё раз спасибо за информацию.
Георгий. 28.03.2020 23ч45м Время моск.
К вопросу о трёх основных законах Ньютона
Вернёмся ещё раз к трём законам Ньютона и рассмотрим их с точки зрения инженера-механика.
Перед первым законом Ньютон ввёл Определение III :
« Врождённая сила материи есть присущая ей способность сопротивления, по которой всякое отдельно взятое тело, поскольку оно предоставлено самому себе, удерживает своё состояние покоя или равномерного прямолинейного движения.»
Первый закон Ньютона
Для примера вариант текста Первого закона самого Ньютона из «Начал» в переводе А.Н. Крылова:
«Всякое тело продолжает пребывать в своём состоянии покоя или равномерного прямолинейного движения, пока приложенные силы не понудят его изменить это состояние».
Эта сила всегда пропорциональна массе, и если отличается от инерции массы, то разве только воззрением на неё. От инерции материи происходит, что всякое тело лишь с трудом выводится из своего покоя или движения. Поэтому «врождённая сила» могла бы быть весьма вразумительно названа «силою инерции». Эта сила проявляется телом единственно лишь, когда другая сила, к нему приложенная, производит изменение в его состоянии. Проявление этой силы может быть рассматриваемо двояко: и как сопротивление и как напор. Как сопротивление – поскольку тело противится действующей на него силе, стремясь сохранить своё состояние; как напор - поскольку то же тело, с трудом уступая силе сопротивляющегося ему препятствия, стремится изменить состояние этого препятствия. Сопротивление приписывается обыкновенно телам покоящимся, напор – телам движущимся. Но движение и покой, при обычном их рассмотрении, различаются лишь в отношении одного к другому, ибо не всегда находится в покое то, что таковым простому взгляду представляется.» Конец цитаты из «Начал».
Однако в Определении III и Законе не очень подчёркнута, на мой взгляд, очень важная особенность свойства инерции тела – её пропорциональность массе тела. По-моему, можно изложить первый закон, подчеркнув роль величины массы тела, хотя бы в следующем виде:
«Всякое материальное тело обладает свойством инерции, удерживающим его в состоянии покоя или равномерного прямолинейного движения. Сила, приложенная к телу для изменения этого состояния, испытывает сопротивление инерции тела, пропорциональное его массе.»
Однако, для доходчивости разъяснения Ньютон применил не совсем удачные с современной точки зрения термины «сила инерции» и «врождённая сила материи», введённые им с применением слова «сила», хотя из текста ясно, что на самом деле речь идёт о «врождённом СВОЙСТВЕ материи (массы)», а не силе, поскольку сила есть ВЕКТОР, обладающий направлением действия в пространстве, а вот «СВОЙСТВО ИНЕРЦИИ МАТЕРИИ (МАССЫ)» направлением не обладает и является величиной скалярной, а не векторной, и появляется во втором законе в виде скалярного множителя, обратно пропорционального величине массы тела, при пересчёте вектора воздействующей силы в вектор ускорения, вызванный этой силой и совпадающий по направлению с вектором действия силы. Как видим, свойство инертности массы тела является врождённым, скрытым от глаз и проявляющимся ТОЛЬКО в виде сопротивления при воздействии разгоняющей по скорости силы, или в виде напора при попытке замедлить скорость движения тела силой. Конечно же, Ньютон всё это прекрасно знал, но, видимо из удобства объяснения принятого в те времена применил термин «сила» вместо «свойство массы».
И если во времена Ньютона термин «сила» был вполне уместен для объяснения физики явления, то позднее, ситуация резко осложнилась после ввода в рассмотрение (для задач статики вместо динамики движении) Д’Аламбером и Эйлером разнообразных ФИКТИВНЫХ «СИЛ ИНЕРЦИИ» (для удобства расчётов в статике) путём как ОБМЕНА (ЗАМЕНЫ) РЕАЛЬНОГО УСКОРЕННОГО ДВИЖЕНИЯ тела НА ФИКТИВНУЮ СИЛУ, ПРИВОДЯЩУЮ К СТАТИЧНОЙ КАРТИНКЕ СО ВЗАИМНО УРАВНОВЕШЕННЫМИ СИЛАМИ, так и за счёт введения разных видов ФИКТИВНЫХ «СИЛ ИНЕРЦИИ», получаемых весьма простым путём формального умножения разных видов фиктивных ускорений движения тела в неинерциальных системах отсчёта на массу тела, что в соответствии со вторым законом равноценно появлению НОВЫХ фиктивных сил (со знаком минус перед ускорением!), действующих на тело, каких как «центробежные силы инерции», «кориолисова сила инерции» и т.п. За счёт таких ФИКТИВНИХ «СИЛ ИНЕРЦИИ» свойство инерции тела многие стали ошибочно отождествлять с этими силами, что по сути неправильно. Вспомним, что сам Ньютон применил термин «сила инерции», хотя это был синоним реального свойства тела сопротивляться воздействию приложенной к нему силы, а вовсе не фиктивная сила, введённая позже в неинерциальных системах вышеназванными учёными.
Этим тут же воспользоваись «любители реальности» фиктивных «сил инерции» в неинерциальных системах (см. критику книги А.А.Астахова в предыдущем комментарии), ссылаясь на вышерассмотренные термины «врождённая сила материи» и «сила инерции» у Ньютона в «Началах». На самом деле инерция тела проявляется не в виде ВЕКТОРНОЙ ФИКТИВНОЙ «СИЛЫ ИНЕРЦИИ», а в виде скалярного свойства ВЕЛИЧИНЫ МАССЫ тела, входящей во второй закон Ньютона при определении ускорения тела под воздействием результирующей силы, приложенной к телу для изменения его прежнего состояния. Многие забывают, что эти фиктивные «силы инерции» являются вторичными, не самостоятельными, а лишь являющимися ответной реакцией на активные центростремительное и переносное ускорения точек условного вращающегося твёрдого тела, которые ЧИСТО ВИЗУАЛЬНО приписываются от совпавшей в данный момент точки условного вращающегося твёрдого тела с рассматриваемым свободным телом БЕЗ РЕАЛЬНОГО ПРИЛОЖЕНИЯ К НЕМУ ПРИ ЭТОМ КАКИХ-ЛИБО СИЛ В НЕИНЕРЦИАЛЬНОЙ СИСТЕМЕ и поэтому их и надо просто ВЫЧЕСТЬ (т.е .прибавить со знаком МИНУС в виде уже фиктивных «антиускорений») из реального ускорения тела, рассчитанного под воздействием результирующей всех РЕАЛЬНЫХ сил приложенных к рассматриваемому телу для получений правильных расчётов динамики движения тела, а не умножать фиктивные ускорения на массу тела и плодить эти фиктивные силы в виде разных несуществующих «сил инерции».
В итоге, дело дошло до того, что многие поверили в РЕАЛЬНОСТЬ всех этих фиктивных «сил инерции», например, вполне серьёзно пытаются использовать фиктивную несуществующую центробежную силу для перемещения тела в направлении её действия от центра вращения, забывая о том, что это не самостоятельная сила, а лишь ответная реакция на центростремительную силу и стоит только убрать центростремительную силу, как, например, при раскручивании ядра легкоатлетом, то мгновенно пропадёт и центробежная сила как вторичная реакция вместе с центростремительной, а ядро полетит отнюдь не по радиусу вращения (как бы в направлении действия центробежной силы), а по нормали к радиусу вращения, т.е. по касательной к круговой траектории при одновременном пропадании обеих сил (центростремительной и как следствие пропадание центробежной) с накопленной окружной скоростью на момент отпускания ядра легкоатлетом.
Второй закон Ньютона
Этот центральный закон для расчёта динамики движения тел позволяет рассчитать величину ускорения движения тела при воздействии на него равнодействующей всех сил с учётом свойства инерции тела в виде его МАССЫ (описанного в первом Законе Ньютона), а затем и определить за счёт операции интегрирования проекций ускорения центра масс тела на оси выбранной системы отсчёта сначала составляющие проекций скорости, а за счёт интегрирования скоростей вычислить координаты, т.е. определить траекторию тела под воздействием равнодействующей всех сил, действующих на тело.
Эта задача расчёта динамики движения тела и была впервые сформулирована Ньютоном в «Началах» так же, как и обратная ей задача по определению ВЕЛИЧИНЫ результирующей силы, под действием которой сформировалась уже известная траектория движения тела, решаемая за счёт применения двойного дифференцирования траектории тела по времени.
Под силой в механике понимают всякую причину, изменяющую скорость тела.
Эти уравнения выведены при условии, что масса тела является постоянной величиной и независящей от скорости тела.
m * (dv/dt) = F; или, в другом виде: (dv/dt) = F / m; ……. (2.1)
m * (d2r/dt2) = F; или, в другом виде: (d2r/dt2 ) = F / m; ……. (2.2)
Величина F называется результирующей (геометрической суммой всех сил по правилу параллелограмма) силой, действующей на рассматриваемую материальную точку. Очевидно, что сила F является вектором (обладает направлением в пространстве), поскольку она равна производной вектора скорости по времени, или же второй производной от координаты тела.
Таким образом, в инерциальной системе отсчета производная от скорости (или ускорение) равна действующей на неё результирующей силе, отнесённой к массе тела. Это утверждение называется вторым законом Ньютона, а соответствующие ему уравнения — уравнениями движения материальной точки.
Прямое отношение ко второму Закону имеет Определение IV Ньютона о силах:
«Приложенная сила есть действие, производимое над телом, что бы изменить его состояние покоя или равномерного прямолинейного движения.»
Сила проявляется единственно только в действии, и по прекращении действия в теле не остаётся. Тело продолжает затем удерживать своё новое состояние вследствие одной только инерции. Происхождение приложенной силы может быть различное: от удара, от давления, от центростремительной силы.»
Кстати, в своих «Началах» Ньютон спокойно обошёлся без введения особых понятий об инерциальных и неинерциальных системах отсчёта, рассматривая лишь абсолютные и относительные движения материального тела, призывая лишь чётко разделять «истинные и кажущиеся движения»!
В связи общепринятым в учебниках принятым подчёркиванием необходимости обязательного наличия инерциальной системы для правильного выполнения второго закона. И даже такими , на мой взгляд, оскорбительными заявлениями о его якобы неработоспособности и неприменимости в неинерциальных системах, унижающими универсальность второго закона, хотелось бы просто сказать этим «интерпретаторам закона», что лучше бы они почитали «Начала» Ньютона, тогда может быть и поняли, что он все эти «проблемы второго закона» в неинерциальных системах отлично всё видел и призывал различать движение абсолютное и относительное (под коим он и понимал движение в неинерциальных системах), т.е. чётко видеть ускорения реальные (возникающие под воздействием реальных сил приложенных к рассматриваемому телу) и фиктивные (приписываемые телу без реального воздействия сил на него). Из-за отсутствия термина «ускорения» Ньютон их называл «истинные и кажущиеся движения». Давайте лучше почитаем самого Ньютона:
«Причины происхождения, которыми различаются истинные и кажущиеся движения, суть те силы, которые надо к телам приложить, чтобы произвести эти движения. Истинное абсолютное движение не может ни произойти, ни измениться иначе, как от действия сил, приложенных непосредственно к самому движущемуся телу, тогда как относительное движение тела может быть и произведено, и изменено без приложения сил к этому телу; достаточно, чтобы силы были приложены к телам, по отношению к которым это движение определяется.»
Как же ещё лучше и яснее можно было сообщить авторам учебников о том, для его грамотного применения в неинерциальных системах второго закона необходимо чётко ВИДЕТЬ И ОТДЕЛЯТЬ от «истинного движения ( от действия сил, приложенных непосредственно к самому движущемуся телу)» «кажущиеся движения (которое может быть и произведено, и изменено без приложения сил к этому телу (когда для этого достаточно того, чтобы силы были приложены к телам, по отношению к которым это движение определяется)».
Что мы, в итоге, и делаем при рассмотрении «сложного движения» в теоретической механике, вычитая из правой части второго закона все эти реальные ускорения условного вращающегося тела («по отношению к которому это движение определяется») уже в качестве «кажущихся ускорений» («антицентростремительного», «антипереносного» и «антикорилисова» ускорений), чисто визуально и без всякого на то основания приписываемых рассматриваемому свободному телу, на самом деле не имеющему никакой физической наложенной связи с этой произвольно вращающейся системой (в виде условного вращающегося твёрдого тела вместе с его осями неинерциальной системы). Так что Ньютон весьма недвусмысленно распространил область действия второго закона и на неинерциальные системы (относительные в его терминологии) и поэтому не надо писать о «неработоспособности второго закона в неинерциальных системах», а надо лишь правильно учесть в нём все виды фиктивных отрицательных «антиускорений», освобождающих свободное тело в неинерциальных системах от приписываемых ему реальных ускорений условного вращающегося твёрдого тела неинерциальной системы, как о том и писал Ньютон.
Так же не надо делать и неграмотных выводов о том, что первый закон якобы излишен и вытекает как частный случай из второго закона при нулевой величине равнодействующей силы, приложенной к телу, подразумевая этим его ненужность и избыточность при наличии второго закона. Надо просто понять, что ПЕРВЫЙ ЗАКОН ПРЕЖДЕ ВСЕГО ПОСТУЛИРУЕТ «ВРОЖДЁННОЕ СВОЙСТВО ЛЮБОГО МАТЕРИАЛЬНОГО ТЕЛА ОБЛАДАТЬ ИНЕРЦИЕЙ, ПРОПОРЦИОНАЛЬНОЙ ВЕЛИЧИНЕ МАССЫ ТЕЛА, приводящей к стремлению тела сохранять своё постоянное прямолинейное движение (или состояние покоя).
Поэтому в неинерциальной системе во втором законе необходимо из реального ускорения тела, возникшего под воздействием суммы всех реальных сил (гравитационных сил притяжения, и, например, силы тяги двигателя, аэродинамических боковых сил управления и силы сопротивления при наличии атмосферы и т.п.) вычесть сразу все фиктивные «антиускорения», незаслуженно приписанные свободному телу без всякого реального воздействия на него соответствующих сил и вызванные визуальным наложением собственного вращения и (или) ускоренного движения неинерциальной системы относительно свободного тела.
Кроме того надо иметь в виду, что к активным реальным силам могут быть добавлены силы, появляющиеся при наложении на свободное тело физических связей с вращающейся системой, как-то, например, сила трения при контакте тела (без проскальзывания) с поверхностью сообщит свободному телу все реальные ускорения вращающейся поверхности, и в частности, реальную «Силу Кориолиса» со знаком плюс перед кориолисовым ускорением (не путать с уже учтённым выше «антикориолисовым» ускорением со знаком минус), возникающая при наличии относительной скорости перемещения по вращающейся поверхности
В итоге будут получены значения во времени проекций относительного ускорения тела в неинерциальной системе, первый и второй интегралы от которых и позволят определить проекции скорости и координаты траектории (с учётом начальных условий по скорости и координатам тела).
Таким образом и решается, поставленная самим Ньютоном, задача расчёта динамики материального тела в классической механике с применением второго закона Ньютона независимо от применяемой системы отсчёта с обязательной необходимостью учёта особенностей появления ускорений формально приписываемых телу за счёт неинерционности системы отсчёта и которые необходимо вычитать в виде "антиускорений" из реального ускорения тела, полученного в результате воздействия на него равнодействующей всех реальных сил.
Третий закон Ньютона – Закон появления сил от взаимодействия тел.
В современной трактовке третий закон в учебниках формулиуется обычно следующим образом:
Силы взаимодействия двух материальных точек равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки.
При этом все забывают отметить расширенную трактовку Ньютоном всего многообразия возможных воздействий, сводя его лишь к давлению одного тела на другое. Первый и третий законы описывают два важных понятия в механике: свойство инерции тела в виде его массы и возможные источники появления самих сил, определеющие величину ускорения тела во втором законе механики. Авторство третьего закона признаётся бесспорным за самим Ньютоном и никем не оспаривалось.
Ньютон писал в «Началах» о всех возможных источниках появления силы:
« Происхождение приложенной силы может быть различное: от удара, от давления, от центростремительной силы.»
Поэтому у Ньютона, в отличие от современной трактовки его закона, смысл Третьего закона гораздо шире по видам взаимодействия между телами и он рассматривает ВСЕ ВОЗМОЖНЫЕ ВИДЫ ПОЯВЛЕНИЯ ПАРНЫХ СИЛ ЗА СЧЁТ ВЗАИМОДЕЙСТВИЯ ДВУХ МАТЕРИАЛЬНЫХ ТЕЛ и в нём идёт речь не только о равенстве сил при контакте двух взаимодействующих сил («от давления»), но и об обмене количеством движения между двумя взаимодействующими телами, например, как "при ударе тел" и даже с учётом их собственного вращения (см. теорию удара вращающихся тел в физике), а так же на расстоянии («от центростремительной силы») за счёт равных сил гравитационного притяжения в соответствии с законом взаимного притяжения («обратных квадратов»).
Вот изложение третьего закона у Ньютона с пояснениями к нему:
«Действию всегда есть равное противоположное противодействие, иначе – взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны.»
Если какое-нибудь тело, ударившись о другое тело, изменяет своею силою его количество движения на сколько-нибудь, то оно претерпит от силы второго тела в своём собственном количестве движения то же самое изменение, но обратно направленное, ибо давления этих тел друг на друга постоянно равны. От таких взаимодействий всегда происходят равные изменения не скоростей, а количеств движения, предполагая, конечно, что тела никаким другим усилиям не подвергаются. Изменения скоростей, происходящие также в противоположные стороны, будут пропорциональны массам тел, ибо количества движения получают равные изменения. Этот закон имеет место и для притяжений».
Рассмотрим подробнее это третий закон «для притяжений», исходя из того, что количество движения системы, состоящей, например, из двух тел равно произведению ПОЛНОЙ МАССЫ системы на СКОРОСТЬ ЕЁ ЦЕНТРА ИНЕРЦИИ, следует, что:
Q = m1 · V1 + m2 · V2 = (m1 + m2) · Vцентра системы = 0; (примем, например, что Vцентра системы =0)
И для неподвижного центра инерции двух тел получаем, что
m1 · V1 = - m2 · V2 , равенство количества движения относительно барцентра … (3.1)
что означает РАВЕНСТВО количества движения у двух взаимодействующих тел ОТНОСИТЕЛЬНО ИХ ОБЩЕГО ЦЕНТРА ИНЕРЦИИ (МАСС), знак минус свидетельствует о противоположной направленности векторов скоростей этих тел при их вращении вокруг общего центра инерции, который часто называют ещё и барцентром вращения взаимно притягивающичся тел. А поскольку вектора двух в каждый момент времени строго противоположны друг другу, то это означает, что тела вращаются с одной и той же угловой скоростью вращения ω относительно барцентра в противоположные стороны, поэтому можно заменить орбитальные скорости на выр.:
V1 = ω ·r1 и V2 = ω ·r2 , после их подстановки в выр. 3.1 и сокращения на скорость ω получим выр.(3.2) для моментов массы тел относительно барцентра, представляющие собой просто равенство моментов масс тела, равное обычному правилу моментов сил для рычага (для этого лишь достаточно умножить на одно и тоже значение гравитационного притяжения из закона взаимного притяжения (обратных квадратов) для этой пары тел):
m1 · r1 = - m2 · r2 ; равенство моментов массы относительно барцентра ……….(3.2)
Вы видите какие важные следствия вытекают из полной трактовки третьего закона для космических взаимно притягивающихся тел, позволяющие определить параметры их общего центра вращения (или центра инерции), т.е. барцентра, в котором и следует располагать начало систем координат для исследования движения взаимно притягивающихся космических тел, поскольку сам барцентр движется равномерно и прямолинейно или покоится, что существенно упрощает все выражения для ускорений движения рассматриваемых тел во втором законе.
На этом данная тема практически исчерпана.
P.S. Следующая, видимо не очень скорая, публикация будет посвящена светлой памяти RMR-astra, предложившей обратить внимание на тему рассмотрения устойчивости движения в либрационных точках Лагранжа (L1-L5). Возможно, будет создана и программа для расчёта пространственного движения тел в неинерциальной системе «Солнце - планета» для определения траекторий движения космических тел не только в областях, близким к либрационным точкам, но и для расчёта пролётных траекторий опасных для планеты астероидов.
Однако, до свидания и берегите себя от вирусов.
Георгий. 28.03.2020г. 22час.50мин. Время моск.
Уважаемый Георгий!
Постараюсь ответить на ваш вопрос. Эксперименты по измерению гравитационной постоянной проводятся до сих пор в разных странах. Эксперимент типа Кавендиша проводился, по крайней мере, лет десять-пятнадцать назад у нас где-то в Подмосковье. Такие эксперименты проводились в Китае, США и других странах. Вот пару ссылок на информацию об этих экспериментах:
1. Новые измерения гравитационной постоянной еще сильнее запутывают ситуацию
2. Гравитационная постоянная измерена новыми методами
В этих экспериментах измерения проводились для малых по массе телах, когда их массу можно точно контролировать. Проблема состоит в том, что разброс измерений оказывается слишком большим от эксперимента к эксперименту. Он чаще всего превышает приборную погрешность самих экспериментов. Доверительные интервалы не пересекаются. На следующей картинке (взятой из работы [ссылка 1] ) это показано очень наглядно:
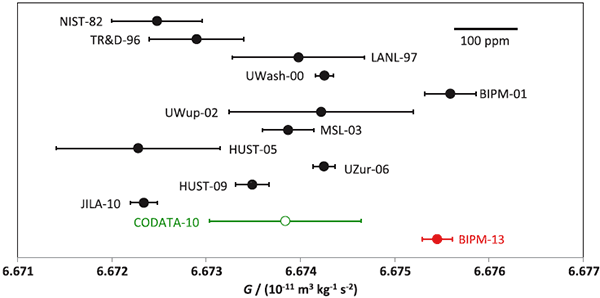
Это данные на 2013 год. К настоящему времени ситуация, насколько я знаю, не изменилась существенно. Подробности смотрите в [ссылка 1]. Это означает, что мы чего-то не знаем важного по поводу этой силы.
У меня на этот счет своя теория. Она изложена в моих работах по теории частиц. На сайте их можно найти. Другие предполагают, что дело в существовании дополнительной пятой силы. Но как видно из всевозможных экспериментов сила тяготения есть, и примерно такая, как это дается теорией тяготения Ньютона. Величина несколько меняется от каких-то не контролируемых условий эксперимента, но существует во всех экспериментах.
Кроме этого, есть гигантский набор астрономических наблюдений, который подтверждает наличие этой силы для газа и пыли, распределенных на пространстве в тысячи световых лет и больше. Друго дело, что концы с концами часто не сходятся. Это в первую очередь касается "темной материи". Большинство физиков и астрофизиков считают, что это некий тип материи. Эту материю ищут уже лет пятьдесят, а то и больше, но найти не могут. По моим представлениям, это изменение формы закона тяготения на больших масштабах, которые мы воспринимаем как дополнительную массу. Причем изменения формы тяготения не такие, как предсказывает ОТО. Но это, как говорится, другая история.
Дорогой Всеволод Иванович, конечно, мы искренне заинтересованы в Вашей информации.
Наблюдения за пролетами в прямом и переносном смысле приподнимают над низменным бытом. Пересматриваю статьи RMR_astra по этой же причине.
В настоящее время так важны истинные ценности. Космос в этом смысле - основа всей нашей жизни на Земле, наше прошлое и будущее.
Уважаемая Полина! Я ведь тоже винился перед Вами, что поздно передал эту заметку. .. Весь день постоянно переключался с одного дела на другое, часто напрасно тратя время.. Вот и протянул.. Как и вчера: пока очнулся и приготовил все бумажки,- МКС уже поднялся над горизонтом..Смысла отправлять сделанное уже не было...
Так что, Вы тут не причём.
Спасибо Вам, что Вы ещё проявляете интерес к моей инфомации.
Ждали наблюдения пролетов МКС, сработали, видимо, личные интересы.
Но, уважаемый ВИ0540, забыла выставить вовремя Ваше сообщение на главную страницу для тех, кто тоже хочет наблюдать яркую движущуюся "звездочку" в небе - МКС.
Уважаемый zhvictorm!
Прочитав впечатляющий список Ваших публикаций понял, что у Вас есть научные работы по теории гравитации. А меня как раз очень волнуют и интересуют вопросы реального подтверждения физическими опытами наличия гравитации между телами малой массы. С планетами всё ясно. А вот, есть ли у Вас ссылки на реальные современные данные, причём подробные, с реальными цифрами эксперимента (а не итоговые общие выводы), например, полученные на современных крутильных весах типа опыта Кавендиша по сериям опытов (с периодами колебаний весов, что меня в первую очередь и интересует, если, конечно, такие современные установки ещё существуют). Или данные других современных опытов, реально подверждающих наличие гравитации между телами с массами гораздо меньшими, чем у планет. А то меня как-то не устраивают отсылки на результаты опытов многовековой давности и всё равно без конкретных данных по измерениям. Где найти данные о фактических измерениях с применением современной техники, или это тоже "военная тайна", как и многое другое, скрываемое от общественности? Как-то наткнулся на описание современного опыта по измерению притяжения даже между атомами при их вертикальном падении в закрытом объёме, а вот чем всё это закончилось - незвестно.
В основе сомнений лежит, конечно же, статья некоего А.А.Гришаева (О.Х.Деревенский - это его псевдоним), сомневающегося в наличии гравитации между малыми телами.(http://newfiz.info/gra-opus.htm). После прочтения которой не поленился создать программу моделирования опыта Кавендиша со всеми размерами и массами его установки. В итоге получил данные о том, что при переводе притягивающих шаров из дальнего состояния в ближнее период колебания крутильных весов для установки Кавендиша должен увеличиваться почти ровно в ДВА РАЗА. Как, известно, но углу отклонения весов измерить притяжение не получается из-за малозатухающего колебательного поведения весов с периодом колебания до десятков минут. Так вот мои попытки найти подтверждающие аналогичные РЕАЛЬНЫЕ данные экспериментов на современных крутильных весах в интернете ни к чему не привели.
Как бы Вы кратко возразили А,А,Гришаеву, хотя бы просто ссылками на реальные измерения, а не на общие выводы типа "есть и точка"?
Георгий. 23.03.2020г 22с55м.Время моск.
О выводе геометрическим методом выражения для Кориолисова ускорения
Опишу непростой пройденный путь при попытке геометрического вывода формулы для кориолисова ускорения.
В предыдущем комментарии этот вывод легко и просто был произведён с применением чисто формального математического метода дифференцирования вектора относительной скорости, что лишь подтверждает всю мощь математического аппарата векторной алгебры, а именно:
Wс = (2ω × Vr). ………………………………………………………………….. (1)
В основу геометрического подтверждения этого выражения для реального ускорения Кориолиса было решено положить метод доказательства от уже заранее известного выражения к его геометрическому обоснованию и подтверждению вплоть до коэффициента 2 в выр.(1).
Итак, допустим, что нам известно конечное выражение сложной функции времени (f), которая является в первом приближении векторным произведением двух переменных Wc ~= f (ω × Vr). Найдём ее точное выражение геометрическим способом, применив для этого вывода правило для определения дифференциала от произведения двух функций времени: как произведение дифференциала от первой функции на вторую плюс произведение первой функции на дифференциал от второй:
Δ (ω × Vr) = Δ (ω) × Vr + ω × Δ (Vr). …………………………………………… (2)
где: Δ(…) – операция сообщения допустимого для данной функции небольшого по величине приращения, от которого мы потом избавимся, поделив на соответствующее ему небольшое приращение времени Δ(t), и после устремления величины Δ(t) к нулю, заменим отношения приращений Δ(…)/Δ(t) на выражение для производной d(…)/d(t) от функции, которая и будет равна УСКОРЕНИЮ Кориолиса.
Для геометрического вывода на плоской вращающейся поверхности (с угловой скоростью ω) и тела, имеющего физическую связь с этой поверхностью (в виде трения без проскальзывания) и перемещающегося относительннеё в любом возможном направлении (с линейной скоростью Vr). Нам даже не понадобится геометрический рисунок по причине его элементарности в виде обычной окружности как годографа (от вращения по кругу) конца радиуса-вектора r (или его же эквивалента - вектора относительной скорости Vr с длиной вектора Vr Δ(t), равной длине вектора r ), описывающего эту самую окружность, а в центр этой окружности поставим вертикальный кол в виде вектора угловой скорости вращения (вектор ω, вращающийся для определённости с положительной угловой скоростью, т.е. против часовой стрелки). Вот и вся заготовка для мысленного рисунка.
С начала была предпринята довольно быстрая и успешная попытка с применением вышеописанного правила сложения двух независимых приращений по ω и Vr для геометрического обоснования выр.(1) в случае, когда вектор скорости Vr был направлен вдоль радиуса-вектора дальности (R большое) из центра вращения плоской поверхности, расположенного, где-то внизу плоскости рисунка, т.е. вне вышеописанного малого круга (с малым радиусом r). Не буду его описывать сам вывод, т.к. это будет сделано позже на примере малого круга с радиусом r. Метод реализовался легко и просто, т.е. в случае направления относительной скорости тела Vr вдоль радиуса-вектора дальности (R большое) никаких проблем не возникло.
Но когда была предпринята аналогичная попытка вывода выражения тем же самым способом, но только случае, когда вектор скорости Vr, направлен перпендикулярно к радиусу-вектору дальности (R большое) вывод застопорился и никак не поддавался. То, что элементарно и очевидно срабатывало в первом случае наповал не срабатывало во втором случае тангенциальной скорости по отношению к радиусу-вектору (R большое) из центра вращения.
И тут пришло озарение, состоящее в том, что вектор скорости вращения подстилающей плоской поверхности ω надо перенести из своего истинного центра вращения подстилающей поверхности в центр масс самого движущегося с линейной скоростью Vr тела! Ведь мы так фактически и поступаем, когда применяем правило правой руки для определения векторного произведения, совмещая в одну точку вектора угловой и линейной скоростей!
Вот тогда геометрический вывод подтверждается на круге малого радиуса r с его центром в самой подвижной рассматриваемой точки даже независимо от направления вектора скорости Vr в силу полной круговой симметрии самого малого вращающегося круга, из центра которого и направлен вектор относительной скорости перемещающегося по поверхности тела.
Предпосылкой для такого действия переноса вектора вращения ω явилась и сама методика простого вывода по первому удачному варианту геометрического вывода, когда Vr был направлен ВДОЛЬ большого вектора-радиуса R вращения тела, проведённого из далёкого истинного центра вращения поверхности. Тогда при выводе одной из равноценных составляющих формулы, равной (Δ (ω) × Vr), получаемой ТОЛЬКО ЗА СЧЁТ ПРИРАЩЕНИЯ по угловой скорости (Δ (ω)) приходилось брать разницу В ДЛИНАХ ПУТЕЙ, ПРОХОДИМЫХ ПРИ ВРАЩЕНИИ ПО КРУГУ ЦЕНТРОМ МАСС ДВИЖУЩЕГОСЯ ТЕЛА, И КОНЦОМ ЕГО ЖЕ ВЕКТОРА ОТНОСИТЕЛЬНОЙ СКОРОСТИ, ОТСТОЯЩИМ ОТ НЕГО ВПЕРЁД НА РАССТОЯНИЕ малого-радиуса вектора r и при этом за счёт ТОЛЬКО ДЛИНЫ САМОГО ВЕКТОРА r И ПОЯВЛЯЛОСЬ ПРИРАЩЕИЕ ЛИНЕЙНОЙ ГОРИЗОНТАЛЬНОЙ СКОРОСТИ КОНЦА ВЕКТОРА r ОТНОСИТЕЛЬНО НАЧАЛА САМОГО ВЕКТОРА, ВЫЗАННОЙ РАЗНИЦЕЙ В ЛИНЕЙНЫХ СКОРОСТЯХ ВРАЩЕНИЯ ПОДСТИЛАЮЩЕЙ ПОВЕРХНОСТИ (на базе длины вектора малого вектора r ).
С учётом вышесказанного, осталось только произвести геометрический вывод выражения для корилисова ускорения по методике взятия дифференциала (приращения) от произведения по выр.(2), используя мысленный круг с малым радиусом-вектором r и его же эквивалента - вектора относительной скорости Vr с длиной вектора Vr Δ(t). Напомним правило для взятия дифференциала от произвеения двух функций времени:
Δ (ω × Vr) = (Δ (ω) × Vr) + (ω × Δ (Vr)). ………………………………………. (2)
Определим оба независимых приращения в правой части выр.2, считая, что первое приращение происходит только за счёт поворота вектора относительной скорости на небольшой угол, равный (ω Δ(t)) за счёт ТОЛЬКО ВРАЩЕНИЯ ПОДСТИЛАЮЩЕЙ ПОВЕРХНОСТИ. При этом нас интересует ТОЛЬКО ВРАЩАТЕЛЬНАЯ ЧАСТЬ ОТ ЭТОГО движения подстилающей поверхности, поскольку плоскопараллельноя поступательная часть этого движения подстилающей поверхностиникаких эффектов в виде ускорений не даёт и её можно НЕ РАССМАТРИВАТЬ, а вот это и означает, что вращение можно рассматривать относительно НАЧАЛА ЦЕНТРА МАСС ДВИЖУЩЕГОСЯ ТЕЛА в виде вектора вращения ω при радиусе-векторе r, полностью совпадающему, например, с вектором относительной скорости r = Vr и пока без его приращения по времени.
Тогда, раскрывая векторное первый член приращения в выр. (2), т.е. произведение Δ (ω) × Vr, получим вектор дополнительной линейной скорости ΔVr, конца вектора Vr, возникаюший при повороте конца вектора Vr в горизонтальной плоскости подстилающей поверхности с угловой скоростью ω, и это лежащий вектор приращения скорости (ΔVr) в горизонтальной плоскости расположен нормально к концу радиуса-вектора вращения r и представляет собой аналог вектора окружной скорости конца радиуса-вектора при равномерном вращении по кругу, т.е.:
ΔVr1 = (Δ(ω) × Vr) = (ω Δ(t) × Vr) = (ω × Vr) Δ(t). …………..…….………….(3)
Вторую составляющую в выр.(2) получим за счёт другого приращения (независимого от первого) по смещению вперёд (относительно центра рассматриваемого нами круга) самого вектора скорости линейной Vr вдоль самого себя на малое расстояние, равное приращению пути за период времени Δ(t), т.е. Δ (Vr) = Vr Δ(t) и которое сопровождается появлением дополнительного приращения боковой линейной скорости конца вектора относительной скорости ТОЛЬКО ИЗ-ЗА ПРИРОСТА РАДИУСА ВРАЩЕНИЯ на величину Vr Δ(t), поскольку возрастает скорость вращения подстилающей поверхности за счёт смещения целиком самого вектора относительной скорости Vr на приращение величиной, равной Δ (Vr) = Vr Δ(t). По правилу раскрытия векторного произведения получим вторую составляющую кориолисова ускорения в виде:
ΔVr2 = (ω × Δ(Vr) = (ω × Vr Δ(t)) = (ω × Vr) Δ(t). …………………………. (4)
Просуммируем оба коллинеарных вектора приращений из выр.(3 и 4) , направленных в одну сторону, влево по нормали к концу вектора скорости Vr, в соответствии с выр.(2) для взятия дифференциала:
ΔVr полн. = ΔVr1 + ΔVr2 = (ω × Vr) Δ(t) + (ω × Vr) Δ(t) = (2ω × Vr) Δ(t). …... (5)
Поделив обе части выр.(5) на Δ(t) и взяв предельный переход за счёт устремления Δ(t) к нулю, получим окончательное выражение для кориолисова ускорения, совпавшее с выр.(1), полученным ранее с применением методов векторной алгебры:
Wc = Lim| Δ(t) ->0 (ΔVr / Δ(t)) = (2ω × Vr). ….……………………………………..(6)
Вот так, совершенно просто (даже без реального, а лишь воображаемого рисунка!), удалось геометрическим способом получить правильное выражение для Корилисова ускорения с учётом правила взятия дифференциала от некоего исходного векторного произведения двух параметров (ω,Vr) для тела перемещающегося над вращающейся поверхностью при полной независимости выр.(6) от направления вектора относительной скорости по направлению относительно подстилающей поверхности.
И ВСЁ-ТАКИ ЦИФРА ДВОЙКА (2) В КОРИОЛИСОВОМ УСКОРЕНИИ НЕОБХОДИМА И ЕЁ ВЕЛИЧИНА НИКАК НЕ ЗАВИСИТ ОТ НАПРАВЛЕНИЯ ВЕКТОРА ОТНОСИТЕЛЬНОЙ СКОРОСТИ ТЕЛА по отношению к подстилающей вращающейся поверхности.
Поэтому все попытки некоторых авторов доказать переменность числового коэффициента (2) перед вектором угловой скорости ω в выражении (6) для Кориолисова ускорения или замену 2 на 1 , с моей скромной точки зрения, АБСОЛЮТНО НЕСОСТОЯТЕЛЬНЫ и демонстрируют лишь их многочисленные заблуждения и наукообразные плутания в попытке обосновать другие значения коэффициента при ω на примере многочисленных и малопонятных стереометрических рисунков.
Вот, например, некий автор А.А.Астахов, посвятил этой проблеме целую книгу, основная часть которой и была посвящена анализу кориолисова ускорения. (http://www.sciteclibrary.ru/texsts/rus/stat/st5379.pdf ).
В аннотации к статье автор пишет:
«Точное значение силы Кориолиса не равно удвоенному произведению угловой скорости переносного вращения на линейную скорость относительного радиального движения. Численный коэффициент в этом произведении всегда меньше двойки. Отличие тем больше, чем меньше радиус переносного движения. С увеличением радиуса переносного вращения коэффициент стремится к двум. Ускорение Кориолиса, определяющее геометрическое приращение поворотного движения равно половине классического ускорения Кориолиса. При равномерном относительном движении перпендикулярном радиусу сила и ускорение Кориолиса не проявляются.»
Как видим, автор не догадался перенести вектор вращения в центр масс движущегося тела (что можно и надо делать обязательно в полном соответствии с правилом раскрытия векторного произведения (2ω × Vr) ) и он, как и я в начале, утонул в дебрях «движения, перпендикулярному радиусу-вектору, проведённому из центра вращения в центра масс тела».
При этом попутно автор, видимо, не хочет говорить (а скорее и не подозревает) о возможности существования реальной "Силы Кориолиса", определяемой по выражению: Fкор = (2ω × Vr) m. Именно реальным воздействием которой и объясняются эффекты подмывания правых берегов у всех рек северного полушария Земли независимо от направления течения, а также закручивание атмосферных циклонов во вращение против часовой стрелки (см. предыдущий комментария от 16.03.2020.)).
В качестве подтверждения другого моего предложения о необходимости УСТРАНЕНИЯ из механики ВСЕХ ФИКТИВНЫХ «СИЛ ИНЕРЦИИ», к коим и относится незаслуженно упоминаемая во многих учебниках ОТРИЦАТЕЛЬНОЕ И ПОЛНОСТЬЮ ФИКТИВНОЕ (подчёркнуто для А.А.Астахова) Кориолисова сила инерции (Jкор.= – (2ω × Vr)m) было предложено ОТКАЗАТЬСЯ ОТ ВСЕХ ФИКТИВНЫХ СИЛ, ОСТАВИВ ВМЕСТО НИХ В НЕИНЕРЦИАЛЬНЫХ ВРАЩАЮЩИХСЯ СИСТЕМАХ ЛИШЬ ИХ ФИКТИВНЫЕ «АНТИУСКОРЕНИЯ» (например, «антикориолисовое»: Wантикор.= – (2ω × Vr)).
И вот этому очередное наглядное подтверждение из книги этого автора в виде цитаты из его статьи, (извините за длинную цитату):
«И в геометрических, и в аналитических выводах ускорения Кориолиса во всех современных учебниках, а также в работах классиков теоретической механики фигурирует удвоенное именно геометрическое, т.е. реальное ускоренное приращение траектории поворотного движения в направлении линейной скорости переносного движения. Примеров этому в нашей работе приведено достаточно много. И самый яркий из них по представлению физической сущности классической версии явления Кориолиса это определение удвоенного ускорения Кориолиса, как линейного ускорения через линейный путь, пройденный с ускорением Кориолиса.
Такие выводы есть, в том числе и в справочной литературе по физике. Причём в них не оговаривается, что это ускорение фиктивное.*1)
Фиктивной, по мнению классической физики, является лишь сила Кориолиса.*2)
Причём не половина силы Кориолиса, а именно вся её физическая величина...
Более того, ошибка определения ускорения поворотного движения прочно вошла в математический метод дифференцирования криволинейного движения по приращению его координат. Приращение скорости это всегда приращение расстояния, пройденного с ускорением, но приращение координат не всегда соответствует приращению этого расстояния. Поэтому вторая производная от приращения координат не всегда соответствует реальному геометрическому ускорению криволинейного движения. Классическое дифференцирование приращения криволинейного движения этого не учитывает.»
*1) К вашему сведению, это ускорение и есть самое настоящее реальное (а не фиктивное, как вам кажется), т.е.реальное ускорение точек условного твёрдого вращающегося тела со знаком плюс, а не фиктивное со знаком МИНУС, вводимое в уравнения в неинерциальной системе для устранения несправедливо и чисто визуально наложенному на свободное тело, которое никакими физическими связями не привязано в точкам вращающегося условного тела!
*2) Это так называемая «сила Кориолиса инерции». И не надо путать двух разных «баранов»: ранее названную полностью фиктивную «сила Кориолиса инерции» (со знаком МИНУС) и просто «Силу Кориолиса» (без добавления слова «инерции» и со знаком ПЛЮС), которая вполне реальна и о существовании которой автор даже не догадывается, возясь по-прежнему с официальной (из учебников) отрицательной по знаку и фиктивной «силой Кориолиса инерции» и которую он ещё и вдобавок УСЛОВНО разделил на две части (вдоль радиуса вектора и поперёк него), усмотрев в первой из них реальность, а во второй, с выводом выражения для которой он так и не смог справиться, – фиктивность. С чем мы его и поздравляем. Именно в этом-то и небольшом отличии в названии двух Сил Кориолиса и состоит грубая ошибка автора, не различившего две разных противоположно направленных силы: фиктивную "Силу Кориолиса инерции"(отрицательную по знаку) и реальную "Силу Кориолиса"(положительную по знаку).
Вот так от мешанины из ДВУХ СОВЕРШЕННО РАЗНЫХ ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫХ СИЛ Кориолиса, превратившихся для автора статьи в одну единую «фиктивную и наполовину реальную» НОВУЮ гибридную Силу Кориолиса, чудесным образом совместившей в себе фиктивную «Кориолисову силу инерции» СО ЗНАКОМ МИНУС (на слово «инерции» в учебниках все уже давно как-то перестали обращать внимание) и опрометчиво введённой в учебниках (видимо, для того, чтобы всех запутать окончательно букетами из разнообразных «Сил инерции»), и вполне реальную Силой Кориолиса (без ключевого слова «инерции» И СО ЗНАКОМ ПЛЮС перед тем же самим реальным кориолисовым ускорением), возникающей вполне реально при наличии физических связей с вращающейся поверхностью Земли (например, при подмывании одного из берегов рек и эффект закручивания циклонов в вихри). Автор, не разобравшись с этими двумя АНТИПОДАМИ из двух Сил Кориолиса противоположно направленными (причём одна из них фиктивная, а другая реальная), перевалил со своей «больной головы» на «здоровую голову» математики все свои проблемы вывода, бросив тень на метод дифференцирования (видите ли он «не всегда соответствует» ожиданиям автора). Надо же найти виноватого, вот он и найден в виде метода дифференцирования.
Надеюсь, молодёжи ещё более стал понятен предлагаемый мною принцип «ликвидации как класса» целого «зоопарка» «Сил инерции» (так любезных Астахову, что он за них «горой» против всех и вся, и даже начинает их считать вполне реальными!), и которым предлагается объявить их тотальную ликвидацию и подвергнуть наказанию в виде «пожизненного цика на гвоздях», как во второй серии фильма «Кин-дза-дза»*), не в меру расплодившихся на страницах учебников механики, и как следствие, необходимо одновременное ЗАКРЕПЛЕНИЕ ЗА ФИКТИВНЫМИ УСКОРЕНИЯМИ (как первоисточника всех этих бед в виде "Сил инерции") вполне почётного и заслуженного звания «АНТИУСКОРЕНИЯ» (в данном случае - «антикорилисова ускорения» со знаком МИНУС: Wантикор.= – (2ω × Vr)) и "антипереносное" ускорение (Wантипер. – также со знаком минус (относительно реального переносного ускорения точек твёрдого тела идущих вседа со знаком плюс) в неинерциальных вращающихся системах для нормальной работы второго Закона Ньютона при расчёте движения свободного тела.
*) Примечание, для разрядки атмосферы, немного о моём любимом фильме Г.Данелии: «Кин-дза-дза». Редактор MS Word всё упорно пытался заменить мои прописные буквы слова «цик» на заглавные «ЦИК», так же как и обратно прочитанное слово «кц» (обычные спички в фильме), т.е. «цк» на "ЦК". Ай да Георгий Данелия, не зря переписывал несколько лет для обхода цензуры, свой сценарий, весивший со всеми вариантами 5 кг! Съёмки фильма в пустыне Каракум были тяжёлыми и многие не снявшиеся по разным причинам в этом фильме актёры (Вахтанг Кикабидзе, Леонид Ярмольник, Валентин Гафт), думаю не раз пожалели об этом, а вот Юрий Яковлев был готов сняться у Данелии хоть на Луне. Даже когда он лежал в больнице, то в ответ на неожиданное предложение от Данелии сняться в фильме и «Что надо уже сейчас начинать сниматься»), Яковлев ответил: «Хорошо, я завтра выйду!». Талантливый дуэт ещё болезненного на вид Юрия Яковлева и плутоватого, добродушного и надутого (от осознания своего высокого происхождения) Евгения Леонова украшает этот фильм, да и Станислав Любшин им под стать. По началу фильм (выход на экран в 1987г) многие не приняли и только по прошествии некоторого времени люди оценили эту притчу об убогой действительности общества с дифференциацией по цвету штанов (оранжевые в фильме и малиновые пиджаки в перестройку) Кстати, название фильму дал не грузин Данелия с его любимой травой Закавказья - кинзой, а совсем случайно «выдал» Евгений Леонов, когда к нему, раскачивающемуся в гамаке внутри прохладпного пепелаца (космического корабля, больше напоминающего конический чугунный литой летающий "сортир"), подсел Станислав Любшин и спросил, «что в порт-феле» у Леонова, то тот сначала раздумчиво повторил окончание последнего слова «Феле-феле-феле», а затем ответил : «Зелень, кинза» и давай распевать «Кин-дза-дза-дза…» Всю дорогу он пел, а название осталось»…Так исчез первоначальный вариант названия фильма: «Космическая пыль»… Это отрывок из статьи Марии Конюковой из журнала «Тайны СССР №3 за 2020г., стр 16-17».
Однако, продолжим в назидание молодёжи демонстрацию этих заблуждений А.А.Астахова и приведём ещё одну фразу из рассматриваемой статьи, где автор обнаружил противоречия в Кориолисовой силе, которую он, видимо, знает только в виде ОДНОГО ФИКТИВНОГО ВАРИАНТА и даже не замечает знака ПЛЮС в реальной Кориолисовой силе ( а не фиктивной Кориолисовой силы инерции, кроме которой автор ничего не знает), когда в примере известного физика Фейнмана с движением человека по радиусу вращающейся карусели и испытывающего на себе воздействие вполне реальной силы Кориолиса вынужден наклоняться вбок для компенсации «закручивающуей силы», чтобы не упасть. Оцените всю глубину искреннего недоумения автора по этому поводу:
«Начнем с того, что выясним, почему закручивающую силу, которая реально изменяет угловой момент вращательного движения, Фейнман ассоциирует с силой Кориолиса, которая с точки зрения классической физики, являясь силой фиктивной, не может изменить момент импульса в принципе.
Фейнман пишет: ≪В действительности мы хотели бы узнать, какую боковую силу должен прилагать человек, чтобы двигать массу m со скоростью Vr=dr/dt. Как видите, она равна Fк = 2ωVr m ≫.
Фактически это означает, что двигая что-то по радиусу необходимо подстраиваться под вращающуюся систему, синхронизируя вращение движущегося вдоль радиуса тела с исходным переносным вращением за счет ≪обычной≫внешней боковой силы. В классической же физике «Сила Кориолиса» считается ФИКТИВНОЙ СИЛОЙ ИНЕРЦИИ. *)
Таким образом, Фейнман в своем выводе фактически противоречит самому себе и классической физике, определяя силу Кориолиса как реальную силу, поддерживающую переносное вращение движущегося радиально тела с исходной угловой скоростью, чтобы его вращение при радиальном движении соответствовало бы прежнему переносному вращению. И это противоречие вполне оправдано, т.к. это есть объективная реальность, которую не могут игнорировать даже сторонники классической модели поворотного движения.»
*) В классической физике ФИКТИВНОЙ СИЛОЙ ИНЕРЦИИ является не «Сила Кориолиса», , а «Сила Кориолиса ИНЕРЦИИ» (со знаком МИНУС!), фиктивная и направленная в обратную сторону по отношению к вполне реальному кориолисову ускорению (а заодно и к реальной "Силе Кориолиса")
Поэтому противоречит классической физике не Фейнман , а Вы, товарищ А.А. Астахов, не заметив как знака плюс в выражении Фейнмана (Fк= 2ωVr m.), так и невнимательно прочитав название силы: "Сила Королиса", но отнюдь не "Сила Кориолиса ИНЕРЦИИ". Хотя в вашем понятии, кроме фиктивной силы Кориолиса другой кориолисовой силы быть и не может!
Вот так А.А.Астахов, автор книги, посвящённой, в основном, анализу кориолисова ускорения вообще не знает и даже не догадывается о возможном существовании другой, реальной "Силы Кориолиса" (но не «инерции») .
А откуда тогда, разрешите спросить его, берётся реальное подмывание правых берегов рек и закручивание циклонов против часов в северном полушарии разве от фиктивной «Силы Кориолиса инерции»? Конечно же НЕТ, не от неё, а от реальной "Силы Кориолиса" со знаком плюс перед кориолисовым ускорением и с направлением действия в левую сторону (в северном полушарии) от направления скрости относительного движения, поворачивая вектор относительной скорости в плоскости вращающейся поверхности Земли всё время по нормали ВЛЕВО от направления вектора относительного движения.
Вот теперь, дорогой читатель, и оцените всю реальную и назревшую необходимость предложенной выше мною реформы в терминологии СИЛ И УСКОРЕНИЙ (см. мой комментарий от 16.03.2020г), если такой вполне себе нагловатый и считающий себя непогрешимым, автор, позволяющий себе критиковать ВСЕХ И ВСЯ, не взирая на лица и звания, ( и даже операцию дифференцирования умудрился между делом упрекнуть в неточнсти ) элементарно запутался в четырёх соснах из двух взаимно противоположных по направлениям Кориолисовых ускорений (реального и фиктивного, со знаком минус) и двух Сил Кориолиса (реальной и фиктивной с обязательным словом в названии «инерции» и со знаком минус перед ускорением)!
Однако автор выпустил ещё и книгу под названием: Александр Астахов «Физика. Порядок вещей, или Осознание знаний. Книга 2», «Издательские решения», где продолжил эту тему о фактической Силе Кориолиса, выдав «на гора» ещё одного уродца в виде Силы «Кориолиса-Кеплера», как он её называет:
«Поскольку в классической динамике вращательного движения понятие об обычной истинной силе Кориолиса-Кеплера отсутствует, то в классической физике родилась самая странная сила не только из всех сил инерции, но и самая странная из всех обычных сил!!! Классическая сила Кориолиса это либо, полу фиктивная обычная сила, либо, полу обычная фиктивная сила. Недаром физики всех времён и народов, начиная со времён Кориолиса, до сих пор спорят, реальна ли сила Кориолиса или же это только иллюзорная сила инерции.»*)
*) Вместо того, чтобы сообразить и умножить РЕАЛЬНОЕ Кориолисово ускорение (точек условного твёрдого вращающегося тела) на массу тела и получить вполне реальную Силу Кориолиса ( Fкор.= (2ω × Vr) m), направленную противоположно "Силе Корилиса инерции" (Fкор.инерции= – (2ω × Vr) m), автор придумал новый гибрид: «силу Кориолиса-Кеплера», (видимо, с заменой множителя 2 на 1), испытывая трудности с геометрическим выводом для ускорения Кориолиса в тангенциальном (поперечном) направлении относительно радиуса-вектора. Знай наших…
Однако у меня к автору книги: «А.А.Астахов Физика Порядок вещей, или Осознание знаний. «Издательство», 2017г.» имеется совсем другой и особый счёт, ибо всё вышеизложенное о его взглядах можно было бы простить автору списать на ошибки и заблуждения, которые можно только отметить (кто из нас не заблуждается или не ошибается – нет таких (в том числе имею в виду прежде всего самого себя). И мой тон был бы совершенно другим в вышеизложенных строках по отношению к автору и более спокойным и выдержанным. Однако сделано это сознательно, покольку есть за что публично наказать.
А вот за другие «прегрешения» хотелось бы спросить уже с автора по «полной программе», поскольку уже с начальных страниц своего опуса, посвящённых разбору Сил инерции, он рьяно набросился на уважаемого мною доктора технических наук, профессора кафедры теоретической механики Нурбея Владимировича Гулиа, написавшего, на мой скромный взгляд прекрасную небольшую книгу под названием «ИНЕРЦИЯ» Издательство «НАУКА» Москва 1982г. 152 стр.» Под эгидой «Академия наук СССР» Серия «Наука и техничесий прогресс» , ответственным редактором которой был, известнейший в области механики, академик А.Ю.Ишлинский. И какая же муха укусила этого Астахова, написавшего всякие гадости про классические взгляды Нурбея Владимировича по вопросам механики. Да под каждым словом небольшой, но безупречной книги Гулиа «ИНЕРЦИЯ» я подпишусь без всяких оговорок, т.к. в ней дан великолепный исторический обзор понятия инерции от античной механики до теории относительности, кратко, но весомо и понятно, чего не могу сказать об опусе словообильного Астахова.
Вообще-то нападки на тексты популярных книг Н.В.Гулиа о механике, силах и инерции вызваны со стороны А.А.Астахова явным НЕСОВПАДЕНИЕМ его представления и Силах инерции с классическим походом к ним как к чисто фиктивным, твёрдо проводимым и известным академиком А.Ю.Ишлинским, А вот для Астахова Силы инерции с одной стороны,чтобы не придпрались к нему, для него фиктивны, но чисто формально (как бы на словах), а с другой, гораздо большей, он считает их, как ни странно, вполне существующими и где-то даже реальными! И главное при этом, что он вместо того, чтобы все появления инертности в механике объяснять врождённым СКАЛЯРНЫМ СВОЙСТОВМ ИНЕРЦИИ МАССЫ ТЕЛА , заменяет для себя существованием почти реальных для него ВЕКТОРНЫХ НЕСУЩЕСТВУЮЩИХ И ФИКТИВНЫХ СИЛ ИНЕРЦИИ с радостью подхватив слова Ньютона в "Врождённой силе материи" при объяснении СВОЙСТВА ИНЕРТНОСТИ ТЕЛА. Такой вот эклектизм в одной голове в отношении к Силам инерции!
И как только он не называет Н.В.Гулиа: и «ярым сторонником фиктивности сил инерции» и что «слова Гулиа ( «…Сил инерции нет, не было и не может быть, потому что в существующей механике им места нет») - это логика типа: этого не может быть, потому что не может быть никогда. Может быть, профессор имел в виду не саму реальную действительность, а ее математическое описание?» и «высказывание Гулиа, скорее всего, следует понимать, как полное отрицание сил инерции в реальной природе».*)
*)Моё примечание: А как же может быть иначе иначе, если они и есть самые что ни на есть фиктивные в неинерциальных системах!
А на примере рассмотрения вращения Луны вокруг Земли дело дошло даже до смешного: Гулиа утверждает, что центробежная сила НЕ ПРИЛОЖЕНА к Луне, естественно, рассматривая её вращение в инерциальной невращающейся системе относительно центра масс Земли, а автор возражает ему следующим перлом, даже не разобравшись в какой системе отсчёта идёт анализ вращения (да, в неинерциальной земной системе к Луне вынужденно приложено ФИКТИВНОЕ «центробежное ускорение» (или «антицентростремительное» ускорение), на что Астахов глубокомысленно возражает, даже не представляя себе разницу между системами отсчёта:
«А поскольку небесные тела реально подталкивает(?) друг к другу вполне материальное поле тяготения, но при этом они не падают друг на друга, то надо полагать, что они сопротивляются ему при помощи вполне реальной центробежной силы».*)
*) Примечание: А может быть, т. Астахов, от того что у Луны есть соотвествующая по величине орбитальная скорость, которая и не позволяет ей рухнуть на Землю! А не благодаря несуществующаей в реальной действительности ФИКТИВНОЙ ЦЕНРОБЕЖНОЙ СИЛЫ! Поищите-ка её в инерциальной системе: её там никогда и не было, кроме ЕДИНСТВЕННОЙ силы притяжения Луны к Земле! И вот благодаря наличию орбитальной скорости Луна, ПАДАЯ ВСЁ ВРЕМЯ на Землю под воздействием ЕДИНСТВЕННОЙ силы притяжения к Земле лишь РАЗВОРАЧИВАЕТ ПО НАПРАВЛЕНИЮ свой вектор орбитальной скорости успевая пролететь вбок, по касательной к радиусу-вектору, направленномк на Землю. , что и приводит к эллипитческой орбите вокруг Земли (почти круговой). Не будет скрости и Луна прямиком, как сорвавшийся лифт, полетит прямо к Земле. Это вам для ОСОЗНАНИЯ и соотвественно для вашего ПРОСВЕТЛЕНИЯ.
Или вот эта наглость зазанавшегося и непогрешимого, а на деле безграмотного автора:
«Как можно утверждать, что он (Гулиа) всё и всем доказал, если с другой стороны можно со сто процентной уверенностью сказать, что сам Гулиа ничего толком не знает о природе инерции. И это не голословное утверждение. На сегодняшний день природа инерции официальной наукой, приверженцем которой является Гулиа, не установлена. Не известны и революционные работы самого Гулиа о природе инерции. Все его нынешние доводы не выходят за рамки средней школы.» *)
*) Природу инерции можно и не знать! Достаточно её лишь привильно учитывать, но грамотно, без вывиха в мозгах.! А по-моему скромному мнению, Вы сами и есть полное невежество и ничтожество, мнящее из себя знатока механики. Позор на уровне средней школы. Далее не буду продолжать, вполне хватит вышесказанного. Это у Вас самого , товарищ Астахов, знания не выходят за рамки средней школы!
И всё это о Докторе технических наук, участвующему в разработке оригинальных накопителей кинетической энергии для транспорта (http://nt.ru54.com/ac/gnv/index.html ) и супервариаторе для них (http://n-t.ru/tp/ts/sv.htm).
P.S. Уважаемый А.А.Астахов! Не надо ничего писать на данный сайт, ответа не будет. Поскольку я стою на страже научности данного сайта (выполняю общественное поручение), то Ваше присутствие на нём объявляю «persona non grata» …
А Вам не кажется, что надо бы извиниться перед уважаемыми людьми (перед Н.В.Гулия, например), что несколько пробудит Вашу подуснувшую совесть и загладит ошибки и заблуждения. Отталкивайтесь, пожалуйста, "от осознания и просветления" (по В.Высоцкому). Вот мне, например, хоть и стыдно за мои ошибки и несдержанности, допущенные мною на этом сайте, но нахожу же я в себе силу признать их. Поверьте, все ошибаются - это естественно, а у Вас, честно говоря, есть талант и глубокое мышление, но Вас одолевает гордыня, разрешающая Вам без огляки верить в Вашу непогрешимость и нападать на всех и вся. Боритесь с неправильными идеями, а не с людьми их высказавшими. После того, что Вы узнали о своих заблуждениях, главное сделать правильные выводя для себя и начать с раскаяния. Но не все могут побороть в себе этот самый страшный грех падшего человека - СОБСТВЕННУЮ ГОРДЫНЮ. Если Вы её сейчас преодолеете, не сделаете первый шаг и не раскаетесь, то она сожрёт Вашу бессмертную душу и погубит Вас окончательно... Вспомните последние годы Л.Толстого, его гордыню. Одумайтесь, пока не поздно, покайтесь. И с новыми силами принимайтесь за новые работы, только без наскоков на других и никогда не забывайте о слабости нашего ума, не возгордитесь, иначе - конец личности. Будьте благоразумны...
P.S. Следующий комментария будет о трактовке трёх законов Ньютона.
Георгий 21.03.2020г 23ч25мин.
Удивительное дело!
Луна не уходит к Солнцу, летает вокруг Земли - а ей упорно приписывают траекторию околосолнечную. Почему в таком случае спутникам Марса не приписывают подобные траектории. или Юпитерианским?
Есть система Земля-Луна, и она входит в систему Солнечную, как и все остальные планеты. И пора уж это понять и принять.
Другое дело. что Луна идет вокруг Земли несколько необычно, захватывая две разрешенные орбиты - да. Напоминая траекторию кометы. Но связано это скорее всего с тем, что ее диаметр больше, чем ширина максимальной разрешенной орбиты - 400000х0,005 = 2000км.
Ох, друзья, простите! Оказывается, я невнимательна - и к другим планетам и их спутникам применяют эту теорию. Слушайте, да вы эзотерики еще те!
Как может планета, у которой притяжение ниже, чем Солнечное, что-то удерживать около себя? Если Солнце тянет к себе Луну вдвое сильнее, чем Земля - то луна давно уже должна была у бежать от нас.
Ещё в старших классах школы соседка по дому, зная мой интерес к звёздам, пригласила меня на занятия астрономического кружка студентов Пединститута, который вела там Рахиль Менашевна.
С той поры во многих моих астрономических наблюдениях и исследованиях присутствуют руководство и участие Рахиль Менашевны.
Это и наблюдения затмений (в т..ч. - солнечного в Шортанды 30 мая 1965 г.), переменных звёзд, покрытий звёзд Луной, затмений спутников Юпитера и др. по программам ВАГО. И, конечно, первых ИСЗ, когда она стала начальником Станции визуальных наблюдений в Ульяновске. Её фото за приёмом "бип-бип"-сигналов первого в мире ИСЗ вы и видите в заголовке статьи о ней.
Со временем Р.М. доверила мне самостоятельно пользоваться телескопом УГПИ, бинокулярами и др. приборами станции наряду с ответственным за это Голобородько Е.И.
Читала статьи RMR_astra на сайте, они заставляли задуматься.
Светлая память.
И неожиданно приятно снова видеть знакомое красивое имя RMR_astra у автора комментария.
Благодаря этому сайту, возможности писать и быть читаемой, у Рахили Менашевны был смысл и способ существования последние 6 лет!
RMR теперь astra!..
Зеленцова Р.А., дочь Разник Р.М.