Вот! Это предельно важно, ИМХО.

Общаясь с учеными из самых различных сфер, я пришел к выводу, что в основе современной науки отсутствует целостная философская система. А без нее наука как без рук. Философия позитивизма себя исчерпала и скомрометировала еще в прошлом, если не сказать в позапрошлом веке. Коммунизм дал нам диамат. Но и тот не выдержал пробы временем. Сегодня же, по меткому выражению одного знакомого ученого, единственная философия науки это "tenure track", проще говоря, бабло.

А проблема тут вот в чем. Например, определие ЖИЗНИ как таковой, через "метаболизм" и т.п. слишком узко. Для материальных форм, возможно, это до некоторой степени приемлемо, да и то с оговорками. Но есть же еще и мета-физика. Не знаю, будете ли вы настаивать, что сознание - это функция материи, или все-таки согласитесь, что сознание - надматериально? А ведь это базовые вещи. Если относительно этого у нас нет ясной картины, то все остальные определения, которые мы выводим из этих первичных категорий, теряют смысл. 

В контексте планеты - нам важно определить, является ли планета живым организмом, или это всего лишь сгусток абстрактной материи, хаотическим образом самоорганизовавшийся из некоей протоматерии, которая досталась нам в наследство от БВ. Такой подход оставляет слишком много открытых вопросов, которые мы старательно пытаемся изолировать и не замечать. Например, а что же было за момент до БВ? ГДЕ происходит БВ? Почему он происходит? И т.д. Как насчет множественности БВ? Откуда у нас может быть уверенность, что тот БВ в поле которого живем мы, единственный во вселенной?

Современные ученые, судя даже по фильмам с того же Discovery channel, всё-таки готовы признать, что Земля - это живой организм. Не такой, как, скажем, человеческое тело, по форме и в деталях, но живой в том же смысле - обладающий собственным индивидуальным бытием. Всем очевидно, что человек создан из элементов Земли, но если Земля - это неживая материя, то как она может быть источником жизни? И если так, то значит источник жизни находится за пределами Земли? Где? Говорят, что "жизнь" на планету занесли "метеоры". Хорошо, но откуда? И там-то она откуда взялась? 

Для меня, например, очевидно, что именно Солнце "родило" планеты. И их спутники. Как - это уже другой вопрос. Вы же не станете спорить, что, как я уже говорил, именно Солнце является источником энергии (читай, жизни) нашей планеты и, в частности, всего, что находится на ее поверхности. Если Солнце "выключить" - планеты не будет. Ни Земли, ни Юпитера, ни Плутона, ни Луны, ни даже Цереры. Вся энергия, которой мы располагаем, приходит к нам от Солнца. Из нее сотканы все наши атомы, нейтроны, протоны, электроны и прочие "бозоны". Ну, может быть, что-то "долетает" и от других звезд, и даже из Центра галактики, но в основном, Солнце - это наше все. Солнце - это наша вода, это микроэлементы, это электромагнитное поле и т.д. Солнце - это основа жизни, даже если под "жизнью" Вы готовы признать исключительно материальные компоненты.

Тот факт, что СС организована определенным образом, а именно: эллипсы орбит, орбитальные скорости, наклоны осей вращения и самое осевое вращение планет - все это говорит о том, что в основе этого всего лежит некий стройный закон. Исходя из понимания именно этого факта, мы верим, что все звездные системы устроены одинаково, хотя мы никогда там не были и даже в "трубу" этого не видели. Этот закон нам не понятен до конца, но он точно есть, и все наши "научные гипотезы" - это попытки осмыслить этот закон, который существует до и помимо нашего понимания, независимо от него. Как планета существует до нашего рождения и, судя по всему, останется на орбите после нашей сметри (если мы своими руками не взорвем ее, конечно).

Солнечная система  - это именно организм: устроенный определенным образом, имеющий стройный вид. И планеты в нем играют роль "органов". То, что нам не понятна роль планет в жизни СС, говорит только об узости нашего кругозора и о нашем нежелании/неспособности признавать очевидные вещи.

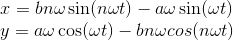
Т.е. Вы предлагаете принебречь массой Луны и ее собственным осевым вращением? Взять только расстояние до Солнца и (переменную) орбитальную скорость и расмотреть их векторное произведение? Орбиту Луны Вы тоже предлагаете "спрямить" до Земной?

Благодарю Тимофей Александрович! С Новым годом и Рождеством Христовым и Вас поздравляю. Всегда приятно с Вами пообщаться.

По поводу ереси не очень понимаю, что из приведенных выше цитат "оскорбляет" Ваши "чувства верующего". Разве не очевидно, что существует жесткая иерархия: галактика (центр галактики) - звездная система (звезда) - элемент звездной системы (планеты, спутники и т.п.). Разве есть соменения в том, что без Солнца не было бы и всей СС? Разве Луна в первую очередь не элемент СС, а после уж - спутник Земли? Очевидно ведь, что основным (если не сказать единтсвенным) источником энергии для планет (и их спутников) является звезда.

Вообще любопытно, что в данном контексте вы прибегаете к религиозной терминологии. Действительно, в последние годы наука приобретает множество сходных черт с религией: все больше положений науки приходится принимать на веру. Теория БВ, например.

По моменту импульса.

$\overline L=m \overline \rho \times \overline v$

Как перемножить векторы я, пожалуй, разберусь. Но чему они равны?

И. Правильно ли я понимаю, что мы тут ищем момент импульса Луны в гелиоцентрической системе отсчета?

Вот в википедии читаем:

"На орбите момент импульса распределяется между моментами импульса собственного вращения планеты и её орбитального движения:

$L_{total} = L_{spin} + L_{orbit}$"

В таком случае для Луны необходимо добавить еще один момент:

$L_{total} = L_{spin} + L_{orbit} + L_{dev}$

где $L_{dev}$ - момент импульса Луны в ее движении относительно орбиты Земли, в том смысле, что она не просто движется по орбите (солнечной), которая по сути совпадает с орбитой Земли, но также с известной периодичностью отклоняется от этой орбиты.

Из приведенной статьи видно, что если "эллипс возвести в квадрат", то он останется эллипсом, только фокус его сместится в центр. Это красиво, но мне как неспециалисту не очевидна связь эллиптичности орбит с законом обратных квадратов: "В физике закон обратных квадратов — это закон, утверждающий, что значение некоторой физической величины в данной точке пространства обратно пропорционально квадрату расстояния от источника поля, которое характеризует эта физическая величина." (Википедия). Честно сказать, тут очень много дополнительных вводных, типа "отрицательной полной энергии" и проч. Моих скудных знаний в данной области, увы, не хватает.

     Всё:  и погода, и место, и время , и яркость вспышки, и даже западный холодный ветер - всё прошло, как учили!  Ну, а насколько вспышка была ярче Веги: в 15, в 10 или 12 раз, - решайте сами.

С новым оборотом вокруг Солнца!

Пост я перенес выше. В начало.