Задача двух тел в теории движения Луны.
 При изучении небесной механики неизбежно возникает специфический вопрос: какое влияние на орбитальные характеристики оказывает масса тела? Для очень малых тел, движущихся вокруг большого центрального тела, их масса не имеет значения. Зато по периоду их обращения и большой полуоси их орбиты можно определить массу большого тела.
При изучении небесной механики неизбежно возникает специфический вопрос: какое влияние на орбитальные характеристики оказывает масса тела? Для очень малых тел, движущихся вокруг большого центрального тела, их масса не имеет значения. Зато по периоду их обращения и большой полуоси их орбиты можно определить массу большого тела.
Не так обстоят дела с телами, масса которых хоть сколько-нибудь сравнима с массой центрального тела. И в Солнечной системе такое тело есть. Это Луна. Она уникальна. В последние 400 лет именитые ученые оценивали ее массу значениями от 1/40 до 1/81 массы Земли.
Оказывается, относительное перемещение взаимно притягивающихся тел в создаваемом ими силовом поле можно описать уравнением движения для тела с массой, равной среднему гармоническому их масс1. При этом период обращения будет зависеть от суммы масс этих тел2.
Давайте посмотрим, откуда берется это среднее гармоническое.
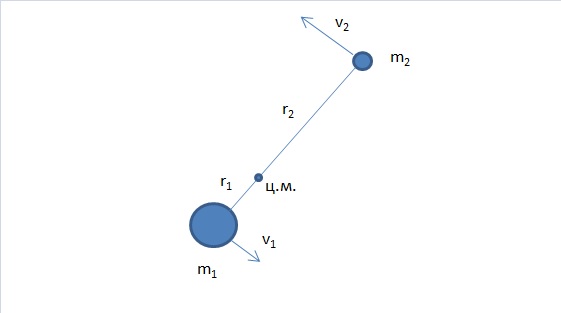
Уравнения движения для нашей системы можно получить с помощью уравнений Лагранжа второго рода. Для этого нам потребуется найти кинетическую Т и потенциальную энергию U для системы материальных точек m1, m2 (Рис. 1), связанных гравитационным взаимодействием.
Пусть r=r1+r2 . Из определения центра масс (ц.м.) следует, что :
Радиальные скорости равны соответственно:
Запишем моменты инерции тел относительно центра масс:
Момент инерции всей системы равен сумме моментов инерции входящих в нее тел:
Перед квадратом радиуса стоит половина среднего гармонического наших масс. Обозначим ее µ.
Кинетическая энергия первого тела складывается из двух компонент – поступательной и вращательной:
То же можно сказать и о втором теле:
Полная кинетическая энергия системы двух тел равна:
Потенциальная энергия системы равна:
Запишем лагранжиан для нашей системы:
Зависимость от времени координаты r получим из уравнения Лагранжа:
Дифференцируя действие, получим:
Сокращая на µ равенство (11), получим уравнение для расстояния между центрами тел:
Закон сохранения момента импульса позволяет нам сделать подстановку:
где I=µr2- момент инерции пары тел.
И в итоге уравнение (12) примет вид:
Для сравнения стоит взглянуть на аналогичное уравнение движения тела пренебрежимо малой массы:
Здесь L0 это момент импульса тела пренебрежимо малой массы при его движении вокруг массивного тела, который равен:
где Vотн- скорость второго (малого) тела относительно центра первого.
Момент импульса нашей системы равен:
Выразим его через параметры второго тела, используя соотношения:
и с учетом (1) для начального момента времени, когда оба тела проходят перицентр своих траекторий, получим:
Обратим внимание, что оба тела движутся относительно центра масс, и скорость второго тела относительно первого равна:
или, вводя коэффициент alpha=(m1+m2)/m1, который всегда больше единицы:
Откуда следует, что , L=L0/alpha т.е. суммарный момент импульса тел сравнимой массы, вращающихся около центра масс, меньше, чем момент импульса тела пренебрежимо малой массы, вращающегося около массивного тела при условии, что в перицентре начальные скорости меньшего тела относительно центра большего были равны.
Нетрудно показать, что
Это соотношение есть не что иное, как постоянная площадей:
Это означает, что движение тела значительной массы относительно центра большего тела происходит точно по той же орбите, по которой двигалось бы тело пренебрежимо малой массы в поле тела с массой, равной сумме масс пары тел.
Мы доказали, что суммарный момент импульса тел в случае, когда массой меньшего тела нельзя пренебрегать, меньше момента импульса тела пренебрежимо малой массы, не смотря на равенство их относительных скоростей в перицентре. То же можно сказать и о полной энергии системы, а, следовательно, и о большой полуоси эллиптической орбиты, и о периоде обращения (Рис. 2 и Рис. 3). Все значения параметров на этих рисунках нормированы к таковым при условии, что масса второго тела пренебрежимо мала.
Обозначим теперь массу большего тела M, а массу меньшего тела m. Фокальный параметр в таком случае равен:
Эксцентриситет:
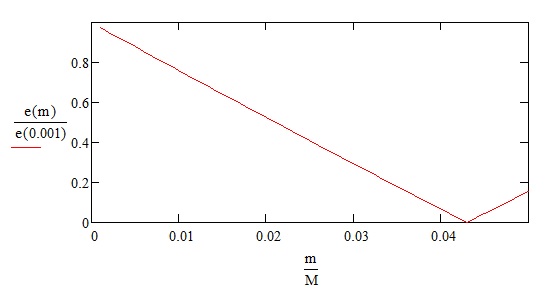
Рис. 2.
Большая полуось орбиты равна:
Период обращения:
Этой формулой можно попробовать воспользоваться для оценки суммы масс Земли и Луны, а следовательно, отношения массы Луны к массе Земли, поскольку масса Земли хорошо известна. Она равна 5,9726 1024 кг.
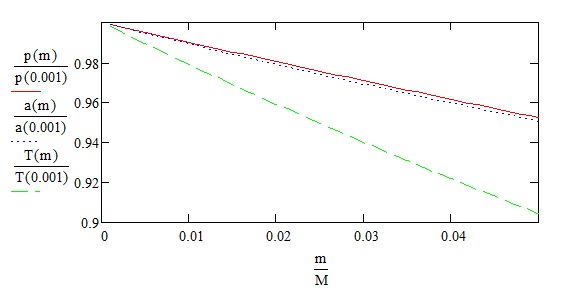
Рис. 3.
Если в качестве большой полуоси орбиты мы возьмем среднее расстояние между центрами Земли и Луны за большой промежуток времени, а в качестве периода обращения аномалистический период, то получим некоторую оценку суммы масс Земли и Луны.
Любой исследователь может взять эфемериды Луны с сайта http://ssd.jpl.nasa.gov/horizons.cgi. Мне стали доступны временные ряды расстояния Земля-Луна за 20 лет с 2000 по 2019 год. Арифметическое среднее для расстояния оказалось равным 385050 км, а аномалистический период (промежуток времени между перигеями или апогеями) 27,55 средних солнечных суток. При подстановке этих значений в следующую формулу:
получается, что сумма масс Земли и Луны меньше массы Земли. Абсурд.
Может быть, стоит взять в расчет не аномалистический период, а сидерический, который равен 27,32 сут? Тогда отношение массы Земли к массе Луны составит 64,98. Опять не то.
Может быть, среднее расстояние между Землей и Луной нужно считать иначе? Среднее геоцентрическое расстояние между Землей и Луной по радиолокационным измерениям3 равно 384400,2±1.1 км. В этом случае получается, что Земля тяжелее Луны в 97.49 раз.
Многое о движении Луны может рассказать скорость прохождения ею перигея. Воспользуемся все теми же эфемеридами с сайта JPL.
|
Дата |
Прямое восхождение, часы |
Склонение, ° |
Расстояние, км |
|
18.06.2002 |
11,91 |
6,3 |
369856 |
|
19.06.2002 |
12,77 |
0,3 |
369399 Перигей |
|
20.06.2002 |
13,64 |
-5,7 |
369513 |
В очень грубом приближении из данных таблицы мы можем оценить среднюю угловую скорость Луны при прохождении ею участка орбиты, содержащего точку перигея, и найти тангенциальную скорость в перигее:
.JPG)
Подставляя числовые значения, получим Vp=964м/с.
Имея такую скорость на расстоянии 369400 км от центра Земли, в приближении задачи двух тел Луна обращалась бы с периодом в 21 сутки и имела перигей на высоте 273500 км. Однако Солнце помогает ей летать гораздо выше. Но это уже другая история, а именно ЗАДАЧА ТРЕХ ТЕЛ.
Источники информации
1. В. И. Арнольд, В. В. Козлов, А. И. Нейштадт, “Математические аспекты классической и небесной механики”, Динамические системы – 3, Итоги науки и техн. Сер. Соврем. пробл. мат. Фундам. направления,3, ВИНИТИ, М., 1985, 5–290
2. Крылов, Алексей Николаевич. Собрание трудов академика А.Н. Крылова. Т. 7. Ис. Ньютон. Математические начала натуральной философии / Пер. с лат. с прим. и поясн. А.Н. Крылова. - М. ; Л. : Изд-во АН СССР, 1936. - 696 с.
3. Справочное руководство по небесной механике и астродинамике / В.К. Абалакин, Е.П. Аксенов, Е.А. Гребеников, В.Г. Демин, Ю.А. Рябов ; под ред. Г.Н. Дубошина. М.: Наука, 1976. 864 с.
- Ingus's блог
- Войдите на сайт для отправки комментариев
- 5124 просмотра


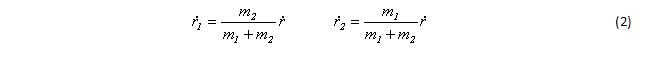
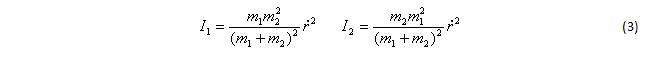
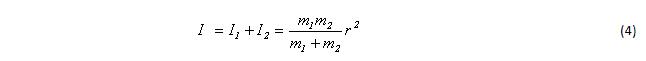
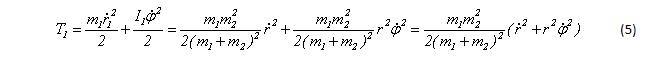
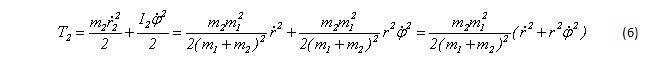


.JPG)
.JPG)
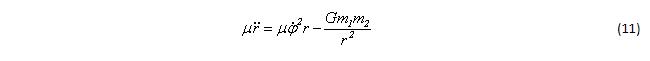
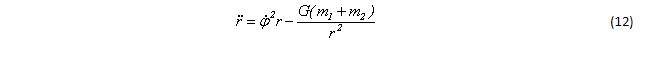
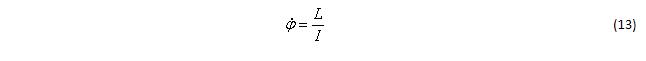
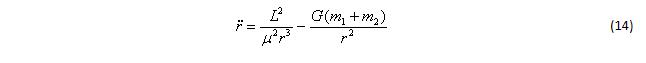
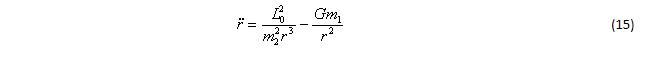
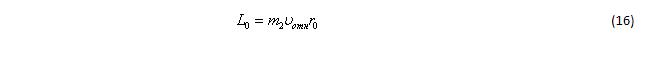
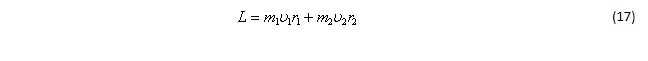
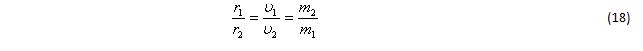
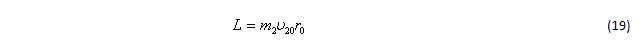
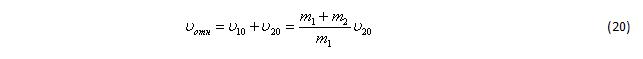
.JPG)
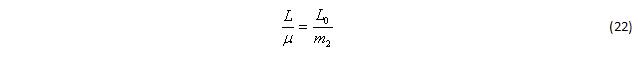
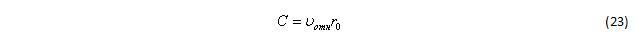
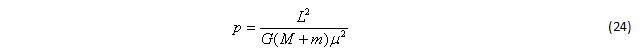
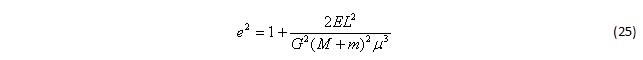
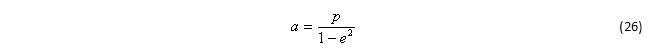
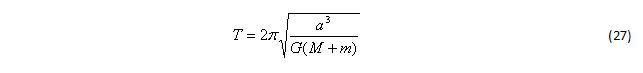
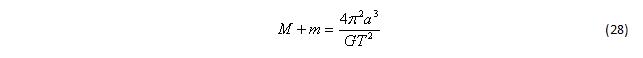


За поддержку Космофизического практикума спасибо, материал обязательно внимательно посмотрим.
Кстати, для космофизического практикума можно использовать данные JPL NASA. В том числе орбитальные характеристики Луны, планет и спутников. Пока они доступны)