Насколько проверена ОТО?
Цитата из письма:
"Но ньютоновская механика не могла объяснить
аномалию смещения перигелия Меркурия, тогда как ОТО точно предсказала величину смещения, что стало ключевым тестом для признания ОТО."
На сегодняшний момент существует три базовых эксперимента, которые, как считается, подтверждают ОТО (Общая теория относительности). Это
измерение смещения перигелия Меркурия,
отклонение света звезд вблизи Солнца и
красное смещение частоты лазерного излучения в поле тяготения Земли (эксперимент Паунда-Ребки).
Сейчас добавляют к этому еще существование гравитационных волн, линзирование и даже черные дыры. По поводу этих последних трех разговор особый, поскольку такие эффекты будут появляться в любой теории, где допускаются изменения метрики пространства за счет тяготения, а черные дыры - это вещь в себе. Они есть и в классической физике, но без понимания их внутреннего устройства. Поэтому скажу несколько слов только о первом эксперименте и немного о втором. Про остальные будет отдельная статья на сайте.
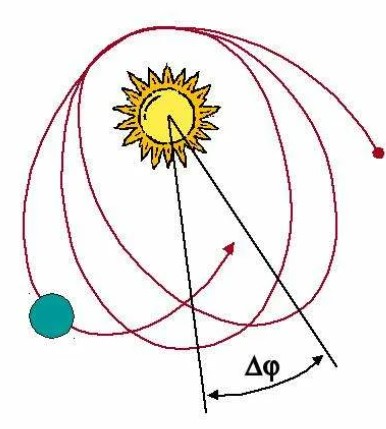
Измерение смещения перигелия Меркурия дает очень хорошее согласие с оценкой ОТО. Сама оценка строится на поправке к потенциалу тяготения Солнца вида $\sim r^{-3}$. Эта поправка следует из, вроде бы очевидных, предположений, что гравитационное поле Солнца сферическое, а масса сосредоточена внутри сферы измеренного ранее радиуса Солнца $R\simeq 700\ 000$ км.
На самом деле эти предположения, особенно в последние пару десятилетий, несколько подвергаются сомнению. Первая проблема со сферичностью Солнца. Солнце вращается с периодом на экваторе около 26 дней. Линейная скорость на экваторе около 2 км/c. Поэтому Солнце обязательно слегка сплюснуто на полюсах. К чему это приводит?
При такой сплюснутости в потенциале тяготения появляется та же самая поправка $\sim r^{-3}$. Например, у Земли экваториальный радиус примерно на 21 км больше полярного. Это приводит к тому, что перигелии спутников на высотах порядка 1000 км делают полный оборот вокруг Земли за три-четыре (бывает и больше) месяца в зависимости от наклонения орбиты и ее высоты.
 |
| Вращение орбиты спутника за счет сплюснутости Земли |
Этот эффект должен наблюдаться и у ближайших спутников Солнца. Чем дальше от притягивающего тела, тем эффект меньше. Для оценки этого эффекта у Солнца надо измерить его сплюснутость. Но вот это пока не удается. Лет так двадцать назад на одной из астрофизических конференций этот вопрос кто-то поднял в докладе. Но к чему-то существенному тогда не пришли. В последнее время никаких публикаций по этому поводу я не видел. Однако сам факт обязательного наличия этого эффекта ставит под вопрос совпадение оценки ОТО смещения перигелия Меркурия с результатами измерения.
Второй эффект, который стал важным в последнее десятилетие и который может также существенно исказить реальные оценки смещения перигелия Меркурия и отклонения света звезд - это распределение массы вещества вблизи Солнца. В стандартной модели Солнца до сих пор не учитывается то, что масса Солнца распределена совсем не так строго внутри радмуса $R\simeq 700\ 000$ км. В общем об этом можно было бы догадаться и раньше.
Но сравнительно недавно астрофизики обнаружили, что после фотосферы Солнца, где температура падает до $\simeq 4800 K$, температура вновь начинает расти до примерно $2\ 000\ 000 K$, при том, что по стандартной модели температура в центре Солнца $\simeq 15\ 000\ 000 K$. Проблема часто позиционируется как "проблема нагрева короны". Этот максимум располагается, как считают, примерно на 1/10 радиуса Солнца. Стандартная модель Солнца не объясняет этот максимум. Этот максимум существует всегда, т. е. должен входить в задачу о равновесии Солнца и ее короны. Это означает, что существенная часть солнечной массы располагается не внутри сферы, границей которой является фотосфера, а гораздо дальше.
"На пальцах" это выглядит так. В равновесии плотность и температура связаны адиабатическим соотношением $T=K_0 \rho^{\gamma}$, где $\gamma$ - показатель адиабаты, а $K_0$ - некоторая постоянная. Для Солнца в стандартной модели полагают $\gamma = 5/3$ (одноатомный газ). Это не совсем верно, но для грубых оценок годится. Из адиабатического соотношения следует, что при падении температуры с $15\ 000\ 000 K$ до $2\ 000\ 000 K$ плотность падает в $(7.5)^{3/5}$, т.е. всего в 3.4 раза. Однако объем, в котором распределена масса, увеличивается как $r^3$. Т.е. при увеличении радиуса в два раза, объем вырастает в 8 раз. Поэтому масса внутри объема удвоенного радиуса уже будет сравнима с массой Солнца. Дальше плотность падает, стремясь к некоторой ненулевой постоянной в равновесии. Но кубический рост объема ведет к тому, что существенная часть массы Солнца сосредоточена в короне. А оценки ОТО этого не учитывают.
Сравнительно медленное падение массы за пределами фотосферы вытекает из новой модели 2022 года, которую опубликовал в ЖЭТФ, а потом в других журналах еще пару статей. Модель называется моделью динамического равновесия звезд, в которой максимум в короне является обязательным атрибутом и требует какого-то специфического нагрева. В этом подходе как раз использовался новый вариант описания классического поля тяготения, которое восходит к идеям новой теории. Модель еще не полностью доработана, но явно противоречит стандартной модели, основанной на статическом равновесии. Но это отдельный вопрос.
.jpg) |
|
Качественное распределение температуры вблизи Солнца, |
Из простых оценок, которые приведены выше, и которые практически модельно не зависимы, следует, что потенциал тяготения Солнца падает не так, как если бы вся масса была бы сосредоточена внутри фотосферы. Это дает дополнительный вклад в смещение перигелия Меркурия и, естественно, в оценку отклонения света звезд вблизи Солнца.

Поэтому то, что в ОТО эти оценки при неучете указанных эффектов совпадают с измерениями очень хорошо, является скорее проблемой, а не реальным подтверждением. Так что с ОТО в этом плане тоже не все гладко.
- Войдите на сайт для отправки комментариев
- 350 просмотров


