Проект № 16-42-732113 и 16-42-732119 офим-м РФФИ (2)
2. Многозначные решения уравнений гиперболического и эллиптического типов
2.1. Классификация автономных квазилинейных уравнений первого порядка
2.1.1. Простейшая модель
Одной из самых простых моделей нелинейной гидродинамической волны является модель, описывающаяся уравнением первого порядка вида:$$u_t+uu_x=0,\tag{2.1}\label{EqSplW}$$
Это уравнение часто так и называется: "уравнение простой волны". Его не существенное обобщение: $$u_t+V(u)u_x=0,\tag{2.2}\label{EqHopfS}$$ где $V(u)$ - произвольная дифференцируемая функция неизвестной функции $u(x,t)$ называют часто уравнением Хопфа. Уравнение (\ref{EqHopfS}) превращается в уравнение (\ref{EqSplW}) с помощью умножения его на функцию $V'(u)$ и замены переменной $V(u)\to u(x,t)$. Основной особенностью уравнений (\ref{EqSplW}) и (\ref{EqHopfS}) является то, что они описывают явление, называемое опрокидыванием волны [1,2]\cite{RYa78,KSCh11}. Смысл этого явления иллюстрируют графики на рисунке (1), которые построены с помощью известного точного решения уравнения (\ref{EqSplW}):
$$u=H(x-u t),\tag{2.3} \label{SolSW}$$
где $H(\xi)$ - произвольная дифференцируемая функция аргумента $\xi=x-u(x,t)t$.
На рис. (1) представлено решение уравнения простой волны, соответствующее, начальному распределению функции $u(x,t)$ следующего вида:
$$u(x,0)={\rm ch}^{-1}(x).$$
$$u(x,0)={\rm ch}^{-1}(x).$$
.jpg)
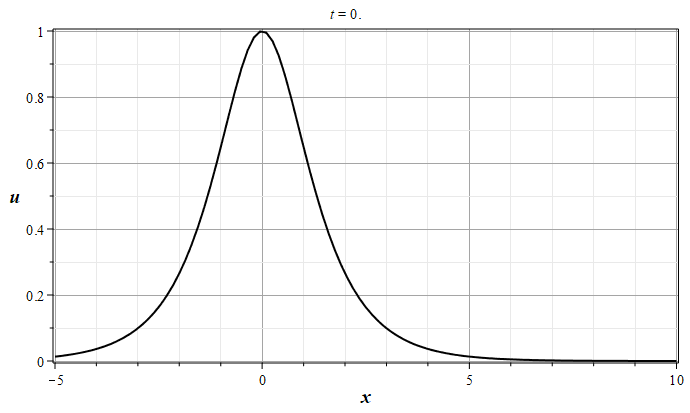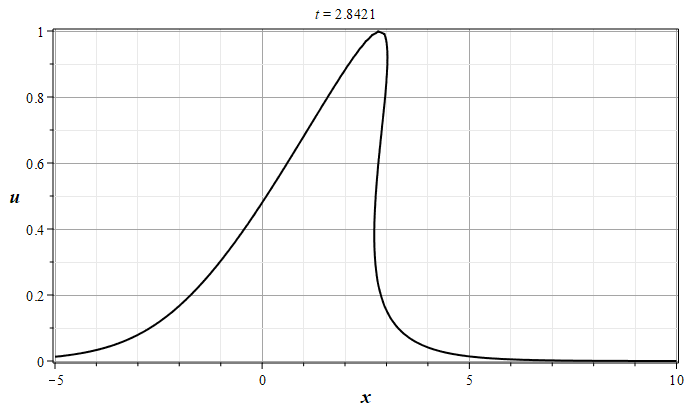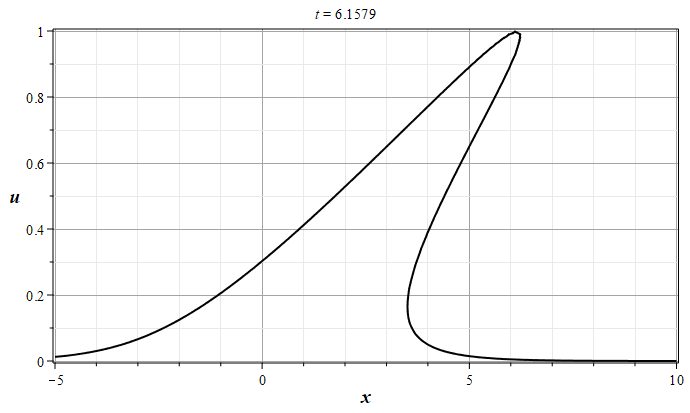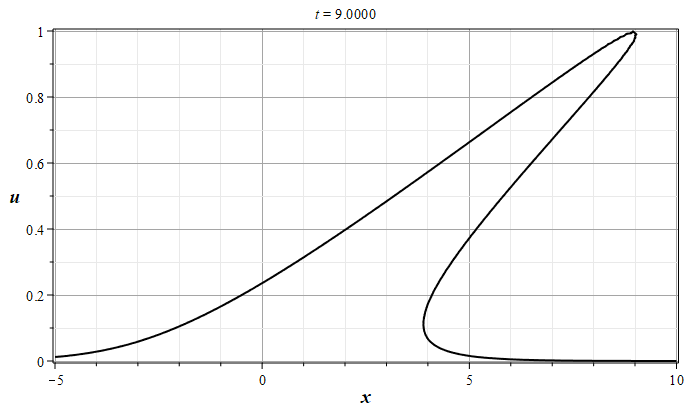
Рис. 1. Эволюция решения уравнения простой волны (\ref{EqSplW}), 0 - $t=0$, 8 - $t=4.0$ (с шагом $\Delta t = 0.5$)
Из графиков видно, что первоначально уединенная волна, имеющая один максимум функции $u(x,0)$ и не имеющая особенностей, со временем приходит в состояние, когда в оной из точек пространства ($x_0$) производная функции $u(x,t)$ по координате обращается в бесконечность. На графике это состояние обозначено цифрой 2. Дальнейшая эволюция волны приводит к образованию области многозначности функции $u(x,t)$, в которой функция $u(x,t)$ может иметь три несовпадающих между собой вещественных значения. С физической точки зрения такая ситуация не возможна, если только не привлекать каких либо соображений о разделении потока частиц на три составляющих, чего в начальной постановке задачи не было. Поэтому в физических приложения при интерпретации непрерывных почти всюду многозначных решений их заменяют на разрывные однозначные решения с помощью дополнительных соотношений на функции среды. В такой интерпретации опрокидывающиеся волны называют ударными волнами. Ударные волны являются реально наблюдаемыми явлениями, которые возникают, например, в области взрывов [1,2] \cite{RYa78,KSCh11}.
Поэтому такие задачи оказываются очень важными в тех ситуациях, когда важно описать общий характер эволюции процессов взрыва, отбрасывая процессы вязкости и диффузии, которые играют существенную роль лишь вблизи границ области многозначности. Это определяет важность задач такого рода для гидродинамики процессов в различных областях прикладных разделов типа теории горения до теории эволюции звезд.
Уравнения типа (\ref{EqHopfS}) в различных обобщенных вариантах будет встречаться далее достаточно часто. Общим для всех таких уравнений будет то, что их решение строятся с помощью метода характеристик и будут иметь общий вид:$$u(x,t)=H(\xi(x,t)),\tag{2.4}\label{SolHopf}$$где $H(\xi)$ - произвольная дифференцируемая функция аргумента $\xi$, который выражается через неизвестную функцию $u(x,t)$ и переменные $x$ и $t$: $\xi=X(u,x,t)$. Именно такие уравнения мы будем назвать уравнениями Хопфа. В частности, уравнение (\ref{EqHopfS}) имеет следующее решение:$$u(x,t)=H\Big(x-V(u)t\Big),\tag{2.5}\label{SolHopfS}.$$
2.1.2. Классификация в многомерном случае
I. Первый тип
Уравнения простой волны и Хопфа в многомерном пространстве имеют несколько обобщений. Наиболее простое обобщение состоит в переходе к уравнению переноса гидродинамическим потоком в пространстве $d$ измерений с координатами ${\bf x}=(x^1,x^2,\dots,x^d)$ некоторой субстанции, характеризующейся параметром $E({\bf x},t)$, со скоростью ${\bf u}=(u^1(E),u^2(E),\ldots,u^{d}(E))$, зависящей только от этого параметра. Соответствующее квазилинейное уравнение имеет такой вид:$$E_t+\sum\limits_{i=1}^du^{i}(E)E_{,i}=0,~~E_{,i}=\frac{\partial}{\partial x^i}.\tag{2.6}\label{EqEd}$$ Это уравнение имеет следующий общий интеграл движения:
$$H\Big(E,x^1-u^1(E)t,x^2-u^2(E)t,\ldots,x^d-u^d(E)t\Big)=0,\tag{2.7}\label{SolEqEd}$$
сводящий задачу построения решения к алгебраической задаче вычисления корней уравнения (\ref{SolEqEd}) относительно $u$ при произвольном выборе самой функции $H(u,\xi^1,\ldots,\xi^d)$. Этот интеграл движения можно построить, используя метод характеристик, но можно проверить и прямыми вычислениями с помощью дифференцирования по $t$ и $x^i$ (\ref{SolEqEd}). Действительно:$$\frac{\partial H}{\partial t}=H_{,E}E_t-\sum\limits_{i=1}^d H_{,\xi^i}\Big(u^i(E)+t(u^i)'E_t\Big)=0,$$$$\frac{\partial H}{\partial x^j}=H_{,E}E_{,i}+\sum\limits_{i=1}^d H_{,\xi^i}\Big(\delta^{i}_j-t(u^i)'E_{,j}\Big)=0$$
Вычисляя из первого уравнения этой системы $H_{,E}$ и подставляя в последующие, приходим к следующей системе линейных алгебраических уравнений относительно производных $H_{,\xi^i}$:$$\sum\limits_{i=1}^d H_{,\xi^i}\left(E_t\delta^{i}_j+u^i(E) E_{,j}\right)=0,~~j=1,\ldots,d.$$ Эта система однородна, поэтому условием существования нетривиальных решений является условие равества ее детерминанта нулю, что эквивалентно (\ref{EqEd}). Что и требовалось доказать.
II. Второй тип
Другим примером системы уравнений, описывающей опрокидывание волны в многомерном пространстве, является система квазилинейых уравнений следующего вида:
$$E_{,i}=A_{i}(E)E_t,~~i=1,\ldots,d.\tag{2.8}\label{EqQLn}$$ Эта система имеем интеграл движения вида:$$H\left(E,t+\sum\limits_{i=1}^dA_{i}(E)x^i\right))=0.\tag{2.9}\label{SolHd}$$
Дифференцируя (\ref{EqQLn}) по $t$ и координатам $x^{j}$, приходим к системе алгебраических уравнений:$$E_{,j}H_{,E} + \Big(A_{j}+({\bf A}'(E),{\bf x})E_{,j}\Big)H_{\eta}=0,~~~j=1,\ldots,d;$$$$E_{,t}H_{,E} +\Big(1+({\bf A}'(E),{\bf x})E_{t}\Big)H_{\eta}=0.\tag{2.10}\label{EqDiffH}$$ Здесь $\eta=t+\sum\limits_{i=1}^dA_{i}(E)x^i$. Исключая из этой системы уравнений производные функции $H(\xi,\eta)$, получаем систему уравнений (\ref{EqQLn}).
III. Системы типа $QL^{mn}$
Для описания общего класса квазилинейных уравнений, которые будут рассмотрены в дальнейшем, введем в рассмотрение координатное пространство, состоящее из двух под пространств, размерности $n$ и $m$ соответственно. Координаты в первом подпространстве будем обозначать ${\bf x}=(x^1,\ldots,x^n)$, а во втором - ${\bf y}=(y^1,\ldots,y^m)$. Тогда уравнения рассматриваемого типа относительно функции $E({\bf x},{\bf y})$ можно представить в следующим виде:$$\frac{\partial E}{\partial x^{\alpha}}=\sum\limits_{a=1}^mA_{\alpha}^a(E)\frac{\partial E}{\partial y^a},~~\alpha=1,\ldots,n.\tag{2.11}\label{EqQLnm}$$
Система квазилинейных уравнений (\ref{EqQLnm}) имеет общий интеграл следующего вида:$$H\Big(E,y^1+\Phi^1(E,{\bf x}),\ldots,y^m+\Phi^{m}(E,{\bf x})\Big)=0,\tag{2.12}\label{SolHnm}$$ где $$\Phi^{a}(E,{\bf x})=\sum\limits_{\alpha=1}^nA^{a}_{\alpha}(E)x^{\alpha},~a=1,\ldots,m.\tag{2.13}\label{DefPhiL}$$
Доказательство строится по аналогии с доказательством (\ref{SolHnm}). Дифференцируя (\ref{SolHnm}) по координатам $x^\alpha$ и $y^{a}$, получаем следующую систему уравнений: $$\frac{\partial H}{\partial x^{\alpha}}=H_{,E}E_{,\alpha}+\sum\limits_{b=1}^M \Big(E_{,\alpha}\Phi^b_{,E}+A^b_{\alpha}\Big)H_{,b}=0,\tag{2.14}\label{EqDifI}$$$$\frac{\partial H}{\partial y^{a}}=H_{,E}E_{,a}+\sum\limits_{b=1}^M \Big(\delta_{b}^a+E_{,a}\Phi^b_{,E}\Big)H_{,b}=0.\tag{2.15}\label{EqDifII}$$ Вторая часть (\ref{EqDifII}) данной системы представляет систему aлгебраических уравнений относительно производных: $$H_{,b}=\frac{\partial H}{\partial\xi^b},~~H_{,E}=\frac{\partial H}{\partial E},~~\xi^b=y^b+\Phi^b(E,{\bf x})$$ с матрицей ${\bf M}$, имеющей элементы: $$M_{b}^a=\delta_{b}^a+E_{,a}\Phi^b_{,E}.$$ Эта матрица имеет определитель: $$D_M=\det{\bf M}=1+\sum\limits_{b=1}^mE_{,b}\Phi^b_{,E},\tag{2.16}\label{DefDM}$$ а элементы обратной матрицы ${\bf M}^{-1}$ можно представить в следующем виде: $$\Big(M^{-1}\Big)_{b}^a=\delta_{b}^a-\frac{1}{D_M}E_{,a}\Phi^b_{,E},~~a,b=1,\ldots,m$$
Отсюда, используя (\ref{DefDM}), находим решение системы (\ref{EqDifII}): $$H_{,b}=-H_{,E}\sum\limits_{a=1}^m\Big(\delta_{b}^a-D_M^{-1}E_{,b}\Phi^a_{,E}\Big)E_{,a}=-H_{,E}\frac{1}{D_M}E_{,b},~~b=1,\ldots,m.\tag{2.17}\label{SolMII}$$ Подставляя это решение в первую часть (\ref{EqDifI}), приходим к следующему выражению: $$\frac{1}{D_M}H_{,E}\Big(D_M E_{,\alpha}-\sum\limits_{b=1}^M \Big(E_{,\alpha}\Phi^b_{,E}+A^b_{\alpha}\Big)E_{,b}\Big)=0,~~b=1,\ldots,m$$ Это уравнение будет обращаться в ноль при любых значениях $H_{,E}$ тогда и только тогда, когда выполнено условие: $$D_ME_{,\alpha}-\sum\limits_{b=1}^M \Big(E_{,\alpha}\Phi^b_{,E}+A^b_{\alpha}\Big)E_{,b}=0,~~\alpha=1,\ldots,n$$ которое, после раскрытия скобок и подстановки $D_M$ из (\ref{DefDM}), превращается в уравнение (\ref{EqQLnm}), что и доказывает (\ref{SolHnm}).
Определение. В дальнейшем систему многомерных квазилинейных уравнений первого порядка (\ref{EqQLnm}) будем обозначать через $QL^{(n,m)}$. В частности, системы (\ref{EqEd}) и (\ref{EqQLn}) имеют обозначения $QL^{(n,1)}$ и $QL^{(1,n)}$, соответственно.
2.2. Свойства решений многомерных квазилинейных уравнений $QL^{n,m}$
2.2.1. Решения системы $QL^{n,1}$. Ривертоны
Решения уравнения системы квазилинейных уравнений (\ref{EqQLn}) обладают особыми свойствами, которые отличают их от решений одномерных квазинейных уравнения (излагаетсмя по тексту статьи Журалвев В.М., ТМФ, 2013). Одномерные квазилинейные уравнения описывают опрокидывние волны при перемещении ее вдоль характеристик. Опрокидывание возникает в точках, где характеристики пересекаются. Уравнения же $QL^{n,1}$ демонстрируют другой тип многозначности, связанный с пересечением фронтов волны, хотя пересечение характеристик также может иметь место.
Сама геометрическая структура системы уравнений (\ref{EqQLn}) определяет характер ее решений. Векторное поле ${\bf A}={\bf A}(E({\bf x},t))$ в заданный момент времени $t$ зависит только от значения функции $E$. Поэтому это векторное поле постоянно на изоповерхностях функции $E$: $\left.{\bf A}\right|_{E=const}=const$. Однако согласно самим уравнениям (\ref{EqQLn}) поле ${\bf A}$ коллинеарно в каждой точке пространства полю $\nabla E$, которое для каждого момента времени $t$ всюду ортогонально гиперповерхности $E({\bf x},t)=E_{0}(t)=const$. Отсюда следует, что в каждый фиксированный момент времени $t$ изоповерхностями функции $E$ являются гиперплоскости, поскольку в любой точке этой гиперповерхности нормаль к ней имеет одно и тоже направление, зависящее только от $E(t)$. Это означает, что с геометрической точки зрения решение уравнений(\ref{EqQLn})} можно описать как однопарметрическую последовательность гиперплоскостей, на каждой из которых решение имеет постоянное значение, но возможно зависящее от времени. Поэтому для вычисления зависимости значений решений на гиперплоскостях достаточно рассматривать решение вдоль одной кривой, всюду перпендикулярной к гиперплоскостям решения. В результате справедливо следующее утверждение.
Утверждение 4. Решение системы (\ref{EqQLn}) $E({\bf x},t)$ призаданной функции $R(E)=|{\bf A}(E)|$ определяется однозначно парой функциональных параметров $\{{\cal C}_n,E(s,t)\}$, в которой ${\cal C}_n$ является независящей от времени однопараметрической кривой, называемой далее базовой: $$ \frac{dx^\alpha}{ds} = n^{\alpha}(s),~~~n^{\alpha}(s)=A^{\alpha}(E(s))/R(s),\tag{2.17}\label{EqCurn}$$ в координатном пространстве ${\cal R}^n$, и функцией $E(s,t)=E({\bf x}(s),t)$ - являющейся решением уравнения Хопфа: $$\frac{\partial E}{\partial s} = R(E)\frac{\partial E}{\partial t}.\tag{2.18}\label{EqHopf}$$
Доказательство. Поскольку выше было доказано, что изоповерхностями функции $E({\bf x},t)$ являются гиперплоскости, к которым ортогональны поля $({\bf A}=R{\bf n}(E)$, где ${\bf n}(E)$ - единичный вектор вдоль направления ${\bf A}(E)$, то существует кривая ${\cal C}_n$, касательная к которой в каждой точке кривой ортогональна одной из гиперплоскостей, проходящей через эту точку. По определению такая кривая может быть описана уравнением (\ref{EqCurn}).
Пусть ${\cal C}$ - кривая, заданная уравнением (\ref{EqCurn}). Тогда, используя систему уравнений (\ref{EqQLn}), имеем: $$\frac{\partial E}{\partial s} = \sum\limits_{\alpha=1}^n\frac{\partial E}{\partial x^\alpha}\frac{\partial x^{\alpha}}{\partial s}= \sum\limits_{\alpha=1}^n R(E)E_t n^{\alpha}(E(s,t))n^{\alpha}(E(s,t))=R(E)E_t.\tag{2.19}\label{EqHopf1}$$
Последнее равенство следует из условия $|{\bf n}|^2=\sum\limits_{\alpha=1}^n n^{\alpha}n^{\alpha}=1$. Отсюда сразу следует (\ref{EqHopf1}). Заметим, что решение $E(s,t)$ уравнения Хопфа находится как решение уравнения: $$H(E,t+R(E)s)=0,\tag{2.20}\label{SolHopf2}$$ где $H(\xi,\eta)$ та же функция, что и в решении (\ref{SolHd}), что соответствует выбору параметра $s$ по формуле:$$\sum\limits_{\alpha=1}^n n^{\alpha}(E(s,t))x^{\alpha}(s)=s.$$ В результате решение (\ref{SolHd}) переходит в решение (\ref{SolHopf2}).
Пусть задана некоторая базовая кривая ${\cal C}_n$ ривертона в форме системы уравнений (\ref{EqCurn}). Интегрируя эту систему приходим к параметрическому заданию данной кривой в форме уравнений: $$x^{\alpha}=X^{\alpha}(s) = \int n^{\alpha}(s)ds + x^{\alpha}_0.$$ Постоянные $x^{\alpha}_0$ указывают положение кривой относительно начала координат. В этом случае гиперплоскости уровня $E={\rm const}$ в ${\cal R}^n$, соответствующие заданному значению параметра $s$, можно записать в виде уравнения: $$\sum\limits_{\alpha=1}^n x^{\alpha}n^{\alpha}(s)= \sum\limits_{\alpha=1}^n X^{\alpha}(s)n^{\alpha}(s)=\frac{1}{2}\frac{d}{ds}\sum\limits_{\alpha=1}^n \Big[X^{\alpha}(s)\Big]^2.$$
Две гиперплоскости, отвечающие двум значениям $s_1$ и $s_2$ параметра $s$ пересекаются в пространстве ${\cal R}^n$ по совокупности точек, являющихся решением двух таких уравнений: $$\sum\limits_{\alpha=1}^n x^{\alpha}n^{\alpha}(s_1)= F(s_1),~~~~\sum\limits_{\alpha=1}^n x^{\alpha}n^{\alpha}(s_2)= F(s_2),$$ где $$F(s)=\frac{1}{2}\frac{d}{ds}\sum\limits_{\alpha=1}^n \Big[X^{\alpha}(s)\Big]^2. \tag{2.21}\label{EqP12}$$ Эти совокупности точек образуют в ${\cal R}^n$ гиперплоскости размерности $n-2$. Огибающая множества всех таких гиперплоскостей будет образовывать границу областей однозначности и многозначности ривертона.
Огибающую области многозначности без ограничения общности можно вычислить следующим образом. Огибающая состоит из точек пересечения всех бесконечно близких гиперплоскостей при $s_1\to s_2$. Систему (\ref{EqP12}) можно разрешить относительно первых двух координат $x_1$ и $x_2$, в результате чего они становятся функциями $s_1$ и $s_2$, а так же остальных координат $x_{3},\ldots,x_{n}$: $$x_1(s_1,s_2) = \frac{G(s_2,{\bf x})n^2(s_1)-G(s_1,{\bf x})n^2(s_2)}{n^2(s_1)n^1(s_2)-n^2(s_2)n^1(s_1)},\tag{2.22}\label{EqExE}$$$$x_2(s_1,s_2) = -\frac{G(s_2,{\bf x})n^1(s_1)-G(s_1,{\bf x})n^1(s_2)}{n^2(s_1)n^1(s_2)-n^2(s_2)n^1(s_1)}.$$ Здесь $$G(s,{\bf x})=F(s)-\sum\limits_{\alpha=3}^n x^{\alpha}n^{\alpha}(s).$$ В пределе $s_1\to s_2\to s$ мы получаем уравнение гиперплоскости ${\cal E}^{n-2}(s_1,s_2)$ размерности $n-2$, являющейся пересечением двух бесконечно близких гиперплоскостей $E=E(s_1)$ и $E=E(s_2)$. В пределе $s_1\to s_2\to s_0$ получаем множество $\{{\cal E}^{n-2}(s_0)\}$ гирперплоскостей, зависящих от параметра $s_0$, образующих гиперповерхность ${\cal G}^{n-1}$, к которой касательны все гиперплоскости $E=E(s_0)$ для значений параметра $s_0$ в некотором интервале $(s_1,s_2)$. Поскольку все гиперплоскости $E=E(s)$ из интервала $s\in (s_1,s_2)$ касательны к ${\cal G}^{n-1}$, то они пересекаются друг с другом в области, лежащей в ${\cal R}^n$ с одной стороны по отношению к ${\cal G}^{n-1}$. Следовательно, гиперповерхность ${\cal G}^{n-1}$ разделяет области многозначности и однозначности ривертона, по крайней мере, для интервала $(s_1,s_2)$ параметра $s$. Переходя к пределу $s_1\to s_2\to s$ в соотношениях (\ref{EqExE}), получаем уравнения параметрического задания гиперповерхностей ${\cal G}^{n-1}$: $$x_1(s) = \frac{G'_1(s,{\bf x})}{N'_1(s)},~~x_2(s)=\frac{G'_2(s,{\bf x})}{N'_2(s)},\tag{2.23}\label{EqX1}$$ где $$G'_1(s,,{\bf x}) = \frac{d}{ds}\left(\frac{G(s,{\bf x})}{n^1(s)}\right),~~G'_2(s,{\bf x}) = \frac{d}{ds}\left(\frac{G(s,{\bf x})}{n^2(s)}\right),$$$$N'_1(s) = \frac{d}{ds}\left(\frac{n^1(s)}{n^2(s)}\right),~~N'_2(s) = \frac{d}{ds}\left(\frac{n^2(s)}{n^1(s)}\right).$$
На рис. (1)-(4) приведены примеры вычисления областей однозначности и многозначности ривертонов для размерности координатного пространства $n=2$ в случае базовых кривых:$$(1):~~ X(s) = s,~~ Y(s) = \cos(s);$$$$ (2):~~ X(s) = s+\sin(s),~~ Y(s) = \cos(s),$$$$(3):~~X(s)=s=Y(s)=1/(1+s^2).$$$$(4):~~ X(s)=s,~~Y(s)={\rm th}(s),$$ Базовые кривые выделены жирной сплошной кривой. На рисунках сплошными прямыми обозначены линии уровня $E=const$ (фронты ривертона). Фронты ортогональны базовой кривой. Области их многократного пересения и есть области многозначности решений. На эту картину фронтов накладывается динамика самой волны, которая может опрокидваться со временем вдоль прямых $E={\rm const}$.
Две гиперплоскости, отвечающие двум значениям $s_1$ и $s_2$ параметра $s$ пересекаются в пространстве ${\cal R}^n$ по совокупности точек, являющихся решением двух таких уравнений: $$\sum\limits_{\alpha=1}^n x^{\alpha}n^{\alpha}(s_1)= F(s_1),~~~~\sum\limits_{\alpha=1}^n x^{\alpha}n^{\alpha}(s_2)= F(s_2),$$ где $$F(s)=\frac{1}{2}\frac{d}{ds}\sum\limits_{\alpha=1}^n \Big[X^{\alpha}(s)\Big]^2. \tag{2.21}\label{EqP12}$$ Эти совокупности точек образуют в ${\cal R}^n$ гиперплоскости размерности $n-2$. Огибающая множества всех таких гиперплоскостей будет образовывать границу областей однозначности и многозначности ривертона.
Огибающую области многозначности без ограничения общности можно вычислить следующим образом. Огибающая состоит из точек пересечения всех бесконечно близких гиперплоскостей при $s_1\to s_2$. Систему (\ref{EqP12}) можно разрешить относительно первых двух координат $x_1$ и $x_2$, в результате чего они становятся функциями $s_1$ и $s_2$, а так же остальных координат $x_{3},\ldots,x_{n}$: $$x_1(s_1,s_2) = \frac{G(s_2,{\bf x})n^2(s_1)-G(s_1,{\bf x})n^2(s_2)}{n^2(s_1)n^1(s_2)-n^2(s_2)n^1(s_1)},\tag{2.22}\label{EqExE}$$$$x_2(s_1,s_2) = -\frac{G(s_2,{\bf x})n^1(s_1)-G(s_1,{\bf x})n^1(s_2)}{n^2(s_1)n^1(s_2)-n^2(s_2)n^1(s_1)}.$$ Здесь $$G(s,{\bf x})=F(s)-\sum\limits_{\alpha=3}^n x^{\alpha}n^{\alpha}(s).$$ В пределе $s_1\to s_2\to s$ мы получаем уравнение гиперплоскости ${\cal E}^{n-2}(s_1,s_2)$ размерности $n-2$, являющейся пересечением двух бесконечно близких гиперплоскостей $E=E(s_1)$ и $E=E(s_2)$. В пределе $s_1\to s_2\to s_0$ получаем множество $\{{\cal E}^{n-2}(s_0)\}$ гирперплоскостей, зависящих от параметра $s_0$, образующих гиперповерхность ${\cal G}^{n-1}$, к которой касательны все гиперплоскости $E=E(s_0)$ для значений параметра $s_0$ в некотором интервале $(s_1,s_2)$. Поскольку все гиперплоскости $E=E(s)$ из интервала $s\in (s_1,s_2)$ касательны к ${\cal G}^{n-1}$, то они пересекаются друг с другом в области, лежащей в ${\cal R}^n$ с одной стороны по отношению к ${\cal G}^{n-1}$. Следовательно, гиперповерхность ${\cal G}^{n-1}$ разделяет области многозначности и однозначности ривертона, по крайней мере, для интервала $(s_1,s_2)$ параметра $s$. Переходя к пределу $s_1\to s_2\to s$ в соотношениях (\ref{EqExE}), получаем уравнения параметрического задания гиперповерхностей ${\cal G}^{n-1}$: $$x_1(s) = \frac{G'_1(s,{\bf x})}{N'_1(s)},~~x_2(s)=\frac{G'_2(s,{\bf x})}{N'_2(s)},\tag{2.23}\label{EqX1}$$ где $$G'_1(s,,{\bf x}) = \frac{d}{ds}\left(\frac{G(s,{\bf x})}{n^1(s)}\right),~~G'_2(s,{\bf x}) = \frac{d}{ds}\left(\frac{G(s,{\bf x})}{n^2(s)}\right),$$$$N'_1(s) = \frac{d}{ds}\left(\frac{n^1(s)}{n^2(s)}\right),~~N'_2(s) = \frac{d}{ds}\left(\frac{n^2(s)}{n^1(s)}\right).$$
На рис. (1)-(4) приведены примеры вычисления областей однозначности и многозначности ривертонов для размерности координатного пространства $n=2$ в случае базовых кривых:$$(1):~~ X(s) = s,~~ Y(s) = \cos(s);$$$$ (2):~~ X(s) = s+\sin(s),~~ Y(s) = \cos(s),$$$$(3):~~X(s)=s=Y(s)=1/(1+s^2).$$$$(4):~~ X(s)=s,~~Y(s)={\rm th}(s),$$ Базовые кривые выделены жирной сплошной кривой. На рисунках сплошными прямыми обозначены линии уровня $E=const$ (фронты ривертона). Фронты ортогональны базовой кривой. Области их многократного пересения и есть области многозначности решений. На эту картину фронтов накладывается динамика самой волны, которая может опрокидваться со временем вдоль прямых $E={\rm const}$.
.jpg)
$$(1):~~ X(s) = s,~~ Y(s) = \cos(s);$$
.jpg)
$$ (2):~~ X(s) = s+\sin(s),~~ Y(s) = \cos(s),$$
.jpg)
$$(3):~~X(s)=s=Y(s)=1/(1+s^2).$$
.jpg)
$$(4):~~ X(s)=s,~~Y(s)={\rm th}(s),$$
Границы областей многозначности (на рисунках обозначены жирной кривой) и задаются параметрически следующими соотношениями: $$(1):~~ X(s) = \sin(s)\cos(s)+s-2{\rm tg(s)},~~ Y(s) =-2\sin(s){\rm tg(s)},$$$$(2):~~ X(s) = s-\sin(s),~~ Y(s) = -\cos(s)-2,$$$$(3):~~ X(s)=\frac{1}{2}\frac{2s{\rm sh(s)}{\rm ch(s)}^3+{\rm ch(s)}^4+1}{{\rm ch(s)}^3{\rm sh(s)}},~~Y(s)=\frac{1}{2}\frac{-{\rm ch(s)}^4+2{\rm ch(s)}^2-3}{{\rm sh(s)ch(s)}},$$$$(4):~~X(s)=4s^3\frac{s^6+3s^4+3s^2+2}{(3s^4+2s^2-1)(s^2+1)^2},~~Y(s)=\frac{1}{6}\frac{s^8+4s^6+6s^4+14s^2-1}{(s^2+1)(s^2-1/3)}.$$
Заметим, что среди приведенных типов базовых кривых выделяется случай циклоиды под номером (2). Для этой базовой кривой граница области многозначности является вновь циклоидой, но смещенной относительно исходной по оси $y$ на $-2$ и вдоль оси $x$ - на $\pi/2$.
(5) Рисунок представляет собой анимацию решения типа ривертона для уравнения Д'Аламбера со следующей параметризацией решения:
$A_1(E)=\cos(E),~A_2(E)=\sin(E)$, $H(\xi)=(\xi^2+1)^{-1}$
2.2.2. Опрокидывание фронта
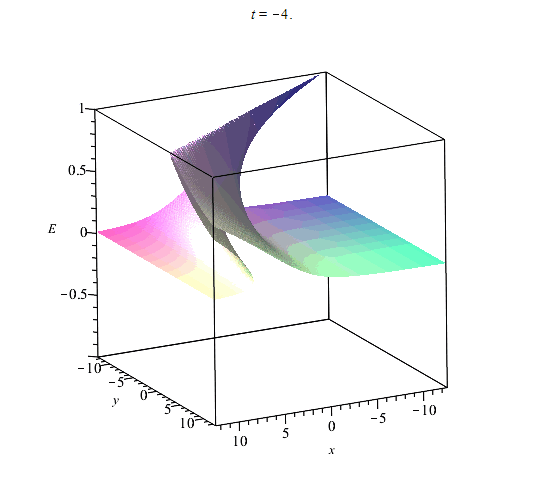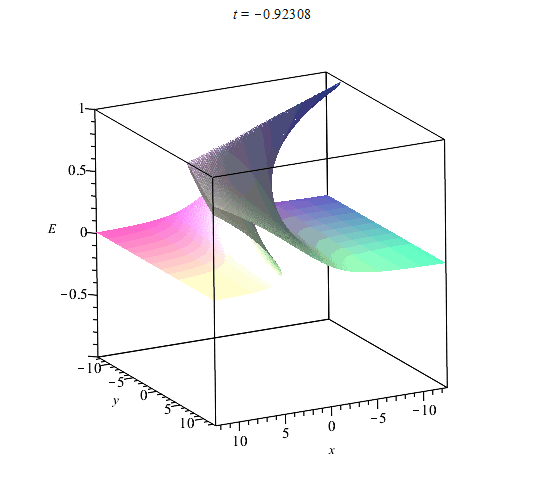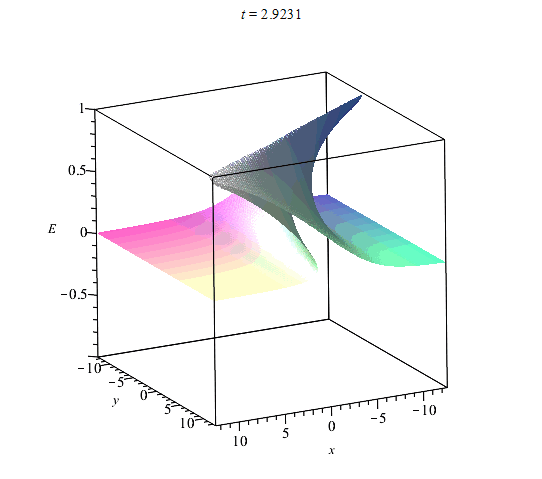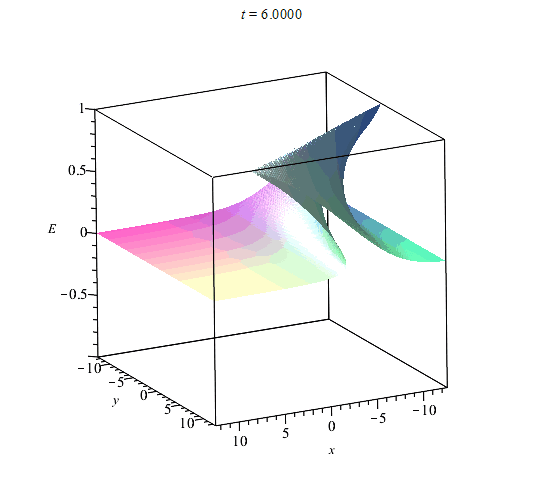
Области неоднозначности ${\cal V}^n$ - не единственная особенность ривертонов. Некоторые изоповерхности функции $E({\bf x},t)$ в ${\cal R}^n$ являются целиком поверхностями прокидывания фронта волны в соответствии со свойствами уравнения Хопфа (\ref{EqHopf}). Все точки пространства, в которых происходит опрокидывание фронта волны, определяются из условия обращения производных решения по координатам в бесконечность. По аналогии с этим мы можем найти значения параметра $s$, в которых происходит опрокидывание фронта ривертонов. Из (\ref{EqDiffH}) имеем: $$E_{,\alpha}=-\frac{A_{\alpha}H_{\eta}}{H_{\xi}+({\bf A}',{\bf x})H_{\eta}}.$$ Отсюда находим общее уравнение для поверхности опрокидывания фронта: $$H_{\xi}+({\bf A}',{\bf x})H_{\eta} = 0, ~~H(\xi,\eta)=0.$$ В области однозначности поверхность опрокидывания фронта представляет собой некоторую гиперплоскость $E=E(s_{*})$ со значением параметра $s=s_{*}$, которое находится из аналогичного соотношения для уравнения Хопфа (\ref{EqHopf}):$$s_{*}=-\frac{H_{\xi}}{R'(E(s_{*},t_{*}))},$$ где $H(\xi,\eta)$ та же функция, что и в решении {\ref{SolHd}).
Для полноты анализа укажем на следующее свойство ривертонов:
Утверждение 5. Пусть $E({\bf x},t)$ - решение (\ref{EqQLn}) в виде ривертона. Тогда любая функция $\widetilde{E}({\bf x},t)=F\Big(E({\bf x},t)\Big)$, где $F(E)$ - произвольная дважды дифференцируемая функция одного аргумента $E$, так же является ривертоном.
Доказательство. Пусть $E({\bf x},t)$ - ривертон, а $F(E)$ - произвольная дважды диифференцируемая функция. Тогда имеем следующие тождества: $$\frac{\partial F(E)}{\partial x^{\alpha}}=F'(E)E_{,\alpha}=F'(E)A_{\alpha}E_t=A_{\alpha}\frac{\partial F(E)}{\partial t}.$$ Эти соотношения соответствуют обращению в тождество уравнений (\ref{EqQLn}) при подстановке в них в качестве решения функции $\widetilde{E}({\bf x},t)=F\Big(E({\bf x},t)\Big)$.
2.3. Гиперболические, эллиптические и параболические уравнения второго порядка
Квазилинейные уравнения первого порядка играют важную роль в гидродинамике и смежных с ней разделах физики, где важную роль играют процессы переноса. Однако, как оказывается, эти уравнения играют важную роль и в теории процессов, которые описываются уравнениями в частных производных второго порядка. Учитывая, что уравнения второго порядка такие, как уравнения Максвелла, уравнения Лапласа и теплопроводности и диффузии являются уравнениями второго порядка, связь их с квазилинейными уравнениями становится важным элементом общего понимания процессов в физических системах. В данном разделе, опираясь на работы [1,2,3], представлены основные соотношения, связывающие квазилинейные уравнения первого порядка с уравнениями второго порядка двух основных типов - гиперболических и эллиптических. Связь с параболическими уравнениями будет изложена в следующих разделах.
2.3.1. Вывод уравнений второго порядка для системы $QL^{[n,1]}$
Начнем с анализа квазилинейных уравнений $QL^{[n,1]}$. Вычислим дивергенцию по пространственным координатам от обоих частей уравнения {\ref{EqQLn}). В результате находим:$$\sum\limits_{\alpha=1}^n\frac{\partial^2 E}{\partial x_{\alpha}^2}=\Delta E=\sum\limits_{\alpha=1}^n\frac{\partial}{\partial x_{\alpha}}\Big(A_{\alpha}(E)E_t\Big)= \sum\limits_{\alpha=1}^n\frac{\partial E}{\partial x_{\alpha}}\frac{dA_{\alpha}(E)}{dE}+\sum\limits_{\alpha=1}^nA_{\alpha}\frac{\partial^2E}{\partial t\partial x_{\alpha}}=$$$$= \sum\limits_{\alpha=1}^n\frac{\partial E}{\partial x_{\alpha}}\frac{dA_{\alpha}(E)}{dE}+\sum\limits_{\alpha=1}^nA_{\alpha}\frac{\partial}{\partial t}\Big(A_{\alpha}(E)E_t\Big)=2\sum\limits_{\alpha=1}^nA_{\alpha}(E)E_t\frac{dA_{\alpha}(E)}{dE}+\sum\limits_{\alpha=1}^n\Big(A_{\alpha}\Big)^2E_{tt}=$$$$=\frac{\partial}{\partial t}\left(\sum\limits_{\alpha=1}^n\Big(A_{\alpha}\Big)^2E_{t}\right)=\frac{\partial}{\partial t}\Big(|{\bf A}(E)|^2E_{t}\Big)$$
В заключении этих вычислений, получаем, что функция $E({\bf x},t)$, являющаяся решением квазилинейного уравнения первого порядка (\ref{EqQLn}), является также решением уравнения второго порядка следующего общего вида:$$\Delta E = \frac{\partial}{\partial t}\Big(|{\bf A}(E)|^2E_{t}\Big)\tag{2.24}.\label{Eq2pHn}$$
Если в этих соотношениях $E$ и ${\bf A}(E)$ - вещественные, то данное уравнение является гиперболическим и в теории электромагнитных волн известно как уравнение распространения электромагнитного излучения в диэлектрических средах с нелинейной поляризацией общего вида, но без дисперсии. Для того, что бы придать этому уравнению узнаваемую форму, введем функцию поляризации среды следующим образом:$${\cal P}(E)= c^2\left(\int |{\bf A}(E)|^2 dE - 1\right).\tag{2.25}\label{DefP}$$ В результате, уравнение (\ref{Eq2pHn}) можно переписать в стандартном для электродинамики диэлектриков виде:$$\Delta E- \frac{1}{c^2}E_{tt}=\frac{1}{c^2}\frac{\partial^2}{\partial t^2}{\cal P}(E).\tag{2.26}\label{EqEP}$$ Здесь $c$ - скорость электромагнитных волн в вакууме.
2.3.2. Важные частные случаи. Топологическое вырождение
Наиболее простым и, вместе с тем, наиболее важным частным примером полученных уравнений, связанных с квазилинейными уравнениями первого порядка типа $QL^{[n,1]}$ является уравнение Д'Аламбера. Это уравнение содержится в общем классе уравнений {\ref{Eq2pHn}) и выделяется из него условием: $$|{\bf A}(E)|^2=\sum\limits_{\alpha=1}^n A_{\alpha}^2(E)=1.\tag{2.27}\label{ConAtoDA}$$ Поскольку функциональная зависимость векторного поля ${\bf A}(E)$ от $E$ произвольна, то любое векторное поле единичной длины, параметрически зависящее от $E$ будет удовлетворять этому условию в размерности $n>1$. Например, в двумерном случае поле ${\bf A}(E)$ может быть параметризовано без ограничения общности следующим способом:$$A_{1}(E)=\cos\Phi(E),~~A_2(E)=\sin\Phi(E),\tag{2.28}\label{DefAn2}$$ где $\Phi(E)$ - произвольная дифференцируемая функция $E$. В трехмерном случае в общей параметризации участвует уже две произвольных функции $\Phi(E)$ и $\Theta(E)$: $$A_{1}(E)=\cos\Phi(E)\sin\Theta(E),~~A_2(E)=\sin\Phi(E)\sin\Theta(E),~~A_3(E)=\cos\Theta(E).\tag{2.29}\label{DefAn3}$$
С увеличением размерности число свободных параметров общего допустимого представления ${\bf A}(E)$ растет и, как не трудно видеть, равно $n-1$. Это означает, что уравнение Д'Аламбера:$$\Delta E- E_{tt}=0\tag{2.30}\label{EqDA}$$ имеет решения в форме ривертонов следующего вида:$$E=H\Big(t+({\bf A}(E),{\bf x})\Big).\tag{2.31}\label{SolDA}$$ Множество всех неэквивалентных решений определяется множеством всех возможных неэквивалентных параметризаций единичного векторного поля, которое совпадает с множеством всех отображений сферы ${\cal S}^{n-1}$ в себя. Поскольку уравнение Д'Аламбера является линейным, то множество параметризаций единичного векторного поля в ${\cal R}^n$ и, соответственно, множество всех отображений сферы ${\cal S}^{n-1}$ в себя, определяет степень вырожденности решений. Такой тип вырождения в дальнейшем мы будем называть топологическим вырождением. Задача перечисления всех отображения ${\cal S}^{n-1}$ в себя относится к топологии и ее обсуждение относим к соответствующим монографиям и учебникам по топологии.
Важным результатом найденной связи между уравнением (\ref{EqDA}) и (\ref{EqQLn}) является вывод, что уравнения Д'Аламбера при некоторых условиях, которые будут обсуждаться далее, допускает распространение электромагнитного излучения вдоль достаточно произвольных кривых - базовых кривых ривертона. Забегая вперед можно сказать, что такое распространение волн можно организовать задавая определенным образом граничные условия на некоторых поверхностях, ассоциированных с поверхностями раздела между областями многозначности и однозначности. Здесь мы лишь обратим внимание на тот факт, что в отличие от всех других типов уравнений (\ref{Eq2pHn}), уравнение Д'Аламбера содержит решения типа ривертонов, у которых отсутствует явление опрокидывания фронта. Действительно, как следует из утверждения 4, уравнение динамики волны вдоль базовой кривой для уравнения Д'Аламбера имеет вид:$$\frac{\partial E}{\partial s}=\frac{\partial E}{\partial t},$$ что соответствует простой линейной волне, распространяющейся вдоль базовой кривой с параметром вдоль кривой $s$.
С увеличением размерности число свободных параметров общего допустимого представления ${\bf A}(E)$ растет и, как не трудно видеть, равно $n-1$. Это означает, что уравнение Д'Аламбера:$$\Delta E- E_{tt}=0\tag{2.30}\label{EqDA}$$ имеет решения в форме ривертонов следующего вида:$$E=H\Big(t+({\bf A}(E),{\bf x})\Big).\tag{2.31}\label{SolDA}$$ Множество всех неэквивалентных решений определяется множеством всех возможных неэквивалентных параметризаций единичного векторного поля, которое совпадает с множеством всех отображений сферы ${\cal S}^{n-1}$ в себя. Поскольку уравнение Д'Аламбера является линейным, то множество параметризаций единичного векторного поля в ${\cal R}^n$ и, соответственно, множество всех отображений сферы ${\cal S}^{n-1}$ в себя, определяет степень вырожденности решений. Такой тип вырождения в дальнейшем мы будем называть топологическим вырождением. Задача перечисления всех отображения ${\cal S}^{n-1}$ в себя относится к топологии и ее обсуждение относим к соответствующим монографиям и учебникам по топологии.
Важным результатом найденной связи между уравнением (\ref{EqDA}) и (\ref{EqQLn}) является вывод, что уравнения Д'Аламбера при некоторых условиях, которые будут обсуждаться далее, допускает распространение электромагнитного излучения вдоль достаточно произвольных кривых - базовых кривых ривертона. Забегая вперед можно сказать, что такое распространение волн можно организовать задавая определенным образом граничные условия на некоторых поверхностях, ассоциированных с поверхностями раздела между областями многозначности и однозначности. Здесь мы лишь обратим внимание на тот факт, что в отличие от всех других типов уравнений (\ref{Eq2pHn}), уравнение Д'Аламбера содержит решения типа ривертонов, у которых отсутствует явление опрокидывания фронта. Действительно, как следует из утверждения 4, уравнение динамики волны вдоль базовой кривой для уравнения Д'Аламбера имеет вид:$$\frac{\partial E}{\partial s}=\frac{\partial E}{\partial t},$$ что соответствует простой линейной волне, распространяющейся вдоль базовой кривой с параметром вдоль кривой $s$.
2.3.3. Вывод уравнений второго порядка для системы $QL^{[n,m]}$
Из системы уравнений (\ref{EqQLnm}) в результате дифференцирования находим: $$\sum\limits_{\alpha=1}^n\frac{\partial^2}{\partial (x^\alpha)^2}E=\Delta E=\sum\limits_{\alpha=1}^n\sum\limits_{a=1}^m\frac{\partial}{\partial x^{\alpha}}\left(A^a_{\alpha}(E)\frac{\partial E}{\partial y^a}\right).$$ Используя повторно сами уравнения (\ref{EqQLnm}) в правой части этого соотношения, приходим к общему уравнению следующего вида:$$\Delta E = \sum\limits_{a=1}^m\sum\limits_{b=1}^m\frac{\partial}{\partial y^a}\left(R^{ab}(E)\frac{\partial E}{\partial y^b}\right),\tag{2.31}\label{EqE}$$ где: $$R^{ab} = \sum\limits_{\alpha=1}^n A^a_{\alpha}(E)A^b_{\alpha}(E).\tag{2.32}\label{DefbR}$$ Заметим, что в силу зависимости $R^{ab}(E)$ только от $E$, выполняются следующие соотношения: $$\frac{\partial}{\partial y^a}\left(R^{ab}(E)\frac{\partial E}{\partial y^b}\right)=\frac{\partial}{\partial y^b}\left(R^{ab}(E)\frac{\partial E}{\partial y^a}\right),~~a\not=b.$$ Это является полезным свойством уравнений при анализе числа их неэквивалентных решений, о чем речь пойдет далее.
Утверждение 3. Каждое решение системы квазилинейных уравнений (\ref{EqQLnm}) в форме неявного алгебраического уравнения (2.12) для фиксированного выбора $R^{ab}(E)$ при соответствующем произвольном выборе функций $A^a_{\alpha}(E)$ является решением уравнения (\ref{EqE}). Обратное утверждение неверно.
2.3.4. Классификация неэквивалентных решений уравнений второго порядка
Общий анализ связи различных систем $QL^{{n,m}}$ с соответствующими им уравнениями второго порядка показывает, что одно и тоже уравнение второго порядка может иметь несколько различных типов решений, которые определяются различными по размерности системами $QL^{{n,m}}$. Это ставит задачу выяснения условий существования различных не эквивалентных типов решений в неявной форме (\ref{SolHnm}) уравнений второго порядка и перечислением всех таких решений.
Эта задача состоит из двух подзадач. Первая из них сводится к выяснению числа свободных функциональных параметров матриц $A^a_{\alpha}(E)$ системы $QL^{(n,m)}$, от которых не зависит вид матрицы $R^{ab}$ уравнения второго порядка. Вторая подзадача состоит в выяснении числа всех возможных редукций функциональных параметров $A^a_{\alpha}(E)$ системы $QL^{(n,m)}$, которые переводят эту систему в другую систему $QL^{(k,l)}$ той же полной координатной размерности $N=n+m=k+l$, как это было продемонстрировано в случае уравнений типа Д'Аламбера в размерности $4=3+1$.
Утверждение 4. При заданной общей координатной размерности пространства $N=n+m$ уравнение второго порядка (\ref{EqE}) системы $QL^{(n,m)}$ будет иметь различные неэквивалентные решения, соответствующие различным неэквивалентным функциональным параметрам $A^a_{\alpha}(E)$ только при условии $m < 2n-1$ или $(N+1)/3 < n$. Число свободных функциональных параметров при выполнении этого условия будет равно $M=(2n-1-m)m/2=(3n-N-1)(N-n)/2$. В случае $M\le 0$ уравнение второго порядка определяется единственным образом с помощь функциональных параметров $A^a_{\alpha}(E)$.
Доказательство. Сформулированное утверждение доказывается сравнением размерностей матриц $R^{ab}$ и $A^a_{\alpha}$. Для системы $QL^{(n,m)}$ число независимых компонент $R^{ab}$ матрицы ${\bf R}$ в силу ее симметричности равно $m(m+1)/2$, а размерность числа компонент $A^a_{\alpha}$ матрицы ${\bf A}$ равна $n\times m$. Следовательно, свободные функциональные параметры в определении матрицы $A^a_{\alpha}$ по сравнению с матрицей $R^{ab}$ будут только в том случае, если $m < 2n-1$. Число свободных функциональных параметров $A^a_{\alpha}$ будет в этом случае определяться разностью между размерностями матриц ${\bf R}$ и ${\bf A}$. Эта величина равна $M=mn-m(m+1)/2=(2n-m-1)m/2=(3n-N-1)(N-n)/2$. Если $M<0$, то свободные параметры отсутствуют и матрица ${\bf R}$ однозначно определяется функциональными параметрами $A^a_{\alpha}(E)$.
Так, например, для системы $QL^{(3,1)}$ имеем $M=2>0$, т.е. для одного и того же уравнения второго порядка имеется бесконечное число неэквивалентных решений, которые определяются двумя свободными параметрами, что и было продемонстрировано в [ZhTMF13]. Для исследуемой далее системы $QL^{(2,2)}$ $M=1>0$ неэквивалентные решения определяются одним свободным функциональным параметром. Для системы $QL^{(3,2)}$ число свободных функциональных параметров равно $M=4$ и т.д..
Рассмотрим теперь вопрос о редукциях уравнений второго порядка системы $QL^{(k,l)}$ к идентичным уравнениям второго порядка системы $QL^{(n,m)}$ при условии, что размерности координатного пространства связаны условием $n+m \le k+l$. Смысл редукции состоит в том, чтобы с помощью специального выбора функциональных параметров $A^a_{\alpha}(E)$ системы $QL^{(k,l)}$ редуцировать уравнение второго порядка меньшей размерности координатного пространства или той же размерности, но со структурой матрицы, соответствующей другой системе $QL^{(n,m)}$. Существование не тривиальных редукций так же связано с наличием свободных функциональных параметров. Однако в случае редукций трудно дать полное описание всех таких возможных вариантов, поскольку тип редукции определяется не только исходной системой, но и типом уравнения, к которому система редуцируется. Поэтому удобнее процедуру редукций описать на конкретных примерах.
2.3.5. Система $QL^{(2,2)}$ и ее редукции
Рассмотрим в качестве важного примера систему $QL^{(2,2)}$ в следующем виде: $$\frac{\partial E}{\partial x}=A(E)\frac{\partial E}{\partial z}+B(E)\frac{\partial E}{\partial t},\tag{2.33}\label{EqPR}$$$$\frac{\partial E}{\partial y}=C(E)\frac{\partial E}{\partial z}+D(E)\frac{\partial E}{\partial t}.$$ Коэффициенты этой системы $A^{a}_{\alpha}$ имеют вид: $$A^{1}_1=A(E),~A^{2}_1=B(E),~A^{1}_2=C(E),~A^{2}_2=D(E).$$ Решения этой системы можно найти из общего интеграла : $$H(E,z+\Phi(E,x,y),t+\Psi(E,x,y))=0,$$ где $$ \Phi(E,x,y)=A(E)x+C(E)y,~~\Psi(E,x,y)=B(E)x+D(E)y.$$ Матрица ${\bf R}$ для этой системы будет иметь следующий вид: $$R^{11}=\Big(A^{1}_1\Big)^2+\Big(A^{1}_2\Big)^2=A^2(E)+C^2(E),$$$$ R^{22}=\Big(A^{2}_1\Big)^2+\Big(A^{2}_2\Big)^2=B^2(E)+D^2(E),$$$$R^{21}=R^{12}=A^{1}_1A^{2}_1+A^{1}_2A^{2}_2=A(E)B(E)+C(E)D(E).$$ Уравнение второго порядка, cоответствующее этой матрице, имеет вид: $$\frac{\partial^2 E}{\partial x^2}+\frac{\partial^2 E}{\partial y^2} =\tag{2.34}\label{EqES22}$$$$=\frac{\partial}{\partial z}\left( R^{11}(E) \frac{\partial E}{\partial z}\right)+\frac{\partial}{\partial t} \left(R^{22}(E) \frac{\partial E}{\partial t}\right)+2\frac{\partial}{\partial z} \left(R^{12}(E) \frac{\partial E}{\partial t}\right).$$ Записанное в таком виде уравнение второго порядка появляется в математической физике редко. Поэтому интересны ситуации, когда это уравнение в результате определенной редукции переходит в уравнения, встречающиеся на практике чаще. Примером таких уравнений являются уравнения распространения электромагнитных волн в диэлектриках без дисперсии или акустических волн в газе. Решения этих уравнений, как было показано в [ZhTMF13], в соответствии с введенными выше обозначениями, относятся к системам $QL^{(3,1)}$. Поэтому интерес представляют редукции системы $QL^{(2,2)}$ к системам $QL^{(3,1)}$. Такой интерес в первую очередь вызван тем, что решения систем $QL^{(2,2)}$ определяются интегралами (\ref{SolHnm}) с двумя независимыми аргументами, в то время как $QL^{(3,1)}$ только с одним. Это означает, что функциональный класс решений, которые могут быть получены с помощью систем $QL^{(2,2)}$, значительно шире, чем с помощью систем $QL^{(3,1)}$.
Необходимая редукция $QL^{(2,2)}$, приводящая к уравнениям второго порядка, связанных системами $QL^{(3,1)}$, соответствует следующим условиям: $$R^{12}=R^{21}=A(E)B(E)+C(E)D(E)=0.\tag{2.35}\label{EqR12}$$ Если это условие выполнено, то уравнение (\ref{EqES22}) принимает следующий вид: $$\frac{\partial^2 E}{\partial x^2}+\frac{\partial^2 E}{\partial y^2}=\frac{\partial^2 Q(E)}{\partial z^2}+\frac{\partial^2 P(E)}{\partial t^2},$$ где: $$\frac{dQ}{dE}=R^{11}(E),~~\frac{dP}{dE}=R^{22}(E).$$ При дополнительном условии: $$R^{11}=A^2(E)+C^2(E)=-1,\tag{2.36}\label{EqR11}$$ уравнение (\ref{EqES22}) превращается в уравнение: $$\frac{\partial^2 E}{\partial x^2}+\frac{\partial^2 E}{\partial y^2}+\frac{\partial^2 E}{\partial z^2}=\frac{\partial^2 P(E)}{\partial t^2},\tag{2.37}\label{EqES31}$$ которое совпадает по форме с уравнением (2.26) для системы $QL^{(3,1)}$ (\ref{EqQLn}) с $n=3$, которая подробно рассматривалась в [ZhTMF13]. Как отмечалось в [ZhTMF13], уравнение (\ref{EqES31}) представляет собой уравнение распространения электромагнитных волн в среде с нелинейной поляризацией без дисперсии. Условия (\ref{EqR12}) и (\ref{EqR11}) выполняются автоматически, если функции $A,B,C$ имеют следующий общий вид: $$A(E)=i\cos\Big(\chi(E)\Big),~C(E)=i\sin\Big(\chi(E)\Big),\tag{2.38}\label{SolABCI}$$$$B(E)=-D(E){\rm tg}\Big(\chi(E)\Big).$$ Другой вариант выполнения условий (\ref{EqR12}) и (\ref{EqR11}) такой: $$A(E)={\rm sh}\Big(\chi(E)\Big),~C(E)=i{\rm ch}\Big(\chi(E)\Big),\tag{2.39}\label{SolABCII}$$$$B(E)=-iD(E){\rm cth}\Big(\chi(E)\Big).$$ При этом функции $D(E)$ и $\chi(E)$ остаются произвольными. В случае (\ref{SolABCI}):$$\frac{dP(E)}{dE}=\frac{D^2(E)}{\cos^2\Big(\chi(E)\Big)},$$ соответственно, в случае (\ref{SolABCII}): $$\frac{dP(E)}{dE}=-\frac{D^2(E)}{{\rm sh}^2\Big(\chi(E)\Big)}.$$ В отличие от интеграла (\ref{SolHd}) системы $QL^{(31)}$, интеграл (\ref{SolHnm}), соответствующий системе $QL^{(2,2)}$ при выполнении условий (\ref{EqR12}) и (\ref{EqR11}) будет иметь более общий вид. Для варианта (\ref{SolABCI}): $$H\Big(E,z+i\Big[\cos(\chi(E))x+\sin(\chi(E))y\Big],t+D(E)\Big[(x {\rm tg}(\chi(E))+y\Big]\Big)=0.$$ и для варианта (\ref{SolABCII}):$$H\Big(E,z+{\rm sh}(\chi(E))x+i{\rm ch}(\chi(E))y,t+D(E)\Big[-i x{\rm cth}(\chi(E))+y\Big]\Big)=0.$$
Эти соотношения представляют собой наиболее общий функциональный вид интегралов для уравнения (\ref{EqES31}), что существенно расширяет класс решений этих уравнений. Однако, в отличие от решений рассмотренных в [ZhTMF13], решения, соответствующие этим интегралам, являются, вообще говоря, комплексными. Такие решения в конечном итоге оказываются аналогичными решениям комплексных уравнений типа $QL^{(3,1)}$, рассмотренными в [ZhSTF13].
2.3.6. Уравнение Д'Аламбера в размерности 3+1. Решение Кассандрова
Частным случаем системы (\ref{EqES31}) является уравнение Д'Аламбера, которое соответствует следующему выбору элементов матрицы ${\bf R}$: $$ R^{11}=A^2(E)+C^2(E)=-1,~R^{22}=B^2(E)+D^2(E)=1,\tag{2.40}\label{EqRDA}$$$$R^{12}=R^{21}=A(E)B(E)+C(E)D(E)=0,$$ В этом случае $P(E)=1$ и уравнение (\ref{EqES31}) примет: $$\frac{\partial^2 E}{\partial x^2}+\frac{\partial^2 E}{\partial y^2}+\frac{\partial^2 E}{\partial z^2}=\frac{\partial^2 E}{\partial t^2}.$$ Соответствующий (\ref{EqRDA}) функциональный вид коэффициентов $A,B,C,D$ можно записать в такой форме: $$A(E)=i\cos\Big(\chi(E)\Big),~~C(E)=i\sin\Big(\chi(E)\Big),\tag{2.41}\label{SolABCId}$$$$B(E)=\sin\Big(\chi(E)\Big),~~D(E)=-\cos\Big(\chi(E)\Big).$$ Функция $\chi(E)$ - произвольна.
Эти соотношения приводят к следующему интегралу: $$H\Big(E,z+i[\cos(\chi(E))x+\sin(\chi(E))y],t+x \sin(\chi(E))-y\cos(\chi(E))\Big)=0.$$ По аналогии с (\ref{SolABCII}) можно получить интеграл с гиперболическими функциями от произвольной функции $\chi(E)$.
Эти соотношения приводят к следующему интегралу: $$H\Big(E,z+i[\cos(\chi(E))x+\sin(\chi(E))y],t+x \sin(\chi(E))-y\cos(\chi(E))\Big)=0.$$ По аналогии с (\ref{SolABCII}) можно получить интеграл с гиперболическими функциями от произвольной функции $\chi(E)$.
Интерес представляет особое решение Кассандрова, которое дает эффективные результаты в построении метрик Пенроуза-Риндлера. (В статье [ZhТМФ16], хотя я и сослался на работу В.Касаандрова, но не совсем правильно назвал, полученное им решение решением Пенроуза-Риндлера. В реальности решение получил именно В.Кассандров. В дальнейшем исправлю эту неточность в дургих работах.-Журавлев В.М.) Это решение соответствует специальному выбору элементов матрицы ${\bf R}$. Именно, рассмотрим матрицу следующего вида: $$R^{11}=A^2(E)+C^2(E)=0,~R^{22}=B^2(E)+D^2(E)=0,\tag{2.42}\label{EqRDAyy}$$$$R^{12}=R^{21}=A(E)B(E)+C(E)D(E)=1.$$ Соответствующие этим соотношениям функции $B,C,D$ можно выбрать так: $$C(E)=iA(E),~~D(E)=-iB(E),~~B(E)=A^{-1}(E)/2.$$ При этом функция $A(E)$ - произвольна. Соответствующий интеграл можно записать в виде: $$H\Big(E,u+A(E)(x+iy),v+2(x-iy)/A(E)\Big)=0.$$ или $$H\Big(E,u+A(E)(x+iy),A(E)v+2(x-iy)\Big)=0.\tag{2.43}\label{EqIntPR}$$ Уравнение второго порядка в этом случае принимает следующую форму: $$ \frac{\partial^2 E}{\partial x^2}+\frac{\partial^2 E}{\partial y^2}=2\frac{\partial^2 E}{\partial u\partial v},$$ что эквивалентно уравнению Д'Аламбера в конусных переменных $u=z+t,~v=z-t$. Интеграл (\ref{EqIntPR}) представляет собой обобщенный интеграл Кассандрова [Каs], который переходит в точности в интеграл Кассандрова в случае $A(E)=E$.
2.3.7. Системы $QL^{(n,m)}$ и уравнения Лапласа
На примере системы $QL^{(2,2)}$ рассмотрим другой тип редукций, который позволяет в качестве одного из вариантов уравнения второго порядка получить уравнение Лапласа в размерностях $d=2$ и $d=3$. Поскольку число свободных функциональных параметров системы $QL^{(2,2)}$ равно $M=1$, то вырожденная система уравнений на элементы матрицы ${\bf R}$:$$R^{11}=A^2(E)+C^2(E)=0,~R^{22}=B^2(E)+D^2(E)=0,\tag{2.44}\label{EqRDA20}$$$$R^{12}=R^{21}=A(E)B(E)+C(E)D(E)=0,$$ имеет нетривиальное решение:$$C(E)=iA(E),~~D(E)=iB(E),$$
содержащее два свободных функциональных параметра $A(E)$ и $B(E)$. Соответствующий интеграл принимает такой вид:$$H\Big(E,z+A(E)(x+iy),t+B(E)(x+iy)\Big)=0.\tag{2.45}\label{IntL22}$$ Решения этого уравнения удовлетворяют уравнению Лапласа: $$\frac{\partial^2 E}{\partial x^2}+\frac{\partial^2 E}{\partial y^2}=0.\tag{2.46}\label{EqLap2}$$
содержащее два свободных функциональных параметра $A(E)$ и $B(E)$. Соответствующий интеграл принимает такой вид:$$H\Big(E,z+A(E)(x+iy),t+B(E)(x+iy)\Big)=0.\tag{2.45}\label{IntL22}$$ Решения этого уравнения удовлетворяют уравнению Лапласа: $$\frac{\partial^2 E}{\partial x^2}+\frac{\partial^2 E}{\partial y^2}=0.\tag{2.46}\label{EqLap2}$$
- Войдите на сайт для отправки комментариев
- 4795 просмотров
