Данный пост представляет собой методическую зарисовку на тему дифференциальных уравнений движения материальной точки в полярной системе координат.
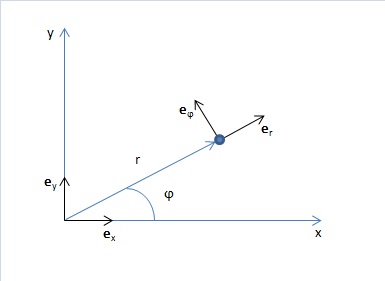 Рис. 1.
Рис. 1.
Как известно, движение материальной точки описывается векторным уравнением:
$m\boldsymbol{a}=\boldsymbol{F}$ (1)
Векторы $\boldsymbol{a}$ и $\boldsymbol{F}$ могут быть заданы своими координатами как в декартовом базисе $(\boldsymbol{e}_x, \boldsymbol{e}_y )$, так и в полярном базисе$(\boldsymbol{e}_r, \boldsymbol{e}_\varphi )$.
Покажем связь декартовой и полярной системы координат:
$\boldsymbol{e}_r = (~~\cos\varphi,\sin\varphi)$
$\boldsymbol{e}_\varphi = (-\sin\varphi,\cos\varphi)$ (2)
Проекция произвольного вектора на координатную ось задается скалярным произведением:
$\boldsymbol{V}_r = \boldsymbol{V}\cdot \boldsymbol{e}_r$
$\boldsymbol{V}_\varphi= \boldsymbol{V}\cdot \boldsymbol{e}_\varphi$ (3)
Откуда непосредственно следует:
$x=r\cos\varphi$
$y=r\sin\varphi$ (4)
что в случае радиус-вектора точки достаточно очевидно.
Чтобы добраться до ускорения точки в полярных координатах, займемся дифференцированием и найдем сначала скорость:
$\dot{x}=\dot{r}\cos\varphi-r\dot{\varphi}\sin\varphi$
$\dot{y}=\dot{r}\sin\varphi+r\dot{\varphi}\cos\varphi$ (5)
Теперь мы знаем координаты вектора скорости в декартовом базисе:
$\boldsymbol{\upsilon} =(\dot{x},\dot{y})$ (6)
Снова обратимся к формулам (3) и получим координаты вектора скорости в полярном базисе:
$\boldsymbol{\upsilon} =(\dot{r},r\dot{\varphi})$ (7)
Продолжим дифференцировать, чтобы найти ускорение точки:
$\ddot{x}=\ddot{r}\cos\varphi-2\dot{r}\dot{\varphi} \sin\varphi -r\ddot{\varphi}\sin\varphi -r\dot\varphi^2\cos\varphi \\ \ddot{y}=\ddot{r}\sin\varphi+2\dot{r}\dot{\varphi} \cos\varphi +r\ddot{\varphi}\cos\varphi -r\dot\varphi^2\sin\varphi$ (8)
Приводя подобные слагаемые, получим:
$\ddot{x}= (\ddot{r}- r\dot\varphi^2) \cos\varphi - (r\ddot{\varphi}+2\dot{r}\dot{\varphi})\sin\varphi \\ \ddot{y}= (\ddot{r}- r\dot\varphi^2) \sin\varphi + (r\ddot{\varphi}+2\dot{r}\dot{\varphi})\cos\varphi$ (9)
И снова используем (3) теперь уже для расчета ускорения. Получаем вектор ускорения точки в полярной системе координат:
$\boldsymbol{a} =(\ddot{r}- r\dot\varphi^2, r\ddot{\varphi}+2\dot{r}\dot{\varphi})$ (10)
Воспользуемся полученными результатами для расчета движения материальной точки в центральном гравитационном поле. Рассмотрим вектор силы притяжения в полярном базисе:
$\boldsymbol{F} =(-\frac{\mu m}{r^2},0)$, (11)
где $\mu$ - гравитационный параметр центрального тела.
Запишем систему дифференциальных уравнений движения точки:
$\left\{\begin{array}{lcl} ma_r=F_r\\ ma_\varphi=F_\varphi \end{array}\right. $ (12)
Массу можно сократить:
$\left\{\begin{array}{lcl} \ddot{r}- r\dot\varphi^2&=&-\frac{\mu}{r^2}\\ r\ddot{\varphi}+2\dot{r}\dot{\varphi}&=&0 \end{array}\right.$ (13)
В такой записи очень удобно вводить дополнительные ускорения. Рассмотрим пример. Пусть спутник движется по круговой орбите на высоте 200 км. Дополнительное радиальное ускорение 0.01 м/с2 в течение 1 часа не приведет к подъему высоты орбиты, а лишь даст ей небольшой эксцентриситет (Рис. 2).
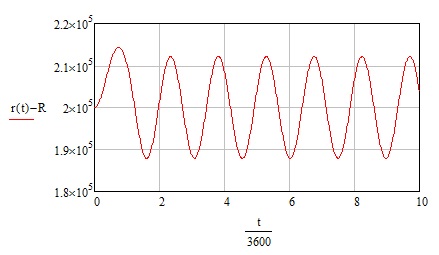 Рис. 2.
Рис. 2.
Такое же по величине ускорение в трансверсальном направлении поднимет орбиту на 60 км и сделает ее эллиптической (Рис. 3).
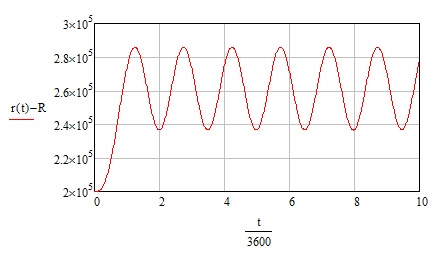 Рис. 3.
Рис. 3.
А что произойдет, если дополнительное ускорение будет действовать достаточно долго? Решим уравнения (13) с добавочным трансверсальным ускорением $ a_t $ и посчитаем энергетику процесса.
$\left\{\begin{array}{lcl} \ddot{r}- r\dot\varphi^2&=&-\frac{\mu}{r^2}\\ r\ddot{\varphi}+2\dot{r}\dot{\varphi}&=&a_t \end{array}\right.$ (14)
Кинетическая энергия тела равна $T=\frac{1}{2}m(\dot{r}^2+r^2\dot{\varphi}^2$), потенциальная энергия тела равна $U=-\frac{\mu m}{r}$, а полная энергия равна их сумме.
Оказывается, не смотря на все усилия двигателя, кинетическая энергия будет уменьшаться (парадокс спутника) [1]. При этом полная энергия будет расти, пока не достигнет нулевой отметки (еще один парадокс ![]() ) (Рис.4). Тело достигнет параболической скорости на данной высоте и будет готово покинуть сферу действии центрального тела. Произойдет это на восьмые сутки полета.
) (Рис.4). Тело достигнет параболической скорости на данной высоте и будет готово покинуть сферу действии центрального тела. Произойдет это на восьмые сутки полета.
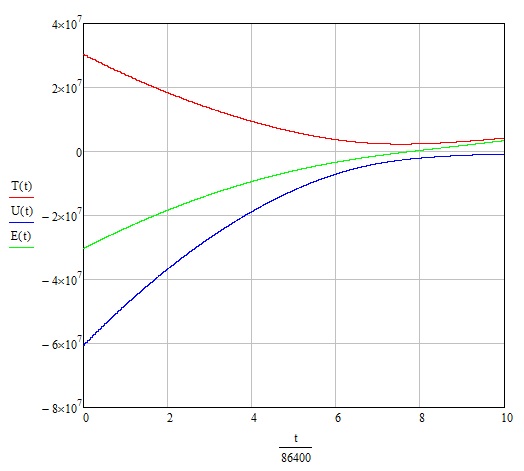 Рис. 4.
Рис. 4.
Обратимся теперь к Луне.
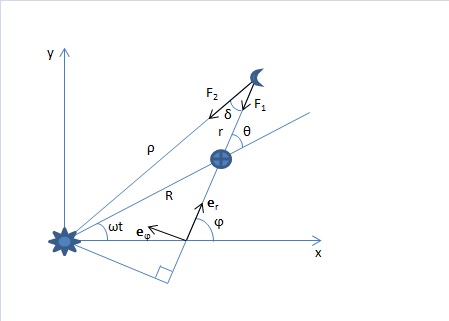 Рис. 5.
Рис. 5.
Допустим, Земля движется по круговой орбите радиуса $R$. Тогда скорость Луны складывается из двух скоростей: скорости движения центра Земли $\boldsymbol{\upsilon_1}$ и скорости движения относительно центра Земли $\boldsymbol{\upsilon_2}$.
$\boldsymbol{\upsilon_m}=\boldsymbol{\upsilon_1}+\boldsymbol{\upsilon_2}$ (15)
Выпишем координаты этих векторов в полярном базисе:
$\boldsymbol{\upsilon_1}=(R\omega\sin\theta, R\omega\cos\theta)$ (16)
$\boldsymbol{\upsilon_2}=(\dot{r},r\dot{\varphi})$ (17)
Возводя в квадрат векторное равенство (15), получим квадрат скорости Луны, а затем и ее кинетическую энергию.
$ \upsilon_{m}^2=\upsilon_{1}^2+\upsilon_{2}^2+2\, \boldsymbol{\upsilon_1} \cdot \boldsymbol{\upsilon_2} $ (18)
$T=\frac{1}{2} m (R^2\omega^2+\dot{r}^2+r^2 \dot{\varphi}^2+R\omega\sin\theta\, \dot{r}+R\omega\cos\theta r\dot{\varphi})$ , (19)
где $m$ - масса Луны.
Найдем ускорение Земли относительно Солнца, продифференцировав компоненты ее скорости (16):
$\boldsymbol{a_1}=(-R\omega^2\cos\theta,R\omega^2\sin\theta)$ (20)
Ускорение Луны относительно центра Земли можно найти по уже известной формуле (10):
$\boldsymbol{a_2} =(\ddot{r}- r\dot\varphi^2, r\ddot{\varphi}+2\dot{r}\dot{\varphi})$. (21)
Полное ускорение Луны равно сумме $\boldsymbol{a_1}$ и $\boldsymbol{a_2}$.
Перейдем к силам, действующим на Луну. Их две: сила притяжения Земли $\boldsymbol{F_1}$ и сила притяжения Солнца $\boldsymbol{F_2}$.
Проекции этих сил на полярные оси таковы:
$\boldsymbol{F_1}=(-\frac{\mu m}{r^2},0)$
$\boldsymbol{F_2}=(-\frac{\lambda m}{\rho^2}cos\delta, \frac{\lambda m}{\rho^2}sin\delta)$ (22)
где $\mu$ - гравитационный параметр Земли,
$\lambda$ - гравитационный параметр Солнца,
$ \rho^2=R^2+r^2+2Rrcos\theta$ - расстояние от Луны до Солнца,
$\delta$ - угол между направлениями на центр Земли и центр Солнца.
Геометрические построения (Рис. 5) показывают, что
$\rho \cos\delta=r+R\cos\theta$
$\rho \sin\delta=R\sin\theta$ (23)
В итоге мы имеем уравнения движения Луны:
$\left\{\begin{array}{lcl} \ddot{r}- r\dot\varphi^2-R\omega^2\cos\theta&=&-\frac{\mu}{r^2}-\frac{\lambda}{\rho^2}cos\delta\\r\ddot{\varphi}+2\dot{r}\dot{\varphi}+ R\omega^2\sin\theta &=&\frac{\lambda}{\rho^2}sin\delta\end{array}\right.$ (24)
Потенциальная энергия Луны в этих обозначениях равна:
$U=-\frac{\mu m}{r}-\frac{\lambda m}{\rho}$ (25)
Полученный выше вывод уравнений движения Луны, на мой взгляд, весьма прост и нагляден. Численное решение этих уравнений дает качественную картину движения Луны. Выписанные в такой форме уравнения удобны для исследования возмущаюющих сил, которые просто добавляются в правую часть (24).
Известно, что Луна удаляется от Земли. Механизм, отвечающий за этот процесс, достаточно прост. Приливные явления создают небольшое трансверсальное ускорение Луны. Источником энергии служит осевое вращение Земли. Земля отдает энергию вращения Луне, а та удаляется. По мере удаления приливные явления ослабевают. На какую высоту Земля может загнать Луну, пока не прекратится действие приливных сил или пока Земля не израсходует весь запас энергии осевого вращения, и что будет потом?
С помощью уравнений (24) можно оценить величину трансверсальной силы, которая поднимает орбиту Луны на 38 мм в год.
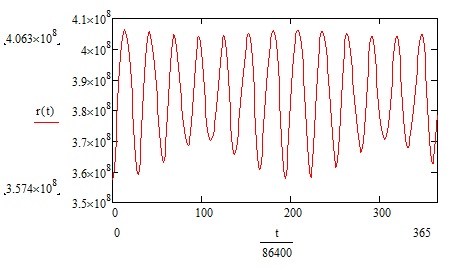 Рис. 6.
Рис. 6.
На Рис. 6 показана зависимость расстояния Земля-Луна на протяжении года. Среднее расстояние найдем по формуле:
$r_m=\frac{1}{T}\int_{0}^{T}r(t)dt$ (26)
Теперь подберем такое добавочное ускорение в правой части второго уравнения системы (24), чтобы среднее за год расстояние Земля-Луна увеличилось на принятые сейчас 38 мм.
Оказывается, что это ускорение должно быть равно $3\cdot10^{-15}$ м/c2 , а сила соответственно должна быть равна $2.204\cdot10^8$ Н.
Теперь нужно понять, какая часть мирового океана должна быть вовлечена в приливные вздутия, чтобы создать такую силу.
Заменим приливные вздутия двумя эквивалентными точечными массами на противоположных сторонах Земли, и пусть прямая, соединяющая эти точки составляет угол $\delta$ с радиус вектором направленным от центра Земли к центру Луны (Рис. 7)
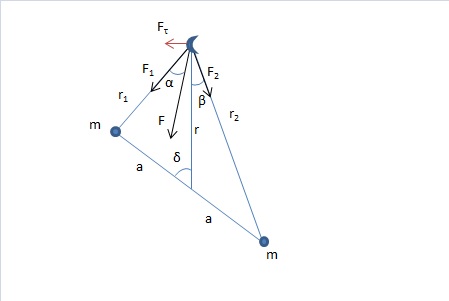 Рис. 7.
Рис. 7.
Трансверсальная компонента силы $F$ равна:
$F_{\tau}=-F_1\sin\alpha+F_2\sin\beta$ (27)
Используя теорему синусов, найдем углы $\alpha$ и $\beta$
$\sin\alpha=\frac{a\sin\delta}{r_1}$
$\sin\beta=\frac{a\sin\delta}{r_2}$ (28)
Соответственно силы притяжения равны:
$F_1 =-\frac{\nu m}{r_1^2}$
$F_2 =-\frac{\nu m}{r_2^2}$ (29)
где $\nu$ - гравитационный параметр Луны.
Подставляя (28) и (29) в (27), получим:
$F_{\tau}=-\nu m a \sin\delta(\frac{1}{r_1^3}-\frac{1}{r_2^3})$ (30)
Выразим $r_1$ и $r_2$ через $r$
$r_{1,2}^2=r^2+a^2\mp 2ra\cos\delta$ (31)
Пользуясь малостью отношения $\frac{a}{r}$, не берем во внимание его квадрат $\frac{a^2}{r^2}$ и вводя обозначение,
$\Delta=2\frac{a}{r}\cos\delta$ (32)
получаем:
$r_{1,2}^2=r^2(1\mp\Delta)$ (33)
И, следовательно:
$\frac{1}{r_{1,2}^{3}}=\frac{(1\mp\Delta)^{-3/2}}{r^{3}}$. (34)
Теперь, учитывая в свою очередь малость $\Delta$, получим:
$(1\mp\Delta)^{-3/2}=1\pm\frac{3}{2}\Delta$ (35)
Тогда
$\frac{1}{r_1^3}-\frac{1}{r_2^3}=\frac{3\Delta}{r^3}$ (36)
Подставляя (32) и (36) в (30) запишем выражение для искомой силы, разгоняющей Луну:
$F_{\tau}=-\frac{3\nu m a^2 \sin2\delta}{r^4}$ (37)
Поскольку эта сила нам задана, рассчитаем массу приливных вздутий в долях от массы всей воды мирового океана, которая оценивается величиной $1.4\cdot{21}$кг.
Угол смещения приливного вздутия за счет сноса суточным вращением Земли обозначим $\delta$, $a$ - средний радиус Земли.
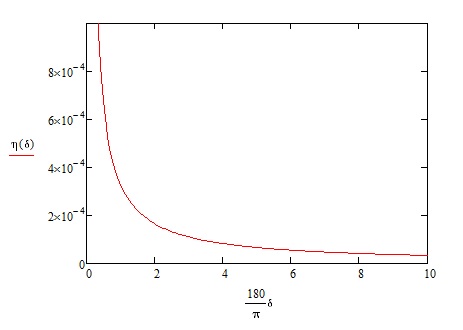 Рис. 8.
Рис. 8.
Как можно видеть на Рис. 8, доля вовлеченного в приливные вздутия вещества Земли может быть оценена как $1\cdot10^{-4}$ или чуть менее.
Теперь об энергетике процесса. Энергия Луны, как кинетическая, так и потенциальная складывается из двух частей, «земной» и «солнечной».
Так вот, полная энергия, рассчитанная относительно центра Земли ,
$E_e=\frac{1}{2} M_m (\dot{r}^2+r^2 \dot{\varphi}^2) -\frac{\mu M_m}{r}$ (38)
в среднем за год равна $-2.403\cdot10^{28}$ Дж. Энергия вращательного движения Земли равна:
$E_r=\frac{1}{2}C\omega^2$ (39)
где С – осевом момент инерции Земли, равный $8.039\cdot10^{37}$ кг м2 , а $\omega$ - угловая скорость ее суточного вращения, равная $7.292\cdot10^{-5}$ c-1.
Подставляя числовые значения в (37), получаем $E_r= 2.137\cdot10^{29} $ Дж. Этого вполне могло бы хватить, чтобы вывести Луну за сферу действия Земли, радиус которой оценивается в 925000 км [1]. Однако диссипативные процессы не позволят передать всю энергию вращения Земли Луне.
Известно, что масса приливных вздутий обратно пропорциональна кубу расстояния до возмущающего тела. Если наша оценка массы сегодняшних приливных вздутий верна, можно найти коэффициент пропорциональности. Тогда мы получим кривую характеризующую высоту приливов в прошлом и будущем (Рис. 9). По оси ординат отложена масса приливных вздутий в долях от массы мирового океана. По оси абсцисс - расстояие Земля-Луна.
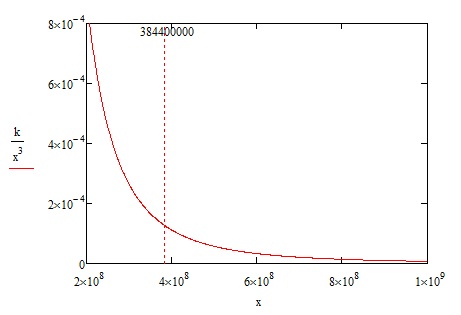 Рис. 9.
Рис. 9.
Современная эпоха характеризуется затуханием приливных процессов. Луна удаляется все медленнее. В прошлом приливы были существенно выше, а Луна удалялась быстрее.
Источники информации.
- Левантовский В. И., Механика космического полета в элементарном изложении, 3-е изд., дополненное и переработанное.— М.: Наука. Главная редакция физико-математической литературы, 1980.
- Ingus's блог
- Войдите на сайт для отправки комментариев
- 7136 просмотров


