Цели на 2014 год, связь с основной задачей Проекта
Основными целями второго этапа выполнения пректа являются:

- наполнение, созданной на первом этапе, объединенной базы данных природных факторов, медицинских и экологических показателей, а так же базы данных геопортала;

- создание дополнительных алгоритмов и программ обработки и визуализации данных различного назначения;

- создание моделей в рамках концепции рисков развития цереброваскулярной патологии;

- создание на основе геопортала системы слежения за изменением отдельных факторов состояния окружающей среды региона.

Ожидаемые в конце 2014 г. научные результаты
К концу 2014 года предполагается будут получены следующие результаты:

- в объединенной базе данных будет собрана вся доступная информация по природным факторам и медицинским показателям за 2009-2013 годы и так же частично за 2014 год;

- создан, протестирован и апробирован комплекс программ обработки данных, включающий: систему спектрального анализа данных на основе метода максимальной энтропии, систему корреляционного анализа данных, систему анализа распределений и эволюции их характеристик по скользящим рядам наблюдений:

- проведен анализ данных из, созданной базы данных для построения эмпирических моделей процессов и их взаимосвязей;

- построена модель рисков развития цереброваскулярной патологии на основе данных о флуктуации природных факторов;

- созданы тематические слои геоинформационных данных в базе данных геопортала.

1. Наполнение базы данных

В течение 2014 года продолжалось наполнение базы данных свединиями, касающимися медицинских показателей и природных факторов, включая данные о солнечной активности и геомагнитных факторах состояния магнитосферы Земли. Медицинские показатели касались данных о больных с цереброваскулярной патологией, а так же данные о парамтрах сердечной деятельности больных Ульяновской области. Это позволило существенно увеличить статистическое обеспечение вычисляющихся оценок взаимосвязи параметров и получить ряд важных характеристик взаимосвязи медицинских показателей и параметров состояния окружающей среды.

2. Создание новых алгоритмов анализа данных

2.1. Метод условной декомпозиции для ряда чисел Вольфа

Метод условной декомпозиции (МУД) был развит на предыдущем этапе работ по проекту и первые примеры его применения приведены на сайте по адресу: http://www.spacephys.ru/otchet-po-grantu-rffi-13-01-97067-rpovolzhea. На данном этапе  метод дополнялся новыми способами формирования эмпирических  признаков, с помощью которых производилось разделение гшистограмм. Важной областью применения данного метода явились данные космофизического происхождения. В первую очередь это касалось применения   МУД к задаче выяснения составляющих гистограммы распределения чисел Вольфа солнечной активности, начиная с 1749 года по настоящее время.

Работа по декомпозиции распределения эмпирического распределения ряда чисел Вольфа была проведена ранее [1] и состояла в применении метода моментов к задаче вычисления параметров (моментов) отдельных распределений смеси:
$$
         \rho(W)=(1-p(t))\rho_1(W,a_1,\sigma_1)+p(t)\rho_2(W,a_2,\sigma_2),
$$
представленной теоретически заданными распределениями $\rho_1(W,a_1,\sigma_1)$ и $\rho_2(W,a_2,\sigma_2)$. Такой подход требует проведения сложных вычислений, связанных с решением систем нелинейных алгебраических уравнений второго или третьего порядка. В силу нелинейности уравнения имеют большое число корней, для которых необходимо пороизводить отбор на физическую пригодность. Однако наибольшим недостатком такого подходя является отсутсвие прямого указания на вид признака, по которому производится разделение. Разделение производится на основе принципа близости теоретического распределения эмпирическому. В МУД все параметры вычисляются на основе вводимого заранее физического признака и не требуют сложных вычислений.

В работе [2], кроме всего прочего, исследовался ряд чисел Вольфа (рис. 1), в сопоставление с признаком превышения текущей дисперсии ряда над ее средним значением по всему ряду.

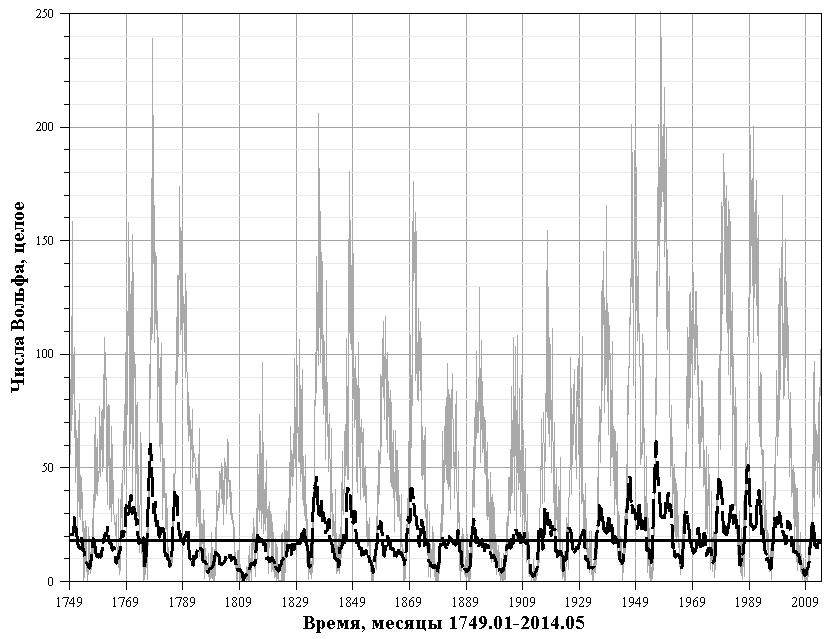
Рис. 1. Ежемесячный ряд чисел Вольфа (серая кривая), скользящая дисперсия ряда, вычисленная по интервалу 2 года (черная пунктирная кривая) и среднее значение дисперсии ряда (сплошная черная горизонтальная прямая)

На рис. 1 изображены все основные элементы данных, на основе которых производились вычисления по разделению гистограммы распределения ряда чисел Вольфа на две гистограммы, соотвествующие распределениям смеси. На рис. 2 представлена гистограмма полного ряда чисел Вольфа, представленного на рис. 1.

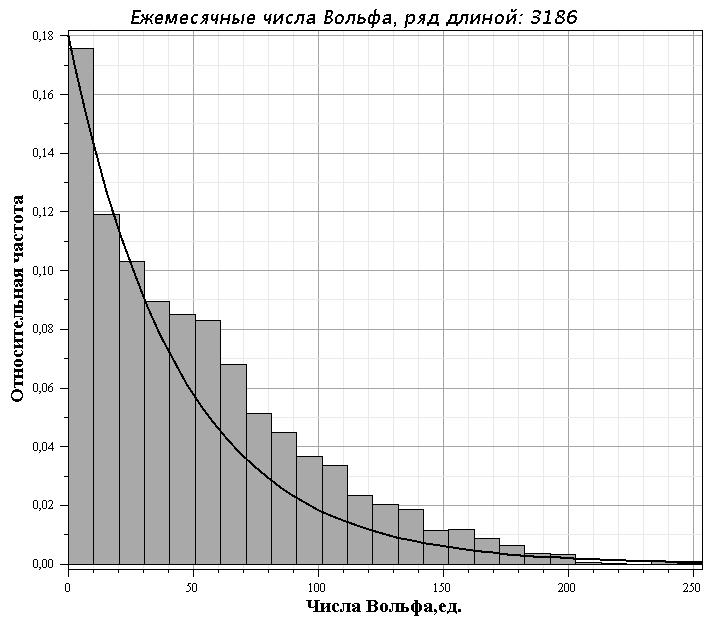
Рис. 2. Гистограмма распределения ряда чисел Вольфа (серый цвет) и теоретическое  распределение вида: $\rho_1(W,a_1,\sigma_1)=m e^{-mW}$ с $a_1=\bar{W}=1/m$ и $\sigma_1=\sqrt{M[W^2]-(\bar{W})^2}=1/m$.

Как видно из рис. 2 в целом распределение чисел Вольфа близко к распределению Больцмана, на что было обращено внимание в [1]. Это распределение можно рассматривать как распределение чисел Вольфа в равновесном состоянии Солнца (см. [1]).

Целью декомпозиции в работах [1,2] являлось выделение состояний с отклонением от равновесного. Интерпретация таких отклонений была дана в работе [1]. Поскольку неравновесный процесс сопровождается появлением сразу за период в месяц большого числа пятен на Солнце (в среднем 50-60 за месяц), то можно считать такой процесс процессом взрывного сброса энергии.  В работе [2] для выделения взрывных процессов было предложено отделять их от равновесных с помощью признака превышения текущей скользящей дисперсии среднего ее уровня по всему ряду.

Для вычисления скользящей дисперсии использовалась стандратная формула несмещенной оценки дисперсии на отрезке времени длиной $2P+1$ отсчетов с совмещением времени получения такой оценки в середине отрезка. Т.е. величина скользящей дисперсии к моменту времени с номером $k$ вычислялась по формуле:
$$
         \sigma^2_k=\frac{1}{2P}\sum\limits_{i=-P}^P\Big(W_{k+i}-\overline{W}_k\Big)^2,~k=P,\ldots,N-P,
$$
где $N$ - общая длина ряда, а скользящее среднее $\overline{W}_k$ вычислялось по аналогичной формуле:
$$
\overline{W}_k=\frac{1}{2P+1}\sum\limits_{i=-P}^PW_{k+i},~k=P,\ldots,N-P,
$$

Принцип разделения гистограмм состоял в проверке условиий: I) $\sigma^2_k < \overline{\sigma^2}$ или II) $\sigma^2_k \ge \overline{\sigma^2}$. Здесь:
$$
    \overline{\sigma^2}=\frac{1}{N-2P-1}\sum\limits_{k=1}^{N-2P-1}\sigma^2_k.
$$
При выполнении условия I считается, что реализуется состояние равновесия и соотвествующее значение числа Вольфа относится к гистограмме равновесного распределений. При выполнении условия II считается, что реализуется состояние "взрыва", и соответствующее значение числа Вольфа относится к распределению возмущеных состояний.

В процессе обработки проверялись несколько ваотантов значений числа $P$. Оказалось, что в широком диапазоне значений $P$, соотвествующих длительности интервала усреднения от 1 до 3 лет результаты не сильно отличаются друг от друга. Поэтому для оканчального варианта обработки был выбран интервал 2 года. Обработки представлены на рис. 3 и 4.

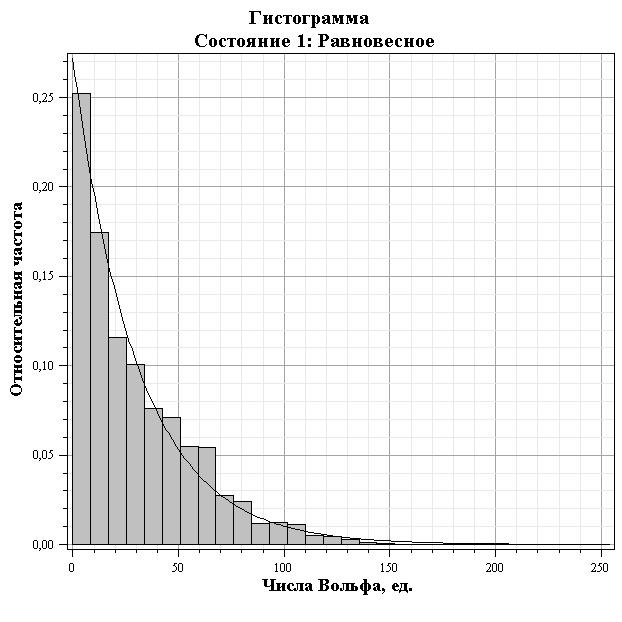
Рис. 3. Гистограмма значений чисел Вольфа в условно равновесных состояних. Сплощная кривая - теоретическое распределение Больцмана со средним значением, равным среднему по гистограмме.

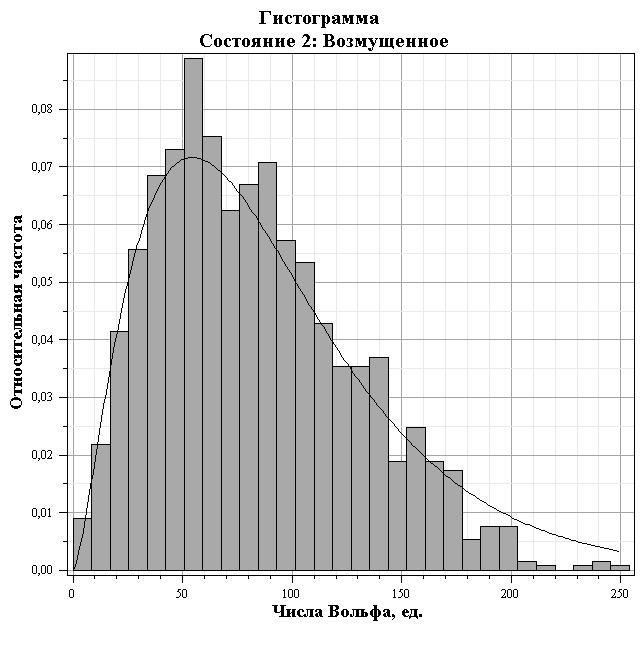
Рис. 4. Гистограмма значений чисел Вольфа в условно  состояних "взрыва". Сплощная кривая - теоретическое распределение вида: $\rho_2(w)=\frac{4}{3\sqrt{\pi}s_2^{5/2}}w^{3/2}e^{-w/s_2}$.

Распределение $\rho_2(w)=\frac{4}{3\sqrt{\pi}s_2^{5/2}}w^{3/2}e^{-w/s_2}$ является наилучшей с точки зрения критерия $\chi^2$. Для сравнения на рис. 5 приведы аналогичные гистограммы из работы [1].

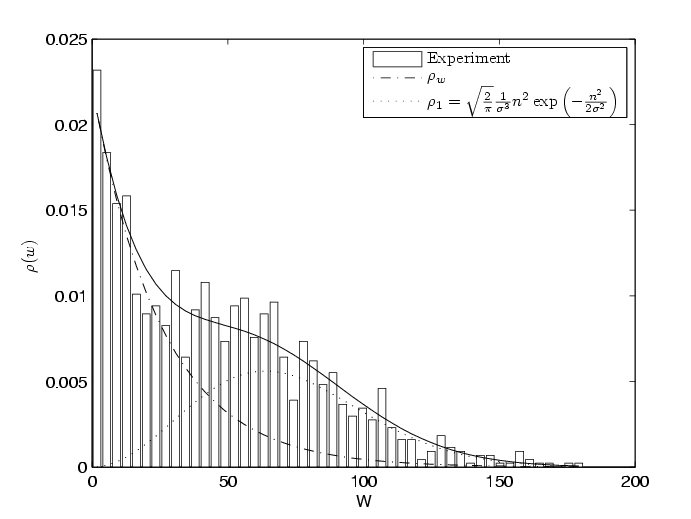
Рис. 5. Гистограмма и теоретические распределения смеси, полученные в работе [1] с помощью метода моментов. Пунктиром обозначено равновесное распределение, а сплошной кривой - смесь теоретических распределений.

Из сравнения графиков на рис. 3,4,5 видно, что результат обработки с помощью метода условной декомпозиции по форме совпадает с результатами метода моментов, но представлет разбиение на конкретно сформулированном критерии в форме условия превышения дисперсии.

Метод декомпозиции можно применять и к задаче исследования скользящих рядов. По аналогии с работой [1] в работе [2] был проведенн аналогичный анализ скользящих рядов. Длина скользящих рядов как и в работе [1] выбиралась равной  100 годам или 1200 точек. На рис. 6, 7, 8 представлены результаты такой обработки в форме эволюции параметров распределений смеси и вероятности разделения $p(t)$.

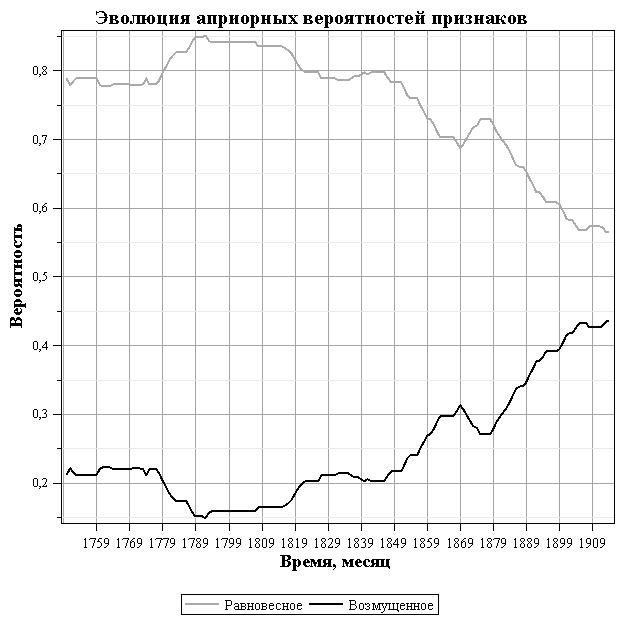
Рис. 6. Эволюция  вероятности разденления $p(t)$ в смеси из работы [2] для скользящих рядов наблюдения длиной 100 лет с шагом 2 года. Черная сплошная кривая $p(t)$, серая - $1-p(t)$.

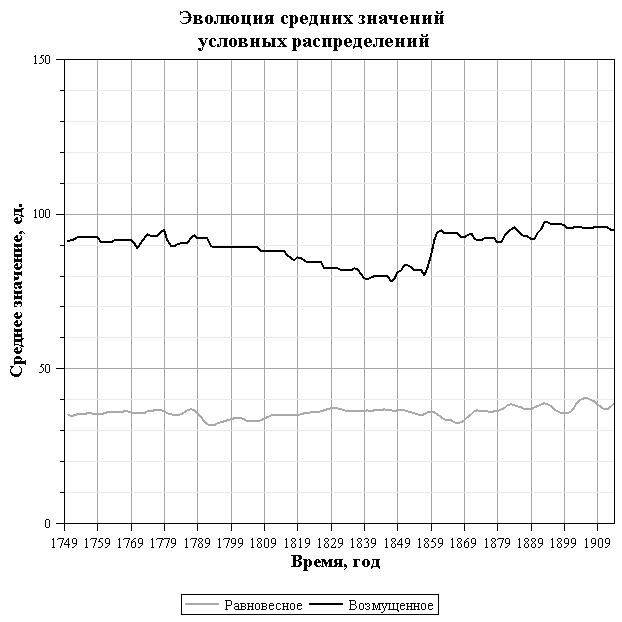
Рис. 7. Эволюция   средних значений гистограмм в смеси из работы [2] для скользящих рядов наблюдения длиной 100 лет с шагом 2 года. Черная сплошная кривая - среднее значение чисел Вольфа возбужденных состояний , серая - равновесных.

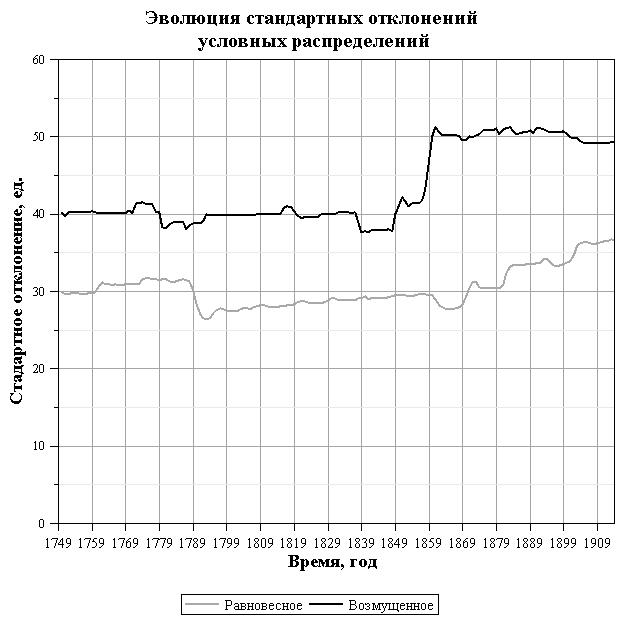
Рис. 8. Эволюция   стандартных отклонений гистограмм в смеси из работы [2] для скользящих рядов наблюдения длиной 100 лет с шагом 2 года. Черная сплошная кривая - стандартное отклонение  чисел Вольфа возбужденных состояний , серая - равновесных.

Для сравнения приводим графики из работы [1], организованных несколько иначе, чем на предыдущих графиках.

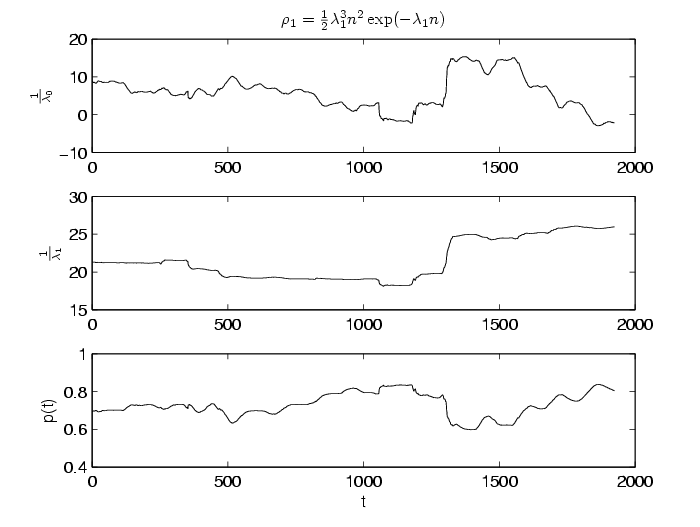
Рис. 9. Эволюция   средних значений, стандартных отклонений и вероятности $1-p(t)$  теоретического распределения Больцмана в смеси из работы [1] для скользящих рядов наблюдения длиной 100 лет с шагом 2 года.

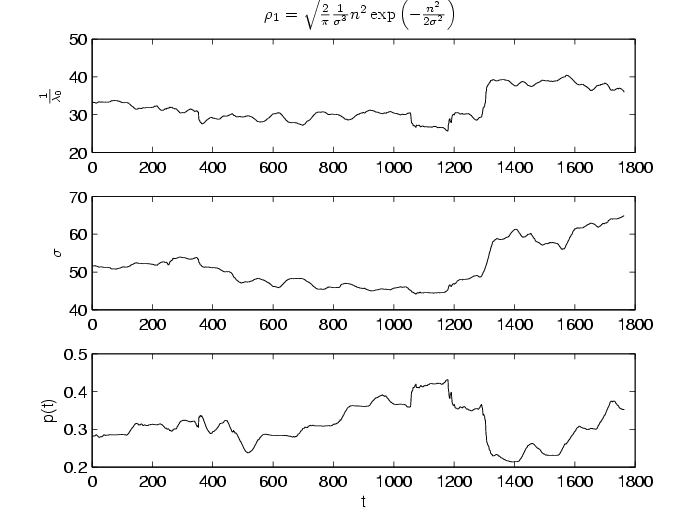
Рис. 10. Эволюция   средних значений, стандартных отклонений и вероятности $p(t)$  теоретического распределения типа Максвелла в смеси из работы [1] для скользящих рядов наблюдения длиной 100 лет с шагом 2 года.

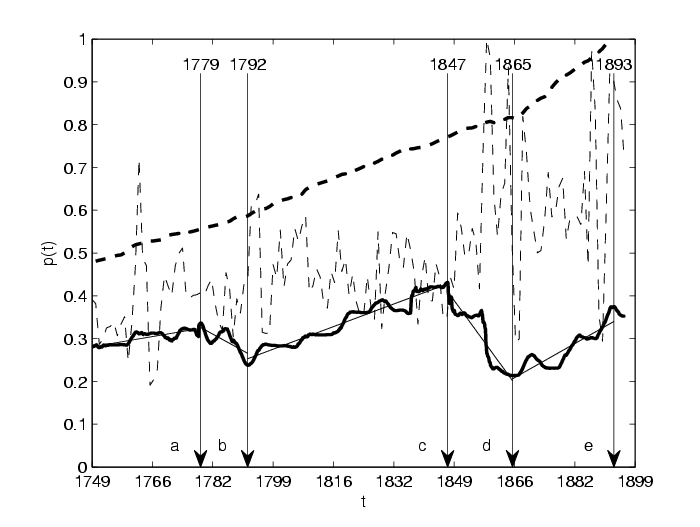
Рис. 11. Эволюция   вероятности $p(t)$  возбужденных состояний из работы [1] для скользящих рядов наблюдения длиной 100 лет с шагом 2 года. Пунктиром показаны значения колическтва нитратов в льдах Гренландии и их скользящих средних за  100 лет. Вертикальные линии указывают  на моменты серьезных изменений в состоянии Солнца (см. [1]).

Как видно из сравнения графиков работ [1] и [2] они описывают одну и ту же эволюцию параметров распределений смеси, что указывает на пригодность использования метода условной декомпозиции для анализа рядов наблюдений при том, что объем вычислений оказщывается значительно меньшим, а для интерпретации результатов имеются дополнительные возможности, связанные с конкретной формулировкой признаков разделений гистограмм.

[1]  В.М. Журавлев, С.В. Летуновский. Анализ долговременной эволюции активности Солнца на основе ряда чисел Вольфа. (I Методика).  // Известия высших учебных заведений. Поволжский регион. Физико-математические науки, 2010, N4, c. 120-129 (zip-архив)
В.М. Журавлев, С.В. Летуновский. Анализ долговременной эволюции активности Солнца на основе ряда чисел Вольфа. (II Результаты).  // Известия высших учебных заведений. Поволжский регион. Физико-математические науки,.-2011.-N3.-C. 164-174 (zip-архив)

[2]  В.М. Журавлев, В.Н. Морозов, М.С. Петряков, В.В. Самойлов. Метод условной декомпозиции эмпирических распределений и его применение к задаче анализа рядов наблюдений. Известия высших учебных заведений. Поволжский регион. Физико-математические науки. Издательство: Пензенский государственный университет - 2014- №3-С. 178-197

2.2. Алгоритмы визуализации спутниковых данных с привязкой к географической карте

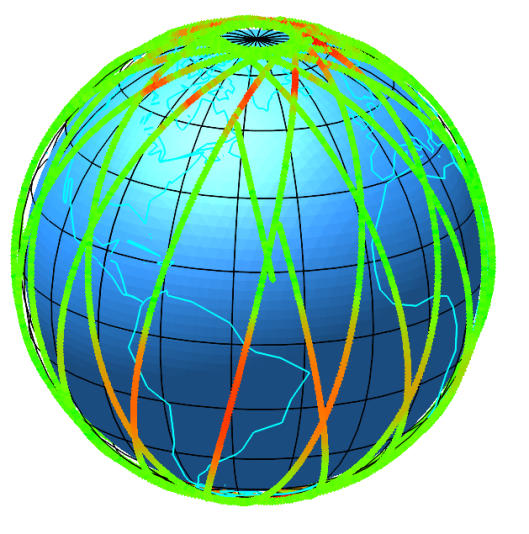
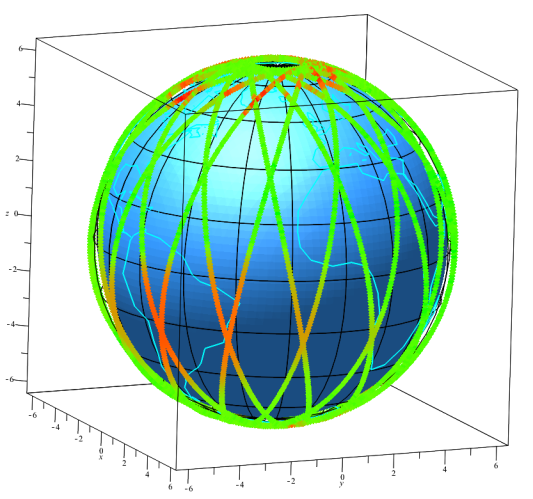
Для анализа спутниковых данных очень часто необходимо иметь средства их визуализации непосредственно к географической карте в 2D формате или 3D формате. Для этого в рамках проекта был создан ряд алгоритмов и программ, написанных в языке символьных вычислений Maple. Алгоритмы позволяют данные, получаемые на орбитальных спутниках и представленные в виде текстовых файлов, изображать в виде 2D и 3D  орбит спутников, цвет точек которых отражает измеренные значения параметров космической среды. В каечестве  примера приведем изображения величины потока электронов, полученных спутником metop-2.

Рис. 12. Данные о потоках электронов $E>30$ кЭв, $E>100$ кЭв, и широта положения спутника.

a. Спутник metop-2

b. Спутник noaa-15

Рис. 13. Данные о потоках электронов $E>30$ представленные в форме 3D-карты.

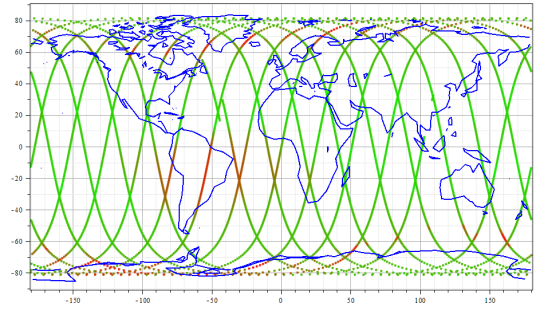
a. Спутник metop-2

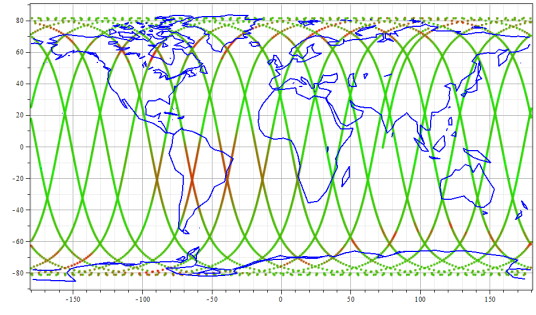
b. Спутник noaa-15

Рис. 14. Данне о поках электронов $E>30$ кЭв, предситавленные в форме 2D-карты.

2.3. Алгоритмы вычисления собственных чисел и векторов симметричных матриц большой размерности