II. Опрокидывающиеся электромагнитные и акустические волны в сильнонелинейных системах
Введение.
Волны в нелинейных средах без дисперсии описываются, как правило, квазилинейными уравнениями первого порядка. Уравнения такого типа характерны для задач гидродинамики газа, жидкости и плазмы. Однако для таких разделов физики как теория электромагнитных волн в нелинейных средах их описание строится на основе уравнений Максвелла, которые являются гиперболическими уравнениями второго порядка. В связи с этим возникает вопрос о существовании связи между процессами, которые описываются квазилинейными гиперболическими уравнениями первого и второго порядка. Характерным явлением, которое наблюдается в системах первого типа (квазилинейные гиперболические уравнения первого порядка) - это опрокидывание фронта волны и образование ударных волн. В [1] было впервые показано, что в электромагнитных системах при определенных условиях могут возникать явления опрокидывания волн. Возможность существования такого же явления в нелинейной керровской среде было показано в работе [2]. В работе [3] была найдена общая связь между большим классом нелинейных многомерных волновых уравнений с квазилинейными уравнениями первого порядка. Эта общая связь дает возможность исследовать некоторые нелинейные эффекты, которые могут возникать при распространении электромагнитных волн в диэлектриках и акустических волн в сжимаемой среде. В настоящей работе исследуются некоторые следствия развитой в [3] теории опрокидывания волн к некоторым задачам оптики и акустики.
2 Волны в нелинейной среде без дисперсии
Опираясь на [3] опишем некоторые основные положения развитой там теории. Связь между квазилинейными уравнениями первого порядка и нелинейными гиперболическими уравнениями второго порядка, описывающих распространение нелинейных электромагнитных волн в среде с нелинейной поляризацией можно проследить и для многомерных систем. Для этого рассмотрим систему квазилинейных уравнений следующего вида:
$$\frac{\partial E}{\partial x_{\alpha}} = A_{\alpha}(E)E_t,~~~\alpha=1,\ldots,n,\tag{2.1}\label{EqQLn}$$ где ${\bf A}(E)=\Big(A_{1}(E),\ldots,A_n(E)\Big)$ - вектор-функция, зависящая от неизвестной функции $E=E({\bf x},t)$, ${\bf x}=(x_1,\ldots,x_n)$ и $t$. Решением этой системы является функция $E=E({\bf x},t)$, удовлетворяющая алгебраическому уравнению: :
$$H\Big(E,t+A_1(E)x_1+\cdots+A_n(E)x_n\Big)=0,\tag{2.2}\label{SolH}$$
где $H(\xi,\eta)$ - произвольная дифференцируемая функция двух аргументов $\xi=E$ и $\eta=t+({\bf A},{\bf x})$, где $\Big({\bf A}(E),{\bf x}\Big)=A_1(E)x_1+\cdots+A_n(E)x_n$. Это устанавливается последовательным дифференцированием (2) по переменным $x_1,\ldots,x_n,t$:
$$E_{,\alpha}H_{\xi} + \Big(A_{\alpha}+({\bf A}'(E),{\bf x})E_{,\alpha}\Big)H_{\eta}=0,~~~\alpha=1,\ldots,n;$$
$$E_{,t}H_{\xi} +\Big(1+({\bf A}'(E),{\bf x})E_{t}\Big)H_{\eta}=0. \tag{2.3}\label{EqDiffH}$$ Условием совместности этих уравнений является система уравнений (1).
Из системы уравнений (1) прямым дифференцированием находим важное следствие: $$\Delta E = \frac{\partial}{\partial t}\left(|{\bf A}|^2E_t\right),\tag{2.4}\label{EqE}$$ где $$|{\bf A}(E)|^2=\sum\limits_{\alpha=1}^n A^2_{\alpha}(E).$$ Введем обозначение::$$\diamondsuit_{|{\bf A}|} = \Delta-\frac{\partial}{\partial t}\left(|{\bf A}(E)|^2\frac{\partial}{\partial t}\right),$$ так что уравнение (\ref{EqE}) можно записать в следующем виде:$$\diamondsuit_{|{\bf A}|} E =0.$$
Важным свойством уравнения (4) , вне зависимости от его интерпретации и типа нелинейности, является инвариантность его формы относительно преобразований вращений вектор-функции ${\bf A}(E)$ в координатном пространстве $R^{n}$. Все такие преобразования оставляют инвариантной длину вектора ${\bf A}(E)$ в $R^{n}$. Введем обозначение: $R(E)=|{\bf A}(E)|=\sqrt{A_1^2(E)+\cdots+A_n^2(E)}$. Тогда вектор функцию ${\bf A}(E)$ можно представить в следующем общем виде: $${\bf A}=R(E){\bf n}(E),\tag{2.5}\label{DefA}$$ где ${\bf n}(E)$ - произвольный единичный вектор, зависящий от значения функции $E$. Вектор-функция ${\bf n}(E)$ может быть связана с точкой на единичной сфере размерности $n-1$, угловые координаты которой зависят от $E$ произвольным образом. Инвариантность формы уравнения (\ref{EqE}) относительно выбора функциональной зависимости единичного вектора ${\bf n}(E)$ от $E$ означает, что решение (2) при любом выборе $H(\xi,\eta)$ и ${\bf n}(E)$ является решением уравнения (\ref{EqE}) . При этом следует отметить, что произвольный выбор функции $H(\xi,\eta)$ в силу (\ref{SolH}) допускает в решениях системы (\ref{EqQLn}) произвол, ограниченный функцией лишь одного аргумента.
${\bf Утверждение\ 1}$. Каждое решение системы квазилинейных уравнений (\ref{EqQLn}) для заданной функции $R(E)=|{\bf A}(E)|$ и произвольной вектор функции ${\bf n}(E):~|{\bf n}|^2=1$ является решением уравнения (\ref{EqE}) . Обратное утверждение неверно.
${\bf Утверждение\ 2}$. Каждое решение системы квазилинейных уравнений (\ref{EqQLn}) для заданной функции $R(E)=|{\bf A}(E)|$ и произвольной вектор-функции ${\bf n}(E):~|{\bf n}|^2=1$ является решением уравнения эйконала:
$$\sum\limits_{\alpha=1}^n \Big(E_{,\alpha}\Big)^2 = |{\bf A}(E)|^2\Big(E_t\Big)^2.$$
Это утверждение является прямым следствием системы (\ref{EqQLn}) .
Еще одно следствие можно получить из (\ref{EqQLn}) с помощью дифференцирования его по и комбинирования с самой этой системой уравнений. Оно имеет вид уравнения Эйлера.
${\bf Утверждение\ 3}$. Вектор-функция ${\bf U}=\{U^1,\ldots,U^n\}$ с компонентами:
$$U^{\alpha} = -\frac{1}{|{\bf A}|^2}A^{\alpha}(E),~~\alpha=1,\ldots,n,$$
и функция $\rho = |{\bf A}|^2E_t$ удовлетворяют системе однородных уравнений Эйлера:
$$\begin{eqnarray*} && \frac{\partial U^{\alpha}}{\partial t}+U^{\beta}\frac{\partial U^{\alpha}}{\partial x^{\beta}}=0,\quad\alpha=1,\ldots,n;\tag{2.6a}\label{EqEuler}\\ && \frac{\partial \rho}{\partial t}+\frac{\partial }{\partial x^{\alpha}}\Big(\rho U^{\alpha}\Big)=0\end{eqnarray*}$$
для потока идеальной жидкости со скоростью ${\bf U}$ и плотностью $\rho$ .
Справедливость первого уравнения устанавливается прямым дифференцированием вектор-функции ${\bf U}$
и последующим использованием исходной системы уравнений (\ref{EqQLn}) . Второе уравнение эквивалентно уравнению (\ref{EqE}) при использовании определения для функции $\rho$ и ${\bf U}$.
2.3 Физическая интерпретация уравнений
Уравнение (4) , как и в одномерном случае, преобразуется к уравнению плоскополяризованных электромагнитных волн в среде с нелинейной поляризацией $P(E)$, связанной с вектор-функцией ${\bf A}$ соотношением: $$P'(E) = \frac{c^2}{4\pi}|{\bf A}(E)|^2-1.$$ В этом случае уравнение (4) имеет точный вид уравнения Максвелла для электромагнитных волн в среде с нелинейной поляризацией $P(E)$: $$ c^2\Delta E - E_{tt} = 4\pi\frac{\partial^2}{\partial t^2}P(E),\tag{2.6b}\label{EqMaxP}$$ и соответствует отсутствию дисперсии в среде. Это определяет специфические условия его применения в электродинамике. В частности такие условия описаны в [1] и [2].
Другая физическая интерпретация уравнения (6) соответствует звуковым волнам в идеальном газе. Уравнения акустических волн в такой среде имеют вид: $$\frac{\partial}{\partial t}\rho u^{\alpha} + \frac{\partial}{\partial x^{\beta}}\rho u^{\alpha} u^{\beta} = -\frac{\partial P}{\partial x^{\alpha}},$$
$$\frac{\partial}{\partial t}\rho + \frac{\partial}{\partial x^{\beta}}\rho u^{\beta}=0.$$ Первое векторное уравнение этой системы - уравнение Эйлера для скорости потока $u^{\alpha}$ , а последнее - уравнение неразрывности. Для адиабатических звуковых волн в газе давление $P$ является заданной функцией плотности газа $\rho$. Вычисляя дивергенцию от первого векторного уравнения этой системы, приходим к уравнению для $\rho$: $$\rho_{tt} = \Delta P(\rho) + \frac{\partial^2}{\partial x^{\alpha} \partial x^{\alpha}}\Big(\rho u^{\alpha} u^{\beta}\Big).$$ Пренебрегая последним слагаемым в правой части (инерционной нелинейностью) и переходя к одномерному случаю, получаем уравнение для давления в среде в форме: $$P_{xx}=\frac{\partial^2}{\partial t^2}\rho(P).\tag{2.7}\label{EqAcustP3D}$$ В рассматриваемом одномерном случае: $$\rho'(P) = \frac{c^2}{V^2(E)}.$$
2.4 Точные решения квазилинейных уравнений первого прядка
Решения уравнения (4) , совпадающие с решениями системы квазилинейных уравнений (1) , обладают особыми свойствами, которые выделяют их из всех других типов возможных решений этого уравнения. Поскольку векторное поле ${\bf A}={\bf A}(E({\bf x},t))$ в заданный момент времени $t$ зависит только от значения функции $E$, то оно постоянно на изоповерхностях функции $E$: $\left.{\bf A}\right|_{E={\rm const}}={\rm const}$ . Однако согласно самим уравнениям (1) поле ${\bf A}$ коллинеарно в каждой точке пространства полю $\nabla E$ , которое всюду ортогонально гиперповерхности $E=E_{0}(t)$. Отсюда следует, что изоповерхностями функции $E$ являются гиперплоскости, поскольку в любой точке этой гиперповерхности нормаль к ней имеет одно и тоже направление, зависящее только от $E$ . Поскольку, как уже отмечалось выше, форма уравнения (4) не зависит от направления поля ${\bf A}$ в каждой точке, то каждое решение (1) , совпадающее с одним из решений (4) при заданной функции $R(E)=|{\bf A}|$ , будет определяться вектор-функцией ${\bf n}(E)$. Точнее это можно выразить в форме следующего утверждения:
${\bf Утверждение\ 4}$. Решение системы (1) $E({\bf x},t)$ при заданной функции $R(E)=|{\bf A}|$ определяется однозначно парой функциональных параметров $\{{\cal C}_n,E(s,t)\}$, в которой ${\cal C}_n$ является независящей от времени однопараметрической кривой, называемой далее базовой:
$$\frac{dx^{\alpha}}{ds} = n^{\alpha}(s),~~~A^{\alpha}(E(s))=R(s)n^{\alpha}(s),\tag{2.9}\label{EqCurn}$$
в координатном пространстве ${\cal R}^n$ , и функцией $E(s,t)=E({\bf x}(s),t)$ - являющейся решением уравнения Хопфа: $$\frac{\partial E}{\partial s} = R(E)\frac{\partial E}{\partial t}.\tag{2.10}\label{EqHopf}$$
${\bf Доказательство}$. Поскольку выше было доказано, что изоповерхностями функции $E({\bf x},t)$ являются гиперплоскости, к которым ортогональны поля ${\bf A}=R{\bf n}$ и ${\bf n}$, то первую часть утверждения можно считать доказанной. Пусть ${\cal C}_n$
- кривая, заданная уравнением (\ref{EqCurn}) . Тогда, используя систему уравнений (1) , имеем:
$$\frac{\partial E}{\partial s} = \sum\limits_{\alpha=1}^n\frac{\partial E}{\partial x^\alpha}\frac{\partial x^{\alpha}}{\partial s}= \sum\limits_{\alpha=1}^n R(E)E_t n^{\alpha}(E(s,t))n^{\alpha}(E(s,t))=R(E)E_t.\tag{2.11}\label{EqHopf1}$$
Последнее равенство следует из условия $|{\bf n}|^2=\sum\limits_{\alpha=1}^n n^{\alpha}n^{\alpha}=1$ . Отсюда сразу следует (10) . Заметим, что решение $E(s,t)$ уравнения Хопфа находится как решение уравнения:
$$H(E,t+R(E)s)=0,\tag{12}\label{SolHopf}$$
где $H(\xi,\eta)$ та же функция, что и в решении (\ref{SolH}) , что соответствует выбору параметра $s$ по формуле:
$$\sum\limits_{\alpha=1}^n n^{\alpha}(E(s,t))x^{\alpha}(s)=s.$$
В результате решение (\ref{SolH}) переходит в решение (\ref{SolHopf}) .
Такие решения в дальнейшем будем называть ${\bf ривертонами}$ (``river'' - река). Как следует из приведённого утверждения, ривертоны представляют собой бегущие плоские волны, направление распространения которых в каждой точке пространства не меняется со временем и определяется касательной к кривой ${\cal C}_n$ . Значение же функции на каждой гиперплоскости меняется со временем и представляет волну с опрокидывающимся фронтом. Кривая ${\cal C}_n$ фактически представляет собой проекцию характеристики ривертона на вещественное координатное пространство ${\cal R}^n$ . Сама же характеристика является траекторией фронта волны в пространстве-времени ${\cal R}^n\times T$ , где $T$ - ось времени.
Заметим, что для $n=1$ кривая ${\cal C}_n$ совпадает с одномерной осью $x^1$, а уравнение (1) переходит в уравнение Хопфа (10) .
В случае, если кривая ${\cal C}_n$ не является прямой, то гиперплоскости, ортогональные кривой ${\cal C}_n$, будут пересекаться по некоторым гиперплоскостям. Совокупность всех точек пересечения гиперплоскостей, ортогональных ${\cal C}_n$, заполняет в общем случае некоторую область ${\cal V}^n\subset{\cal R}^n$ , которая целиком определяется геометрией кривой ${\cal C}_n$ . В общем случае в области ${\cal V}^n$ лежат точки, на которых пересекаются гиперплоскости $s={\rm const}$ бесконечное число раз. На границе этой области число пересечений конечно. Поэтому в ${\cal V}^n$ непрерывные решения отсутствуют. В некотором смысле границы областей ${\cal V}^n$ подобны каустикам в оптике, но определяются с геометрической точки зрения иначе.
Отметим так же то обстоятельство, что ривертоны по сути являются решениями задачи Коши для уравнений (1) и (4) . Этот момент важен, поскольку в Утверждении 4 кривая ${\cal C}_n$ задается в начальный момент времени вместе с начальным распределением функции $E_0=E(s,Å_0)$ вдоль этой кривой. Это означает, что вместе с геометрическими характеристиками кривой ${\cal C}_n$ задаются пространственные свойства ривертона, которые определяются геометрией областей однозначности функции $E({\bf x},t)$.
2.5 Общая структура ривертонов
Пусть задана некоторая базовая кривая ривертона в форме системы уравнений (9) . Интегрируя эту систему приходим к параметрическому заданию данной кривой в форме уравнений:
$$x^{\alpha}=X^{\alpha}(s) = \int n^{\alpha}(s)ds + x^{\alpha}_0.$$
Постоянные $x^{\alpha}_0$ указывают положение кривой относительно начала координат. В этом случае гиперплоскости уровня $E={\rm const}$ в ${\cal R}^n$ , соответствующие заданному значению параметра $s$, можно записать в виде уравнения:$$\sum\limits_{\alpha=1}^n x^{\alpha}n^{\alpha}(s)= \sum\limits_{\alpha=1}^n X^{\alpha}(s)n^{\alpha}(s)=\frac{1}{2}\frac{d}{ds}\sum\limits_{\alpha=1}^n \Big[X^{\alpha}(s)\Big]^2.$$ Две гиперплоскости, отвечающие двум значениям $s_1$ и $s_2$ параметра $s$ пересекаются в пространстве ${\cal R}^n$ по совокупности точек, являющихся решением двух таких уравнений: $$\sum\limits_{\alpha=1}^n x^{\alpha}n^{\alpha}(s_1)= F(s_1),\quad \sum\limits_{\alpha=1}^n x^{\alpha}n^{\alpha}(s_2)= F(s_2),\tag{2.13}\label{EqP12}$$ где $$F(s)=\frac{1}{2}\frac{d}{ds}\sum\limits_{\alpha=1}^n \Big[X^{\alpha}(s)\Big]^2.$$ Эти совокупности точек образуют в ${\cal R}^n$
гиперплоскости размерности $n-2$.
Огибающая множества всех таких гиперплоскостей будет образовывать границу областей однозначности и многозначности ривертона.
Огибающую области многозначности без ограничения общности можно вычислить следующим образом. Огибающая состоит из точек пересечения всех бесконечно близких гиперплоскостей при $s_1\to s_2$. Систему (13) можно разрешить относительно первых двух координат $x_1$ и $x_2$, в результате чего они становятся функциями $s_1$ и $s_2$, а так же остальных координат $x_{3},\ldots,x_{n}$:$$\begin{eqnarray*}&& x_1(s_1,s_2) = \frac{G(s_2,{\bf x})n^2(s_1)-G(s_1,{\bf x})n^2(s_2)}{n^2(s_1)n^1(s_2)-n^2(s_2)n^1(s_1)},\tag{1.14}\label{EqExE}\\ \nonumber && x_2(s_1,s_2) = -\frac{G(s_2,{\bf x})n^1(s_1)-G(s_1,{\bf x})n^1(s_2)}{n^2(s_1)n^1(s_2)-n^2(s_2)n^1(s_1)}.\end{eqnarray*}$$ Здесь $$G(s,{\bf x})=F(s)-\sum\limits_{\alpha=3}^n x^{\alpha}n^{\alpha}(s).$$ В пределе $s_1\to s_2\to s$ мы получаем уравнение гиперплоскости ${\cal E}^{n-2}(s_1,s_2)$ размерности $n-2$, являющейся пересечением двух бесконечно близких гиперплоскостей $E=E(s_1)$ и $E=E(s_2)$. В пределе $s_1\to s_2\to s_0$ получаем множество ${\cal E}^{n-2}(s_0)$ гирперплоскостей, зависящих от параметра $s_0$, образующих гиперповерхность ${\cal G}^{n-1}$, к которой касательны все гиперплоскости $E=E(s_0)$ для значений параметра $s_0$ в некотором интервале $(s_1,s_2)$. Поскольку все гиперплоскости $E=E(s)$ из интервала $s\in (s_1,s_2)$ касательны к ${\cal G}^{n-1}$ , то они пересекаются друг с другом в области, лежащей в ${\cal R}^{n}$ с одной стороны по отношению к ${\cal G}^{n-1}$ . Следовательно, гиперповерхность ${\cal G}^{n-1}$ разделяет области многозначности и однозначности ривертона, по крайней мере, для интервала $(s_1,s_2)$ параметра $s$.
Переходя к пределу $s_1\to s_2\to s$ в соотношениях (\ref{EqExE}) , получаем уравнения параметрического задания гиперповерхностей ${\cal G}^{n-1}$ : $$x_1(s) = \frac{G'_1(s,{\bf x})}{N'_1(s)},\quad x_2(s)=\frac{G'_2(s,{\bf x})}{N'_2(s)},\tag{2.15}\label{EqX1}$$
где $$\begin{eqnarray*}&& G'_1(s,{\bf x}) = \frac{d}{ds}\left(\frac{G(s,{\bf x})}{n^1(s)}\right),~~G'_2(s,{\bf x}) = \frac{d}{ds}\left(\frac{G(s,{\bf x})}{n^2(s)}\right),\\ && N'_1(s) = \frac{d}{ds}\left(\frac{n^1(s)}{n^2(s)}\right),~~N'_2(s) = \frac{d}{ds}\left(\frac{n^2(s)}{n^1(s)}\right).\end{eqnarray*}$$
На рис. 1. и 2 приведены примеры вычисления областей однозначности ривертонов для размерности координатного пространства $n=2$ в случае кривых: $y=x^2$ (рис.1) и $y=\sin(x)$
(рис. 2). На рисунках сплошными прямыми обозначены линии уровня $E=const$.
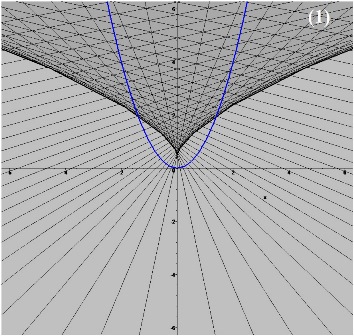
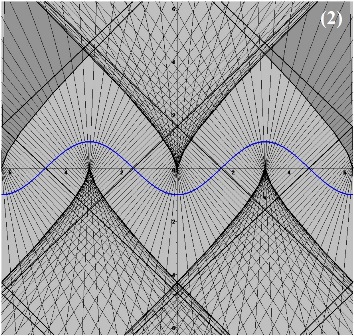 Границы областей многозначности (на рисунках обозначены жирной кривой) и задаются параметрически следующими соотношениями:
Границы областей многозначности (на рисунках обозначены жирной кривой) и задаются параметрически следующими соотношениями:
$$\begin{eqnarray*}&& (1):~~ X(s) = -4s^3,~~ Y(s) = (1+6s^3)/2;\\&& (2):~~ X(s) = s-2{\rm tg}(s)+\sin(2s)/2,~~ Y(s) = \Big(1-\cos(2s)\Big)/\cos(s).\end{eqnarray*}$$
В качестве еще одного примера приведеи график областей многозначности для части эллипса: $y=b\sqrt{1-x^2/a^2}$ c $a=5.2,b=4$ в верхней полуплоскости.
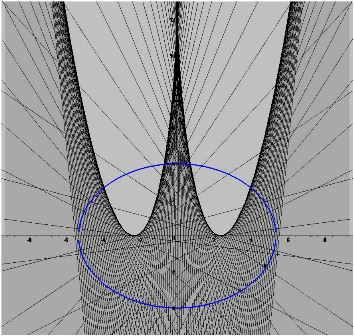

Для нижней части эллипса будет аналогичная картина областей. Однако для замкнутой кривой областей однозначности не остается. Можно добится определенной однозначности решений при наложении в этом случае периодических условий на начальное распределение решения.
На последнем рисунке приведено графическое изображение поверхностей уровня и границ многозначности для ривертона с базовой кривой $y=x^2-x^4$. Функция $F(s)$ имеет в этом случае вид: $$F(s)=s+2s^3(1-2s^2)(1-s^2).$$ Парамтрическое уравнение границы многозначности в этом случае будет иметь такой вид: $x=-8\frac{(3s^2-6s^4+4s^6-1)s^3}{6s^2-1},\quad y=-\frac{1+6s^2-30s^4+28s^6}{2(6s^2-1)}.$
Данные примеры демонстрируют важные общие особенности структуры ривертонов. Области многозначности ривертонов образуются с той стороны от базовой кривой, с которой находится центр касательной окружности, имеющий радиус, равный радиусу крнивизны. Величина радиуса кривизны определяет характериное рассточние от базовой кривой до границы области многозначности.
Появление термина "ривертон" иллюстрирует рисунок 5, на котром изображены линии тока, соотвествующие гидродинамическому потоку (\ref{EqEuler}) .
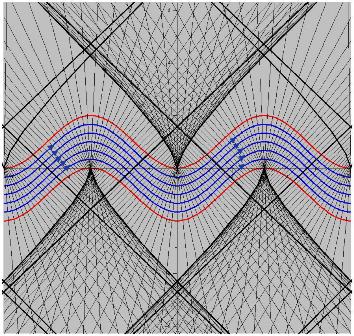
Рис. 5. Линии тока, соотвествующие гидродинамической интерпретации ривертона.
Рассматривая общие свойства огибающих, которые задаются уравнениями (15) , легко понять, что в случае замкнутых кривых или кривых с самопересечениями области однозначности решений в форме ривертона отсутствуют. Однако в этом случае, дополняя решением некоторыми условиями периодичности, можно, по крайней мере, для некоторых кривых, например, окружностей, построить однозначные решения. Мы не будем доказывать этот факт специально, поскольку для окружностей он практически очевиден, а для более общего случая требует более детального анализа, что выходит за рамки данной работы.
2.6 Опрокидывание фронта
Области неоднозначности ${\cal V}^n$ - не единственная особенность ривертонов. Некоторые изоповерхности функции $E({\bf x},t)$ в ${\cal V}^n$ являются целиком поверхностями опрокидывания фронта волны в соответствии со свойствами уравнения Хопфа (\ref{EqHopf}). Все точки пространства, в которых происходит ветвление решения или опрокидывание его фронта, определяются из условия обращения производных решения по координатам в бесконечность. По аналогии с этим мы можем найти значения параметра $s$ , в которых происходит опрокидывание фронта ривертонов. Из (\ref{EqDiffH}) имеем: $$E_{,\alpha}=-\frac{A_{\alpha}H_{\eta}}{H_{\xi}+({\bf A}',{\bf x})H_{\eta}}.$$ Отсюда находим общее уравнение для поверхности опрокидывания фронта: $$H_{\xi}+({\bf A}',{\bf x})H_{\eta} = 0,\quad H(\xi,\eta)=0.\tag{2.16}\label{EqFront}$$ В области однозначности поверхность опрокидывания фронта представляет собой некоторую гиперплоскость $E=E(s_{*})$ со значением параметра $s=s_{*}$, которое находится из аналогичного соотношения для уравнения Хопфа (\ref{EqHopf}): $$s_{*}=-\frac{H_{\xi}}{R'(E(s_{*},t_{*}))}.$$
Для полноты анализа укажем на следующее свойство ривертонов:
${\bf Утверждение\ 5}$. Пусть $E({\bf x},t)$ - решение (1) в виде ривертона. Тогда любая функция $\widetilde{E}({\bf x},t)=F\Big(E({\bf x},t)\Big)$, где $F(E)$ - произвольная дважды дифференцируемая функция одного аргумента $E$, так же является ривертоном.
${\bf Доказательство}$. Пусть $E({\bf x},t)$ - ривертон, а $F(E)$ - произвольная дважды дифференцируемая функция. Тогда имеем следующие тождества:
$$\frac{\partial F(E)}{\partial x^{\alpha}}=F'(E)E_{,\alpha}=F'(E)A_{\alpha}E_t=A_{\alpha}\frac{\partial F(E)}{\partial t}.$$
Эти тождества соответствуют обращению в тождество уравнений (1) и, следовательно, (4) , при подстановке в них в качестве решения функции $\widetilde{E}({\bf x},t)=F\Big(E({\bf x},t)\Big)$.
2.7 Многозначные решения уравнения Д'Аламбера
Среди уравнений (4) , решениями которых являются ривертоны, полезно выделить особый класс, соответствующий условию: $R(E)=|{\ bf A}(E)|=1$. При выполнении такого условия уравнение (4) представляет собой уравнение Д'Аламбера в вещественным координатном пространстве ${\cal R}^n$ . В результате доказывается, что при любом $n>1$ линейное уравнение Д'Аламбера имеет решения в виде ривертонов (2): $$H\Big(E,t+\sum\limits_{\alpha=1}^n n_{\alpha}(E)x^{\alpha}\Big)=0, \tag{17}\label{SolHDA}$$ т.е. многозначные решения. Для случая $n=3$ подобный результат был использован в теории твисторов (см. например, [7, 8]), но для комплексных функций $E$. В данном же случае решения вещественные, если входящие в запись (17) произвольные функции - вещественные/
Таким образом, можно сформулировать следующее:
${\bf Утверждение\ 6}$. Для любого $n>1$ уравнение Д'Аламбера:$$\Delta E = E_{tt},~~~ (\diamondsuit_{1}E=0)$$ имеет решения $E({\bf x},t)$ в виде ривертонов $\{{\cal C}_n,~E(s,t)\}$, структура которого определяется произвольной вектор-функцией ${\bf n}(E):~|{\bf n}|^2=1$ и интегралом движения $H(\xi,\eta)$.
Поскольку уравнение Д'Аламбера линейное, то для него выполняется линейный принцип суперпозиции. Это означает, что любая линейная комбинация ривертонов является решением уравнения Д'Аламбера. Однако при этом следует иметь ввиду то, что каждый ривертон имеет свои области неоднозначности ${\cal V}^n[{\cal C}_n]$. В суперпозиционном решении область неоднозначности будет являться объединением областей неоднозначности отдельных ривертонов. Следует также отметить, что наличие поверхностей, на которых решение типа ривертона становится не однозначным, эквивалентно уравнению Д'Аламбера с сингулярным источником в правой части. Аналогичные конструкции рассматривались в [8]. Подобные построения, по всей видимости, имеют место и в случае нелинейных уравнений (4) общего вида, но требуют отдельного анализа.
2.8 Точные решения многомерных нелинейных телеграфных уравнений и Клейна-Гордона
Ривертоны позволяют строить точные решения других многомерных нелинейных уравнений. Доказательство такого общего утверждения строится на простом анализе суперпозиций ривертонов и некоторых элементарных функций.
Рассмотрим функции следующего вида: $$\Phi({\bf x},t) = G\Big(E + L({\bf k},\omega,{\bf x},t)\Big),$$ где $E$ - ривертон, $L({\bf k},\omega,{\bf x},t)=({\bf k},{\bf x})+\omega t$- линейная функция координат и времени, $G(S)$ - дважды дифференцируемая функция одного аргумента $S(E,{\bf x},t)=\Big(E + ({\bf k},{\bf x})+\omega t\Big)$, ${\bf k}=(k_1,\cdots,k_n)$ - постоянный вектор в ${\cal R}^{n}$, $\omega$ - вещественное число. Имеем следующее общее тождество: $$\diamondsuit_{|{\bf A}|} \Phi = \diamondsuit_{|{\bf A}|} G(S)= G'(S) \diamondsuit_{|{\bf A}|}S + G''(S)\Big[\Big(\nabla S,\nabla S\Big) - |{\bf A}|^2(S_{t})^2\Big].$$ Учитывая свойства ривертонов и линейность функции $L({\bf k},\omega,{\bf x},t)$, имеем: $$\diamondsuit_{|{\bf A}|} S(E,{\bf x},t) = 0,~~L_{tt}=0.$$ Кроме этого, находим:
$$\begin{eqnarray*} && \Big(\nabla S,\nabla S\Big) = 2({\bf k},\nabla E) + |{\bf k}|^2 -|{\bf A}(E)|^2(\omega^2+2\omega E_t)=\\ && =2\Big[({\bf k},{\bf A}(E))-\omega|{\bf A}(E)|^2\Big]E_t+|{\bf k}|^2- |{\bf A}(E)|^2\omega^2. \end{eqnarray*}$$ Отсюда вытекает:
${\bf Утверждение 7}$. Функция $G(S)$, где $S=E+L({\bf k},\omega,{\bf x},t)$, $E$ - ривертон, а $L({\bf k},\omega,{\bf k},t)=({\bf k},{\bf x})+\omega t$ - линейная функция координат и времени с произвольными вещественными коэффициентами ${\bf k},\omega$ при условиях: $$ |{\bf k}|^2=R^2_0={\rm const},~~({\bf k},{\bf A}(E))-R^2_0\omega = \lambda={\rm const},\tag{2.18}\label{CondA1}$$ является решением нелинейного телеграфного уравнения: $$ \diamondsuit_{R_0} G(S) = G''(S)\Big(2\lambda S_t + \mu),\tag{2.19}\label{EqSn}$$ где постоянная $\mu$ имеет следующий вид: $$ \mu = |{\bf k}|^2- \omega^2R^2_0 - 2\omega\lambda.\tag{2.20}\label{CondA2}$$
Решения этого типа будем называть аддитивно модифицированными ривертонами.
${\bf Пример\ 1}$. В случае $\lambda$ уравнение $\ref{EqSn}$ принимает вид нелинейного уравнения Клейна-Гордона: $$\left(\Delta - \frac{\partial^2}{\partial t^2}\right)G(S) = \mu G''(S).$$
В частном случае $G(S)=\ln S$ получаем уравнение Лиувилля: $$\left(\Delta - \frac{\partial^2}{\partial t^2}\right)\ln S = -\frac{\mu}{S^2},$$ а в случае, если функция $G(S)$ удовлетворяет уравнению $G''= \nu^2 G$, приходим к линейному уравнению Клейна-Гордона: $$\left(\Delta - \frac{\partial^2}{\partial t^2}\right)G(S) = \mu \nu^2 G(S).$$ Это указывает на существование решений в форме аддитивно модифицированного ривертона для этого типа уравнений.
${\bf Пример\ 2}$. В случае $\mu=0$ уравнение (\ref{EqSn}) принимает вид нелинейного телеграфного уравнения: $$\left(\Delta - \frac{\partial^2}{\partial t^2}\right)G(S) = \lambda G''(S) S_t.$$ В случае $n=2,3$ эти уравнения имеют отношение к распространению нелинейных электромагнитных волн в среде с нелинейной проводимостью, например, в газах.
Прямым следствием утверждений 5 и 7 является следующее утверждение:
${\bf Утверждение\ 8}$. Функция $G(T)$ , где $T=e^{L({\bf k},\omega,{\bf x},t)}E$, $E$ - ривертон, а , при выполнении тех же условий (\ref{CondA1}) и (\ref{CondA2}) удовлетворяет уравнению:$$\diamondsuit_{R_0} G(T) = \Big(G'(T)+G''(T)T\Big)\left[\Big(\mu - \lambda\omega\Big)T+\lambda T_t\right].\tag{2.21}\label{EqSn1}$$ Этот тип решений будем называть мультипликативно модифицированным ривертоном.
2.9 Системы комплексных квазилинейных уравнений
Расширенная схема описания решений многозначных решений нелинейных уравнений второго порядка опирается на систему комплексных квазилинейных уравнений первого порядка, аналогичных уравнениям (\ref{EqQLn}): $$\frac{\partial E}{\partial x_{\alpha}} = A_{\alpha}({\bf x},t)E_t,\quad\alpha=1,\ldots,n,\tag{2.22}\label{EqQLGn}$$ где ${\bf A}({\bf x},t)=\Big(A_{1}({\bf x},t),\ldots,A_n({\bf x},t)\Big)$ - комплекснозначная вектор-функция координат ${\bf x}=(x_1,\ldots,x_n)$
и времени $t$ . Свойства вектор-функции ${\bf A}$ частично определяются самой формой системы уравнений (\ref{EqQLGn}). При этом оставшийся произвол в выборе вида этой функции определяет характер решений этой системы уравнений. В частности, в [1] исследовалась вещественная вектор-функция ${\bf A}$ вида: ${\bf A}={\bf A}(E)$, что позволяет построить общий вид решений (\ref{EqQLGn}) такого выбора вектор-функции ${\bf A}$ и установить связь между этими уравнениями и нелинейными волновыми уравнениями второго порядка. Такая связь устанавливается с помощью вычисления дифференциальных следствий (\ref{EqQLGn}) .
Вычисляя дивергенцию от уравнений (\ref{EqQLGn}) , находим: $$\Delta E = \Big({\rm div} {\bf A} - \frac{1}{2}\frac{\partial}{\partial t}{\bf A}^2\Big) E_t + \frac{\partial}{\partial t}\Big({\bf A}^2 E_t\Big).\tag{2.23} \label{EqGenP2}$$ Таким образом, можно сформулировать следующее:
${\bf Утверждение\ 1}$. Каждое решение $E({\bf x},t)$ системы уравнений (\ref{EqQLGn}) , имеющее в заданной области производные второго порядка, является так же решением уравнения (\ref{EqGenP2}) . В общем случае это уравнение относится к классу телеграфных уравнений и имеет гиперболический характер. В случае выполнения условия: $${\rm div}{\bf A}-\frac{1}{2}\frac{\partial}{\partial t}{\bf A}^2 = 0\tag{2.24}\label{EqDivA}$$
это уравнение будет чисто гиперболическим, что вполне согласуется с тем, что решениями его являются решения гиперболической системы первого порядка (\ref{EqQLGn}). В частности, уравнение (\ref{EqDivA}) обращается в тождество при условии ${\bf A}={\bf A}(E)$, где $E$ удовлетворяет уравнению (\ref{EqQLGn}), что и было рассмотрено в [1].
- Войдите на сайт для отправки комментариев
- 5165 просмотров