I. Цели второго годичного этапа

Целью очередного этапа работ по проекту является решение следующих задач:
1. Построение и исследование с помощью метода обобщенных подстановок Коула-Хопфа (МОПКХ) новых моделей динамики самогравитирующей среды со сферической симметрией при произвольных начальных распределениях скорости и плотности потока. Исследование возможности построения точных решений динамики самогравитирующей среды в рамках МОПКХ с политропическим уравнением состояния.

2. Построение и исследование трехмерных течений сжимаемой идеальной жидкости с помощью трехмерного варианта МОПКХ и уравнений бессдвиговой конгруэнции. Классификация возможных типов нарушения структуры конгруэнций.

3. Исследование с помощью МОПКХ ионно-звуковых волн и других типов нелинейных волн в плазме

4. Исследование новых типов нелинейных динамических систем, линеаризуемых с помощью МОПКХ на подалгебрах GLn. Исследование связи структуры базовой алгебры со свойствами динамических систем и ее законами сохранения.

5. Разработка алгоритмов и программ применения сеточных уравнений, линеаризуемых с помощью МОПКХ, к построению эмпирических моделей процессов по данным в форме цифровых рядов наблюдений и изображений.

6. Исследование случайно-возмущенных конечно-мерных динамических систем с помощью метода максимальной энтропии. Выяснение общих свойств состояний с максимальной энтропией таких систем и их устойчивости. Вывод термодинамических свойств таких систем.

II. Ожидаемые в конце 2012 г. научные результаты

В конце очередного этапа выполнения проекта предполагается получить следующие результаты:

1) Построение и анализ точных решений динамики самогравитирующей среды для начальных распределений скорости и плотности, удовлетворяющих условиям, наблюдаемым в реальных системах. Будут выяснены основные характеристики процесса сжатия облаков пыли в собственном поле тяготения такие, как зависимость времени образования сингулярности от параметров начальных распределений. Будет дан ответ на вопрос - можно ли в рамках такого подхода строить точные решения для процесса сжатия газо-пылевого облака с политропическим уравнением состояния? Это даст возможность строить точные решения со стабилизацией процесса сжатия газопылевого облака при возрастании давления.

2) При исследовании трехмерных течений сжимаемой жидкости с помощью уравнений бессдвиговой конгруэнции будет дан ответ на вопрос о возможной структуре вихревых образований, связанных с различными типами нарушения конгруэнций. Полученные результаты могут быть применены для описания вихревых структур в атмосфере типа торнадо. Предполагается в рамках этих исследований построить точные решения, описывающие частицы с зарядом и собственным магнитным полем, имеющие отношение к топологической квантовой теории.

3) Предполагается, что в рамках работ по исследованию интегрируемых с помощью МОПКХ динамических систем будет дана классификация таких систем для матричных алгебр небольшой размерности. Будут построены системы их законов сохранения и выяснена связь этих законов сохранения со структурой алгебр. Предполагается, что данные результаты будут применены к анализу реальных механических и физических систем, таких как нелинейно связанные осцилляторы и системы взаимодействующих тел.

4) В результате работ, связанных с исследованием сеточных уравнений, линеаризуемых с помощью МОПКХ, будут построены и опробированы в тестовых режимах алгоритмы и программы построения эмпирических моделей процессов, представленных цифровыми рядами наблюдений и изображений. Предполагается, что это даст новые методы построения нелинейных моделей прогноза изменчивости наблюдаемых природных процессов, обобщающих современные линейные методы типа авторегрессионных.

5) В рамках работ по применению метода максимальной энтропии к случайно-возмущенным конечно-мерным динамическим системам будет развит аппарат анализа состояний с максимальной энтропией в форме уравнений, что позволит строить термодинамические соотношения для параметров таких систем вблизи положения равновесия. Предполагается, что такой подход позволит дать ответ о числе и типе состояний с максимумом энтропии. Метод предполагается приложить к задачам небесной механики и динамики искусственных спутников Земли.

6) Предполагается применить МОПКХ к задачам волновой динамики плазмы. Предполагается, что будут получены новые точные решения в задаче о динамике ионно-звуковых волн, и магнито-звуковых волн в плазме при наличии внешнего магнитного поля. Это позволит более глубоко разобраться в эволюции волновых процессов в плазме в нелинейном режиме.

 

III. Развернутый отчет (Часть I)

III.1. Волны в самогравитирующей среде. Анализ решений

III.1.1. Цилиндрические и сферические волны

По аналогии с одномерным течением идеальной сжимаемой среды (см. Отчет 2011) решается задача о цилиндрических и сферических волнах в самогравитирующей среде. Уравнения динамики такой среды можно представить в следующем виде: $$u_t + uu_r =-\phi_r\hspace{3cm}(1.2.1)$$ $$\rho_t+\frac{1}{r^n}\frac{\partial}{\partial r}\Big( r^n\rho u\Big)=0;\hspace{2cm}(1.2.2)$$ $$\frac{1}{r^n}\frac{\partial}{\partial r}\Big(r^n\phi_r\Big) = 4\pi G \rho.\hspace{3cm}(1.2.3)$$ При $n=0$ эта система переходит у уравнение для одномерного течения, при $n=1$ течение обладает цилиндрической симметрией, а при $n=2$ - сферической.

Введем функцию $\varrho = r^n\rho$, которая представлет собой с точностью до постоянного множителя радиальную плотность среды, т.е. массу, отнесенную к бесконечно тонкому цилидрическому ($n=1$) или сферическому ($n=2$) слою среды. В результате система уравнений примет следующий вид: $$u_t + uu_r =-\phi_r;$$
$$\varrho_t+\frac{\partial}{\partial r}\Big(\varrho u\Big)=0;\hspace{3cm}(1.2.4)$$
$$\frac{\partial}{\partial r}\Big(r^n\phi_r\Big) = 4\pi G \varrho.\hspace{3cm}(1.2.5)$$ Вид этой системы позволяет применить для построения ее решений метод гидродинамических подстановок, изложенный в статье: Журавлев В.М. Точные решения в гидродинамике сжимаемой жидкости и методы функциональных подстановок типа Коула-Хопфа. Сб. Инновационные технологии. Под ред. проф. С.В. Булярского. Ульяновск. Изд. УлГУ, 2010 г., С. 77-93 .

Введем следующие подстановки: $$u=-\theta_t/\theta_r$$ $$\varrho = \theta_r$$. Тогда уравнение Пуассона сводится к уравнению следующего вида: $$\phi_r = \frac{1}{r^n} \Big(4\pi G \theta + g_0(t)\Big). \hspace{3cm}(1.2.6)$$ Рассмотрим случай $g_0\equiv 0$. Используя это соотношение, преобразуем первое уравнение в системе. Находим: $$u_t + uu_r =-\frac{4\pi G}{r^n}\gt.\hspace{3cm}(1.2.7)$$ Решение этого уравнения для $u(r,t)$ будем искать в таком виде: $$u = f(r)Q(\theta).\hspace{3cm}(1.2.8)$$  Подставляя это соотношение в (1.2.7), находим условия, при которых оно обращается в тождество: $$\acute{f}f=-r^n$$ $$Q^2(\theta)=4\pi G \theta.$$ Отсюда следует, что для обращения (1.2.7) в тождество достаточно выбрать: $$Q(\theta)=\sqrt{4\pi G\theta}$$ и $$f(r)=\pm \left\{\begin{array}{l}\sqrt{2}\sqrt{r^{-1}_0+ r^{-1}},~~n=2\\ \sqrt{2}\sqrt{\ln r_0 - \ln r},~~n=1.\end{array}\right.$$ Здесь $r_0$-постоянная интегрирования. При этом функция $\theta(r,t)$ должна удовлетворять уравнениям: $$\theta_t \pm \Big(\sqrt{8\pi G} \sqrt{r^{-1}_0+r^{-1}}\sqrt{\theta}\Big)\theta_r = 0.\hspace{0.5cm}n=2\hspace{3cm}(1.2.9)$$ $$\theta_t \pm \Big(\sqrt{8\pi G} \sqrt{\ln r_0 - \ln r}\sqrt{\theta}\Big)\theta_r = 0.\hspace{0.5cm}n=1\hspace{3cm}(1.2.10)$$ Эти уравнения имеют интегралы движения.

III.1.2. Вывод интегралов движения 

Для вывода интегралов движения рассмотрим следующее неявное алгебраическое уравнение: $$H\Big(\theta,x-X(\theta,t)\Big) = 0. \hspace{3cm}(1.3.0)$$ Здесь $H(\xi,\eta)$ - некоторая дифференцируемая функция двух аргументов и $\eta=x-X(\theta,t)$.  Дифференцируя это уравнение по $x$ и $t$, приходим к двум соотношениям: $$H_x = H_{\xi} \theta_x + H_{\eta}\eta_x = H_{\xi} \theta_x + H_{\eta}\left(1-\frac{\partial X}{\partial \theta}\theta_x\right)=0,$$ $$H_t = H_{\xi} \theta_t + H_{\eta}\eta_t = H_{\xi} \theta_x - \left(\frac{\partial X}{\partial t}- \frac{\partial X}{\partial \theta}\theta_t\right)H_{\eta}=0.$$ Исключая производные $H_{\xi}$ и $H_{\eta}$, получаем: $$\theta_t+\frac{\partial X}{\partial t}\theta_x=0.\hspace{3cm}(1.3.1)$$

Сделаем в уравнениях (1.2.9) и (1.2.10) замену координатной переменной, полагая: $$dz=\frac{dr}{\sqrt{8\pi G} \sqrt{r^{-1}_0+r^{-1}}},\hspace{0.5cm}n=2$$ $$dz=\frac{dr}{\sqrt{8\pi G} \sqrt{\ln r_0 - \ln r}},\hspace{0.5cm}n=1$$. Тогда уравнения для $n=1$ и $n=2$ будут иметь одинаковый вид: $$\theta_t \pm \sqrt{\theta}\theta_z = 0.\hspace{3cm}(1.3.2)$$ Сравнивая это уравнение с (1.3.1), находим вид соответствующей функции $X(\theta,t)$. Имеем: $$\frac{\partial X}{\partial t}=\pm\sqrt{\theta}.\hspace{3cm}(1.3.3)$$  Отсюда: $$X(\theta,t)=\pm t\sqrt{\theta}$$. Таким образом, общий интеграл движения уравнений имеет следующий вид: $$H(\theta,z(r)\mp t\sqrt{\theta})=0$$.

III.1.3. Джинсовская неустойчивость в одномерном случае 

Полученные результаты позволяют на точных решениях рассмотреть динамику локальных возмущений плотности под действием собственного поля тяготения в одномерном случае. Эта задача о джинсовской неустойчивости самогравитирующей среды важна для описания динамики крупномасштабной структуры Вселенной. При анализе формирования крупномасштабной структуры предполагают, что точками среды являются галактики. При этом давление в такой среде равно нулю, что соответствует уравнению состояния пыли $p=0$. Кроме этого вязким трением в такой среде можно пренебречь. В результате динамика таких систем описывается в точности системой уравнений  (1.2.1) - (1.2.3). Решения, полученные в предыдущем параграфе, позволяют строить точные решения этой задачи при заданных начальных условиях распределения плотности и скорости потока. Начальные условия в этом случае задаются соотношениями: $$\rho(x,0)= \frac{\partial \theta_0(x)}{\partial x},\hspace{1cm}u(x,0) = F(\theta_0(x)) -c(0),$$ где $\theta_0(x) = \theta(x,0)$ - начальное распределение функции $\theta(x,t)$.

Для получения физически понятных решений необходимо предварительно выяснить то, какие распределения плотности, скорости и гравитационного потенциала допустимы с физической точки зрения. Основным требованием, ограничивающим выбор функции  $\theta_0(x)$,  является неотрицательность плотности жидкости во всех точках пространства: $\rho \ge 0$. В этом случае имеем: $$\theta(x,t) -\Theta_0(t)=\int\limits_{-\infty}^x\rho(x,t)dx \ge 0.$$ Из уравнения Пуассона следует соотношение  (1.2.6) , которое связывает функцию с ускорением свободного падения в точке с координатой.  Отсюда следует: $$\phi_x \ge g_0(t)+4\pi G \Theta_0(t).\hspace{3cm}(1.3.1)$$ По своему смыслу   $-\phi_x$ является ускорением свободного падения в точке пространства с координатой $x$. Из физических соображений естественным выбором функции  $g_0(t)$ является такой, при котором ускорение свободного падения было бы равно нулю при $x\to \pm\infty$. Физически это связано с требованием $\rho\to 0$ в этих же пределах. Однако, если полагать: $$\lim\limits_{x\to-\infty}\phi_x = 0,$$ то тогда из соотношения  (1.3.1) следует, что при $x\to +\infty$ ускорение свободного падения стремится к некоторой отрицательной постоянной, равной $$g_{\infty} = -4\pi G M,$$ где $$M = \int\limits_{-\infty}^{\infty}\rho(x,t) dx \ge 0$$ есть полная масса материи в пространстве. Поскольку $\rho \ge 0$, то отсюда следует, что в одномерном случае локализованное возмущение плотности создает на бесконечности постоянное поле тяготения. Выбор граничных значений напряженности гравитационного поля на бесконечности определяет в реальности значение скорости, которую приобретает сформировавшаяся структура при  $t\to\infty$. Если $g_{\infty} \not= g_{-\infty}$, то центр масс всей системы приобретает некоторое ускорение. Это ускорение такое, что в системе, движущейся вместе с центром масс  $\acute{g}_{\infty} = \acute{g}_{-\infty}$. Здесь $\acute{g}_{\infty},~ \acute{g}_{-\infty}$  - величины ускорения на бесконечности в системе центра масс.

Пример 1.

В качестве примера демонстрации некоторых важных эффектов в одномерном случае рассмотрим начальное распределение плотности, которое задается простой функцией $\theta_0(x)$  следующего вида: $$\theta_0(x) = \frac{M}{2} (\th(kx)+1),$$ где $k\ge 0$ - произвольное положительное вещественное число, величина которого обратно пропорциональна характерному пространственному размеру$L$ области, занятой материей: $L=k^{-1}$. Рассмотрим в качестве начального распределения скорости среды функцию $u(x,0)=0$. При таком выборе $g_{-\infty}=0,~~g_{\infty}=-4\pi G M.$ При этом начальное распределение плотности и скорости будут иметь следующий вид: $$\rho(x,0) = \frac{Mk}{2\ch^2(kx)}\ge 0,\hspace{1cm}u(x,0)=0.$$ В этом случае решение задачи о динамике такого возмущения дается в неявном виде как решение алгебраического трансцендентного уравнения: $$\theta=\frac{M}{2}\left[\th\left(k\Big(x+\mu_0\theta t^2\Big)\right)+1\right].\hspace{3cm}(3.2)$$ Здесь $\mu_0=2\pi G$. Решения для плотности и скорости потока можно получить из интеграла движения. Дифференцируя  (1.3.2) по   $x$ и $t$, находим $$\rho=\theta_x=\frac{M k}{4\ch^2\left(k\Big(x+\mu_0\theta t^2\Big)\right)-2Mk t^2\mu_0},\qquad u = - 2\mu_0 t \theta.$$ На рис. 1 и 2 представлены распределения плотности в последовательные моменты времени $t=0,2,4,6,8,0.95$. Начальные распределения соответствуют на рисунках моменту времени $t=0$.

 

 

 

 

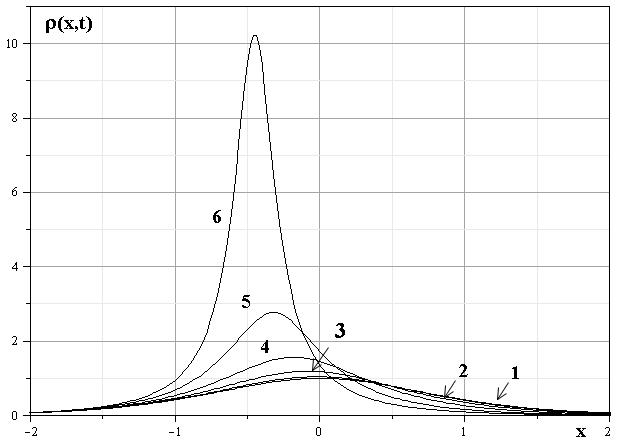
Рис.  1: Эволюция распределения скорости (a) для начальных распределений  (1.3.2)

 

 

 

 

 

 

 

Рис.  2: Эволюция распределения  плотности для начальных распределений  (1.3.2)

 

 

 

 

В этом примере центр  масс системы ускоряется влево. Графики распределений показаны вплоть до момента времени, когда в центре масс системы образуется сингулярность. Время $t_{*}$ до образования сингулярности для данного распределения определяется  соотношением: $$t_{*}=\sqrt{\frac{2}{kM\mu_0}}=\sqrt{\frac{L}{\pi G M}}.$$

 

Пример 2.

Аналогичные результаты можно получить для начальных распределений плотности и скорости среды следующего вида:  $$\rho(x,0) = \frac{M}{\pi(1+k^2x^2)} > 0,\hspace{1cm}u(x,0)=0.\hspace{3cm}(1.3.3)$$  Распределения в произвольный момент времени вычисляются из следующих соотношений: $$\theta=\frac{M}{\pi}\arctg\Big(k\Big(x+\mu_0\theta t^2\Big)\Big),$$ $$\rho=\theta_x=\frac{M k}{\pi+\pi k^2\Big(x+\mu_0\theta t^2\Big)^2-Mk t^2\mu_0},\qquad u=-2\mu_0 t \theta$$. Эти распределения представлены на рис. 3 и 4.

 

 

 

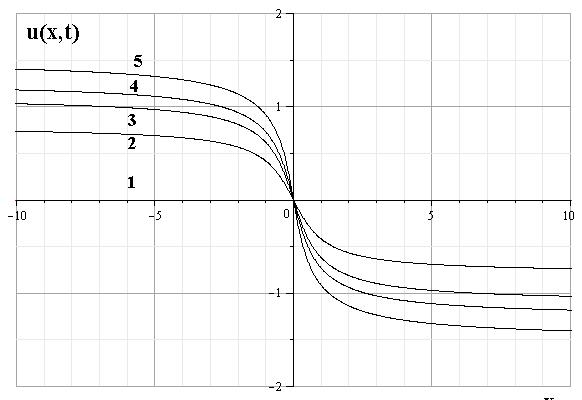
Рис.  3: Эволюция распределения  скорости для начальных распределений  (1.3.3)

 

 

 

 

Рис.  4: Эволюция распределения  плотности для начальных распределений  (1.3.2)

 

 

 

 

 

В этом примере центр масс всей системы покоится. Время $t_{*}$ до образования сингулярности для данного распределения определяется  соотношением: $$t_{*} = \sqrt{\frac{\pi}{kM\mu_0}}=\sqrt{\frac{L}{G M}}.$$

III.1.4. Джинсовская неустойчивость в сферическом случае

При анализе модели эволюции сферически симметричного начального распределения плотности необходимо определить подходящую форму интеграла движения. Исходя из необходимости задавать начальное распределение плотности, общую форму интеграла движения полезно задавать в следующем виде: $$\theta=\frac{M}{4\pi Q_0} Q(\chi(r,t)).\hspace{3cm}(1.4.1)$$ Здесь $M$ - полная масса вещества во всем пространстве, $$Q_0 = \int\limits_{0}^{\infty} Q'(r)dr = Q(\infty)-Q(0)$$ и $$\chi(r,t)=r^{3/2} \pm \sqrt{8\pi G} t\sqrt{\theta}.$$ В этом случае функция $Q(\chi)$  задает форму начального распределения функции  $\theta$ и в конечном итоге плотности, которая вычисляется в этом случае так: $$\rho(r,t) = \frac{3M}{4\pi Q_0 r^{3/2}} \frac{\sqrt{\theta}\acute{Q}\Big(\chi(r,t)\Big)}{8\pi G\sqrt{\theta} \mp M \sqrt{4\pi G}\acute{Q}\Big(\chi(r,t)\Big) t}.\hspace{1cm}\acute{Q}=\frac{dQ(\chi)}{d\chi}.$$ Множитель $M(4\pi Q_0)^{-1}$  в  (1.4.1) выбирался из условия: $$M = 4\pi\int\limits_0^{\infty} \rho r^2 dr.$$

Выбор самой функции $Q(\chi)$ должен определяться требованиями $0\le Q_0\le \infty$  и условия монотонного неубывания этой функции с ростом. Кроме этого, исходя из того, что, по крайней мере, в начальный момент времени в начале координат должна отсутствовать сингулярность в распределении плотности вещества ($\rho=\theta_r/r^2$), зависимость  $Q(\chi)$ должна быть такой, что: $$Q\Big(\chi(r,0)\Big) = K(r^3).$$ Здесь $K(s)$   - всюду непрерывная монотонно неубывающая функция, равная 0 при $s=0$: $K(0)=0$. Эти условия обеспечивают конечность плотности среды в точке $r=0$ в начальный момент времени.

Следуя полученным требованиям по аналогии с одномерным случаем рассмотрим два простых примера, сооотвествующих двум различным начальным распределениям плотности и скорости.

Пример 1

Рассмотрим в качестве интеграла движения следующее соотношение для $\theta$: $$\theta(r,t) = \frac{M}{4\pi}\th\left(k\Big(r^{3/2}+ \sqrt{8\pi G}t\sqrt{\theta}\Big)^2\right).$$ Этот интеграл движения соответствует следующим начальным распределениям: $$\theta_0(r,0)=\frac{M}{4\pi}\th\left(kr^3\right),$$ $$\rho(r,0)=\frac{3Mk}{4\pi\ch^2(kr^3)}\ge 0,\qquad u(r,0)=-\sqrt{8\pi G}r^{-1/2}\theta_0(r).$$ Неотрицательное число $k$ представляет собой величину, обратную характерному пространственному масштабу $L=k^{-1}$ начальной флуктуации. Решение, соответствующее  этим начальным распределениям, имеет такой вид:$$\rho(r,t) = \frac{3Mk\sqrt{\theta}\Big(1+\mu_0 t \sqrt{\theta} r^{-3/2} \Big)}{4\pi \sqrt{\theta} \ch^2(k\chi^2(r,t)) - Mk \mu_0 t \chi(r,t)},\hspace{0.5cm}u(r,t) = - \mu_0 \sqrt{\theta}.\hspace{1cm}(1.4.2)$$  Здесь $\chi(r,t)=r^{3/2}+ \mu_0 t\sqrt{\theta}$, $\mu_0= \sqrt{8\pi G}$.

 

 

 

 

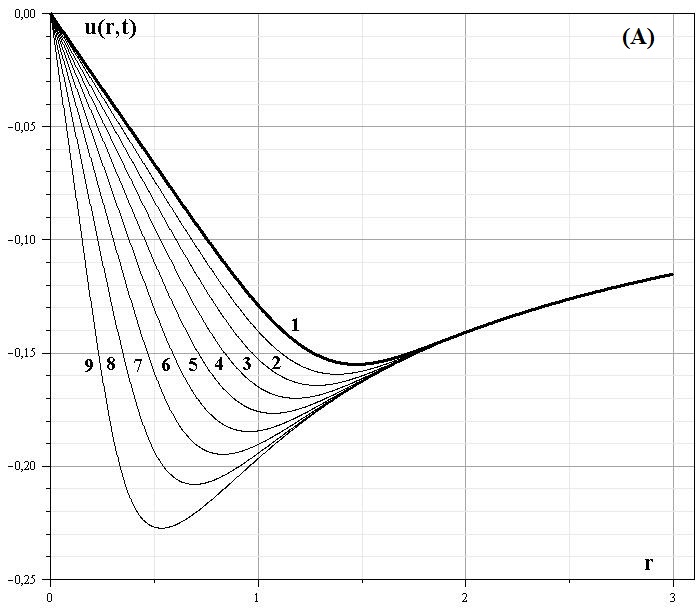
Рис.  5: Эволюция распределения  скорости для начальных распределений  (1.4.2)

 

 

 

 

 

 

 

 

 

 

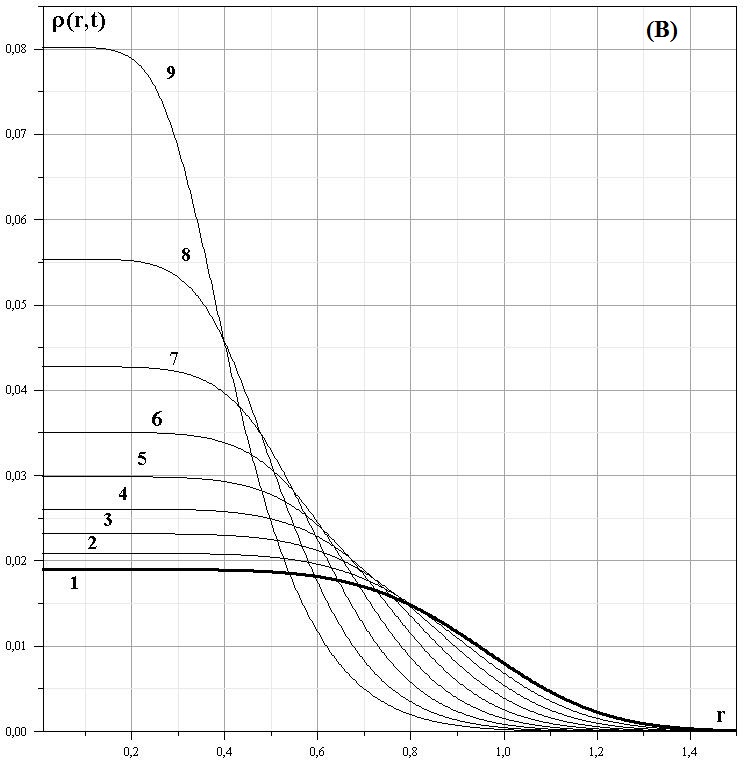
Рис.  6: Эволюция распределения  плотности для начальных распределений  (1.4.2)

 

 

 

 

 

 

 

 

 

 

Пример 2

Для начальных распределений: $$\theta_0(r,0) = \frac{M}{2\pi^2}\arctg{(kr^3)},$$ $$\rho(r,0) = \frac{3Mk}{4\pi}\frac{1}{1+k^2r^6}\ge 0,\hspace{1cm}u(r,0)=0.$$  интеграл движения записывается в такой форме: $$\theta(r,t) = \frac{M}{2\pi^2}\arctg\left(k\Big(r^{3/2}+ \sqrt{8\pi G} t\sqrt{\theta}\Big)^2\right),\hspace{3cm}(1.4.3)$$ Здесь $Q_0=\pi/2$. Распределения в последующие моменты времени представлены на рис. 7 и рис. 8.

 

 

 

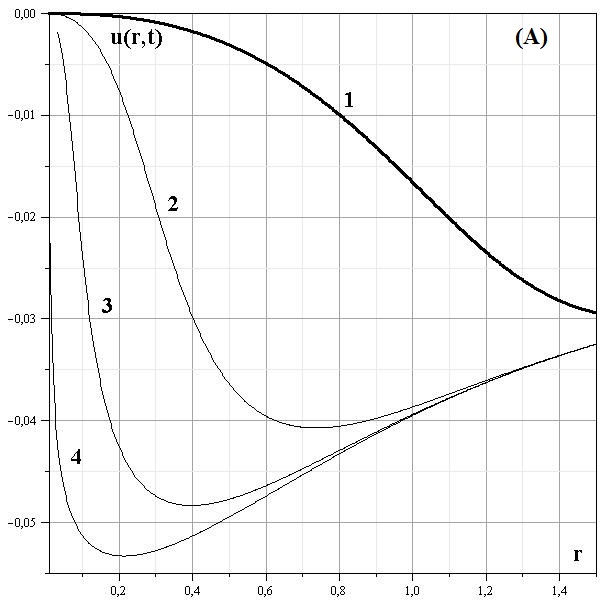
Рис.  7: Эволюция распределения  скорости для начальных распределений  (1.4.3)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

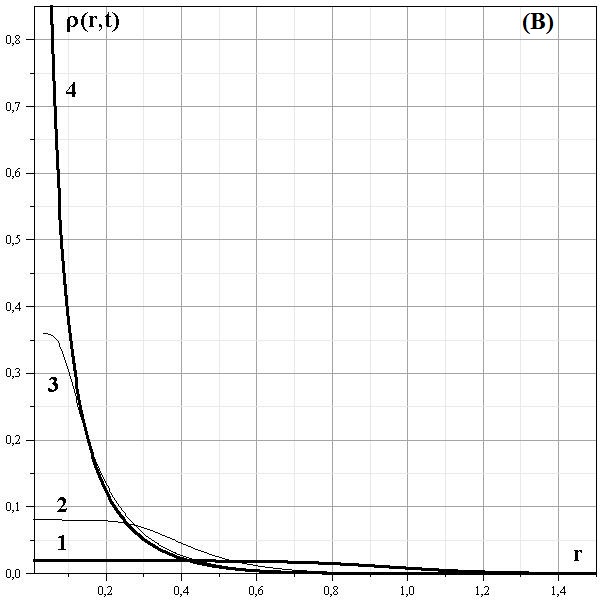
Рис.  8: Эволюция распределения  плотности для начальных распределений  (1.4.3)

 

 

 

 

 

 

 

 

Асимптотический анализ

Разложение функций $u(r,t)$ и $\rho(r,t)$  в ряд вблизи точки $r=0$ имеет вид: $$\theta=r^{3}\Big(\theta_0(t) + \theta_4(t) r^6 + O(r^{12})\Big),$$ $$\rho= 3\theta_0(t) + 9 \theta_4(t) r^6 + O(r^{12}).$$  Из уравнения (4.2) следует уравнение для функции $\theta_0(t)$: $$\theta_0=\frac{M k}{4\pi} (1+ \sqrt{\theta_0} t \mu_0)^2,$$ где $\mu_0 = 4\pi G $. Это уравнение имеет следующий вид: $$\theta^{\pm}_0(t)=\frac{M k}{4\pi(1\pm \mu_0 t\sqrt{M k/4\pi})}.$$ Из этого соотношения находятся все остальные коэффиценты разложения. Одно из этих решений за конечное время $t_*$ обращается в бесконечность, что соответствует образованию сингулярности в распределении плотности среды. Время образования сингулярности равно: $$t_*=\sqrt{\frac{4\pi}{M k}}\frac{1}{\mu_0}$$ Второе решение не имеет физического смысла.

III.2. Волны зарядовой плотности в вакуумном диоде   

Задача о токе в диоде, возникающем под действием разности потенциалов на электродах (между анодом и катодом), является классической задачей теории волн зарядовой плотности и электронных пучков [1, 2, 3]. Эта задача возникла при описании тока в вакуумных электроннолучевых приборах, например, лампах, но имеет гораздо большую область применения.

Основной проблемой, связанной с описанием тока в диоде, является учет влияния распределенного заряда, движущегося между электродами. Наличие областей с максимумом концентрации распределенного заряда в области движения заряженных частиц называют часто виртуальным катодом. Появление виртуального катода ограничивает ток в диоде (предел Чайлда-Ленгмюра), что приводит к специфическому изменению вольт-амперной характеристики диода.

Одним из способов описания явлений, происходящих в таких приборах, является подход, основанный на гидродинамической модели движения заряженной жидкости, находящейся во внешнем и собственном электрическом поле [4, 5, 6]. Обычно такая система уравнений решается с помощью различных приближенных или численных методов (см. например, [7, 8]). Однако для анализа всех особенностей явлений образования виртуального катода желательно иметь точные решения самосогласованной задачи, которая проанализирована в настоящее время лишь в стационарном случае [4, 5, 6]. В настоящей работе для решения системы уравнений динамики волн зарядовой плотности в диоде используется метод гидродинамических подстановок, изложенный в работе [9] и использованный для решения задачи о динамике самогравитирующей пылевой среды [12]. Этот метод восходит к теории обобщенных подстановок Коула-Хопфа [10, 11, 12] и модифицирован специально для решения гидродинамических задач с переменной плотностью. В настоящей работе строятся точные решения общего вида в задаче о волнах зарядовой плотности в вакуумном диоде и на некоторых простых примерах анализируются основные выводы из этой теории.

III.2.1. Уравнения токопереноса в вакуумном диоде

Рассмотрим одномерную модель диода, в котором под действием разности потенциалов $\phi_{1}(t)$ на двух ограничивающих электродах существует ток с плотностью $j(x,t) = q n(x,t) v(x,t)$ , где $n$  -- концентрация частиц, имеющих заряд $q$ и массу $m$, так что $\rho_e=q n(x,t)$  -- плотность заряда, а $\rho_m = m n(x,t)$   -- плотность массы. Величина  $v(x,t)$ -- скорость частиц. Потенциал $\phi(x,t)$  меняется непрерывно между электродами от значения  $\phi(0,t)=0$ на одном электроде до значения   $\phi(d,t)=\phi_1(t)$ на другом. Величина  $d$ -- расстояние между электродами. Систему уравнений, описывающую динамику возникающего токопереноса, можно записать в виде трех уравнений (см. [4]):

$$n_t+\Big(n v\Big)_x=0, \hspace{3cm} (2.1)$$
$$v_t+vv_x=-\frac{q}{m}\phi_x, \hspace{3cm} (2.2)$$
$$\phi_{xx} = -4\pi q n. \hspace{3cm} (2.3)$$
Первое уравнение представляет собой закон сохранения заряда, второе -- уравнение Эйлера течения идеальной заряженной жидкости, третье -- уравнение Пуассона для потенциала электрического поля, созданного распределенным в пространстве зарядом. Граничные условия для тока в области переноса имеют следующий вид:

$$\phi(0,t)=0,~~\phi(d,t)=\phi_1(t),$$
$$v(0,t)=v_0(t),~~n(0,t)=n_0(t).$$
В качестве начальных условий следует задавать начальные распределения в пространстве плотности заряда $n(x,0)=N_0(x)$ и скорости $v(x,0)=U_0(x)$.

III.2.2. Гидродинамические подстановки для концентрации и скорости потока

Следуя работам [9, 12], рассмотрим вспомогательное уравнение:

$$\theta_t+v\theta_x=0, \hspace{3cm} (2.4)$$
где функция $\theta$ играет ключевую роль в методе построения решений. Смысл введения этой функции определяется следующими соображениями. Дифференцируя уравнение (2.4), приходим к уравнению:

$$\frac{\partial}{\partial t}\theta_x+\frac{\partial}{\partial x}\Big(v\theta_x\Big)=0,$$  
которое при условии  $n=\theta_x$ превращается в уравнение неразрывности  (2.1) .

Следующий шаг в построении решения состоит в интегрировании уравнения Пуассона  (2.3) . Используя подстановку $n=\theta_x$ и интегрируя (2.3) , находим:

$$\phi_x = -4\pi q \theta - e_0(t), \hspace{3cm}(2.5)$$
где $e_0(t)$ -- функция $t$, связанная с начальными условиями. Используя последнее соотношение, для скорости потока $v(x,t)$  получаем уравнение:

$$v_t+vv_x =\Gg \theta + g_0(t) \hspace{3cm} (2.6)$$
Здесь $\Gg=4\pi q^2/m$  и $g_0(t)=(q/m) e_0(t)$ . Будем искать решение для $v$  в виде:

$$ v(x,t) = V(\theta)+\Gg t\theta+u_0(t) \hspace{3cm} (2.7)$$
Подставляя это соотношение в левую часть  (2.6) и учитывая то, что функция $\theta$ по определению связана с   соотношением  (2.4), получаем:

$$v_t+vv_x = (V_{\theta}(\theta)+\gamma t)\Big(\theta_t+v\theta_x\Big)+\gamma\theta+\dot{u}_0=\gamma\theta+\dot{u}_0.$$
В результате уравнение (2.6) обращается в тождество при условии $g_0(t)=\dot{u}_0$. Используя теперь связь (2.4), приходим к уравнению для функции $\theta$:

$$\theta_t+\Big(V(\theta)t+\gamma\theta+u_0(t)\Big)\theta_x=0.\hspace{3cm} (2.8)$$

III.2.3. Интеграл движения 

Уравнение (8) представляет собой вариант гиперболического уравнения Хопфа (1.3.1), общий интеграл которого задается с помощью следующего алгебраического уравнения ( см. соотношение (1.3.0)):

$$h\Big(\theta,x-V(\theta)t-\gamma t^2\theta/2-x_0(t)\Big)=0, \hspace{3cm}(2.9)$$
где $h(\xi,\eta)$ -- произвольная дифференцируемая функция двух аргументов $\xi=\theta(x,t)$ и $\eta=x-V(\theta)t-\Gg t^2\theta/2-x_0(t)$, $\dot{x}_0(t)=u_0(t)$. Дифференцируя (2.9) по $x$ и $t$, приходим к двум уравнениям:

$$h_{\xi}\theta_x+h_{\eta}\Big(1-V_{\theta}(\theta)\theta_x-\gamm t^2\theta_x/2\Big)=0,$$
$$h_{\xi}\theta_t+h_{\eta}\Big(-V_{\theta}(\theta)\theta_t-\gamma t^2\theta_t/2-V(\theta)-\gamma t\theta-\dot{x}_0\Big)=0.$$
Исключая из этих уравнений необращающиеся тождественно в ноль производные $h_{\xi}$ и $h_{\eta}$, приходим к уравнению (2.8) и условию $\dot{x}_0(t)=u_0(t)$. Функцию $x_0(t)$  будем называть смещением потока заряженных частиц.

Уравнение  (2.9) без ограничения общности удобно представить в следующем виде:

$$ \theta = H\Big(x-V(\theta)t-\gamma t^2\theta/2-x_0(t)\Big). \hspace{3cm} (2.10)$$
Вид функции $H(\eta)$ задается начальным распределением функции $\theta$ :

$$\theta(x,0) = H(x-x_0(0)),$$
что, в свою очередь, определяется начальным распределением концентрации частиц:

$$n(x,0)=\left.\theta_x\right|_{t=0}=\frac{\partial}{\partial x}H(x-x_0(0)).$$
При этом начальное распределение скорости определяет вид функции $V(\theta)$, исходя из соотношения:

$$v(x,0)=V\Big(\theta(x,0)\Big)+\dot{x}_0(0).$$
Распределение потенциала в начальный момент времени определяется распределением плотности заряда:

$$\phi(x,0) = -4\pi q \int\limits_{0}^{x}\theta(x,0) dx - \frac{m}{q}\ddot{x}_0(0) x + \phi_0(0).\hspace{3cm}(2.11)$$
Таким образом, мы получаем полное решение задачи с начальными условиями (задача Коши).

III.2.4. Решение граничной задачи

Вычислим теперь значение потенциала на границах области, т.е. в точках  $x=0$ и $x=d$. Имеем:

$$\phi(0,t)=0=\phi_0(t),$$
$$\phi(d,t)= -4\pi q \int\limits_{0}^{d}\theta(x,t) dx -\frac{m}{q} \ddot{x}_0(t) d = \phi_1(t).$$
Из последнего соотношения находим:

$$\ddot{x}_0(t) = -\frac{q}{md}\phi_1(t)-\frac{\gamma}{d}\int\limits_{0}^{d}\theta(x,t) dx. \hspace{3cm}(2.12)$$
в конечном итоге, это уравнение определяет ток в точке  $x=d$:

$$j_1(t)=qn(d,t)v(d,t) = q\theta_x(d,t)\Big(V(\theta(d,t))+\gamma t\theta(d,t)+\dot{x}_0(t)\Big).$$
Зависимость $j_1=j_1(\phi_1)$ определяет вид вольт-амперной характеристики диода, что является наиболее важным приложением модели, описываемой уравнениями (2.1) - (2.3)

Для анализа уравнения (2.12) необходимо иметь общее представление для интеграла в его правой части. Его можно получить, предполагая выполнение некоторых упрощающих условий. В качестве такого условия рассмотрим требование, что в начальный момент все заряженные частицы обладают во всем пространстве одинаковой скоростью, т.е.:

$$v_0(x,0)=W_0={\rm const}.$$
Из этого условия следует: $V(\theta)=0$. Тогда начальное распределение функции $\theta$ , определяемое плотностью заряда, задается одной функцией $\theta(x,0)=H(x-x_0(0))$. В этом случае удобно интеграл движения  (2.10) переписать в следующем виде:

$$x-x_0(t)-\gamma t^2 \theta/2 = F(\theta),$$
где $F\theta)$ -- функция обратная $H(\eta)$. Дифференцируя это соотношение по $x$, после несложных преобразований находим:

$$n=\theta_x=\frac{1}{F_{\theta}(\theta)+\gamma t^2/2}. \hspace{3cm}(2.13)$$

Из этого соотношения сразу следует, что для начальных распределений параметров в рассматриваемой системе не происходит опрокидывания фронта волны зарядовой плотности. Момент опрокидывания  $t_*$ и координата $x_*$ возникновения разрыва фронта определяются как первый момент времени и координата, в которых происходит обращение в ноль знаменателя соотношения (2.13). Если $F_{,\theta}(\theta) >0$  при всех допустимых  $\theta)$, то опрокидывания фронта не возникает. Учитывая, что концентрация частиц является всюду неотрицательной функцией, находим, что знаменатель в  (2.13) также является неотрицательным и, следовательно: $F_{,\theta}(\theta) \ge -\gamma t^2_*/2$. Возникновение же многозначности решения обязательно связано с изменением знака знаменателя в  (2.13) , что не имеет в рамках данной задачи физического смысла.

Используя теперь решение  (13) , получаем представление для интересующего нас интеграла:

$$\int\limits_{0}^d\theta(x,t)dx = \int\limits_{0}^d(F_{\theta}(\theta)+\gamma t^2/2)\theta(x,t) \theta_x dx=\int\limits_{\theta(0,t)}^{\theta(d,t)}(F_{\theta}\theta)+\gamma t^2/2)\theta(x,t) d\theta=$$
$$=Q(\theta(d,t))-Q(\theta(0,t))+\gamma t^2 \Big(\theta^2(d,0)-\theta^2(0,t)\Big)/4.$$
Здесь $Q(\theta) = \int F_{\theta}(\theta)\theta d\theta = F(\theta)\theta - \int F(\theta)d\theta$. Таким образом, уравнение для $x_0(t)$ теперь можно переписать в следующем виде:

$$\ddot{x}_0(t)=-\frac{q}{md}\phi_1(t)-\frac{\gamma}d}\Big[Q((\theta(d,t))-Q((\theta(0,t))+t^2\frac{\gamma}{4}\Big((\theta^2(d,t)-\theta^2(0,t)\Big)\Big]. \hspace{3cm}(14)$$

III.2.5. Пример 

В качестве такого начального распределения рассмотрим ситуацию, когда частицы сосредоточены вблизи одного из электродов с координатой $x=0$   с начальным распределением концентрации

$$n(x,0)=n_0\ch^{-2}(x-x_0(0)). \hspace{3cm} (16)$$
При рассмотрении таких распределений анализ уравнения для функции $x_0(t)$ становится сложным, поскольку приходится решать уравнение (14), вид правой части которого определяется неявно заданной функцией  $\theta$. Поэтому рассмотрим эволюцию начального распределения без граничного условия $\phi(d,t)=\phi_1(t)$, получая данные о функции $\phi_1(t)$ непосредственно из решения начальной задачи. Это позволяет полагать $x_0(t)=0$. Для простоты рассмотрим начальное распределение для скорости в том же виде, что и в предыдущей задаче, т.е. $v(x,0)=v_0={\rm const}$. В этом случае для функции $\theta$  получаем уравнение:

$$\theta = \frac{n_0}{k}\th\Big(k(x-x_0(t)-\gamma t^2 \theta/2)\Big).$$
Решение для концентрации частиц в этом случае имеет следующий вид:

$$n(x,t) = \frac{n_0}{\ch^2\Big(k(x-x_0(t)-\gamma t^2 \theta/2)\Big)+n_0\gamma t^2/2}.$$
На рис.(1),(2) и (3) приведены графики, описывающие поведение волны зарядовой плотности для начального условия (16) для параметров модели $q=-1,~n_0=1,~k=1,~\Gg=1,~v_0(0)=1,~x_0(t)=0$. Графики концентрации на рис.  (1) построены для последовательности моментов времени: кривая 1 -- $t=0$, кривые 2-11 для $t$, начиная с  $t=1$ через $\Delata t=0,25$, а графики изменения потенциала и скорости (рис. (2) и (3)) через   $\Delta t=0,5$ (кривые с номерами 2-8).

 

 

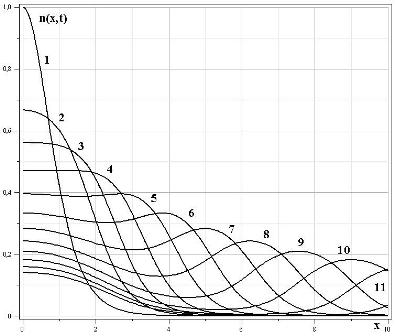
Рис. 1. Графики концентрации, отвечающие различным моментам времени

 

 

 

 

 

 

 

 

 

 

 

 

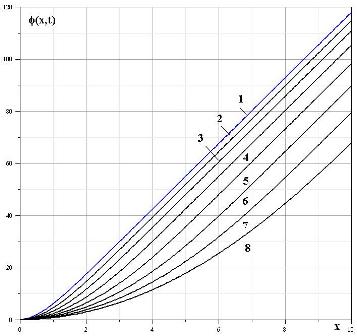
Рис. 2. Распределение потенциала, отвечающее различным моментам времени

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 3. Распределение скорости, в зависимости от времени

 

 

 

 

 

Анализ рисунка 1 показывает, что спустя некоторе после начала движения потока, в пространстве формируется второй максимум концентрации частиц и, как следствие, заряда. Этот максимум перемещается в пространстве в положительном направлении оси $x$ и представляет уединенную волну зарядовой плотности. При этом потенциал на аноде стремится к нулю. Фронт этой волны не опрокидывается.   

Список литетратуры

[1]  C. Child, Physical Review (Series I), 32, no. 5, 492 (1911).

[2]  I. Langmuir, Physical Review, 2, no. 6, 450 (1913).

[3]  Бурсиан В., Павлов В. Журнал Русского физ. общества, 55, N1-3, 71 (1923)

[4]  А.Е. Дубинов, И.А. Ефимова, И.Ю. Корнилова, С.К. Сайков, В.Д. Селемир. ФЭЧАЯ, 35, N2, 462 (2004)

[5]  В. И. Кузнецов, А. Я. Эндер. Физика плазмы, 36, № 3, 248–257 (2010): Физика плазмы, 36, № 3, с. 258–272 (2010)

[6]  Кузнецов В. И., Соловьев А. В., Эндер А. Я., ЖТФ, 64. Вып. 12, 9 (1994)

[7]  R.E. Caflisch1 and M.S. Rosin. arXiv:1110.2840v1 (2011)

[8]  M.S. Rosin, H. Sun. arXiv:1211.6794v1 (2012)

[9]  Журавлев В.М. Сб. Инновационные технологии. Под ред. проф. С.В. Булярского. Ульяновск. Изд. УлГУ, 2010 г., С. 77-93

[10]  Журавлев В.М., Никитин А.В. Нелинейный мир, 5, N 9. 603-611 (2007)

[11]  Журавлев В.М., ТМФ,  158, N 1, 58 (2009)  5, N 9, 603 (2007)

[12]  V. M. Zhuravlev and D.A.Zinov’ev. Physics of Wave Phenomena, 19, No. 4, 313–317 (2011)