Выяснилось, что силовой подход к решению уравнения невозмущенного кеплерова движения, скорее всего, возникал в период между 17 и 21 веком, но был отброшен...

Уравнение баланса сил при невозмущенном кеплеровом движении можно получить как двойным дифференцированием декартовых координат, так и дифференцированием по r уравнения сохранения энергии:

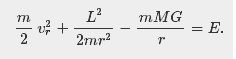
В обоих случаях мы приходим к уравнению:

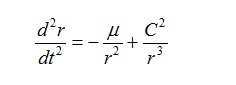
 Это уравнение описывает невозмущенное кеплерово движение, которое мало кому интересно. Однако это же уравнение позволяет вводить возмущающие силы: в виде постоянной добавки или же, рассматривая постоянные, фигурирующие в уравнении не как постоянные, а как функции времени. 

Пример. Введение добавочной силы +0.1С²/r³  заставляет эллипс прецессировать, что эквиваленто добавке соответствующей потенциальной энергии

в уравнение энергий.

Центр Земли, вокруг которого движется спутник, тоже движется ускоренно, создавая добавку в наше основное уравнение в инерционной части. Это легко учесть  и посчитать изменение параметров орбиты.

Гравитационное поле Земли неоднородно или не имеет сферической симметрии? Это можно учесть в гравитационной части уравнения. И опять же посчитать изменение параметров возмущенной орбиты. 

Этот подход максимально универсален, прост и понятен. НО. Уравнение в указанной мной форме баланса сил нигде не встерчается. Почему?

P.S.

Все авторы учебников физики, за исключением, пожалуй, Л.Д. Ландау выписывают формулу для периода кеплерова движения через большую полуось. От этого может возникнуть впечатление, что периоды обращения спутников с одинаковыми большими полуосями равны! Это не так.

Да и у Ландау в формула с изюминкой.

Можно подумать, что  период обращения зависит от массы!

Настоящая формула для периода эллиптического кеплерова движения выглядит так: