Сегодня я расскажу о задаче, с которой столкнулся в книге П. Маковецкого «Смотри в корень» http://n-t.ru/ri/mk/sk035.htm.

            Там, в частности, он пишет, что «Спутник-гантель тоже будет колебаться (с периодом, близким по величине к периоду обращения вокруг Земли и почти не зависящим от размеров и формы гантели) вокруг прямой, соединяющей его с центром Земли.»

            Я решил проверить это утверждение. Для этого мне потребовалось научиться записывать уравнения Лагранжа первого рода – дифференциальные уравнения движения механической системы в декартовых координатах, содержащие множители Лагранжа.

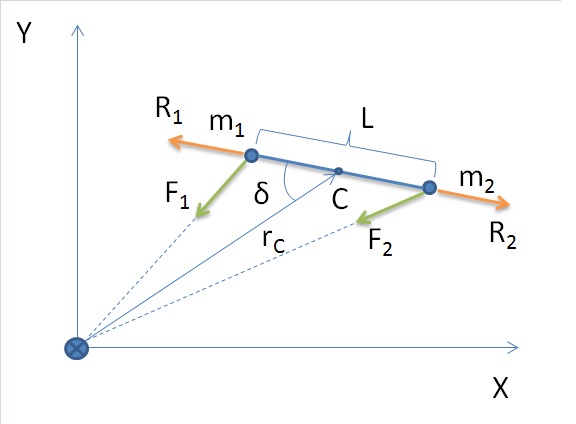
            Идеализированный спутник-гантель представляет собой две точечные массы, соединенные невесомым стержнем (связью). На каждую из этих масс действуют две силы – сила тяжести и сила реакции связи (Рис. 1).

           Запишем второй закон Ньютона для нашей системы:

           Уравнение связи накладывает ограничение на взаимное перемещение половинок гантели:

           Проекции реакций связи на координатные оси пропорциональны частным производным от функции связи по соответствующим координатам. Коэффициенты пропорциональности принято называть множителями Лагранжа.

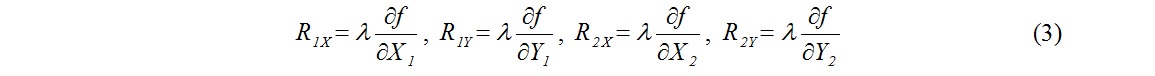 Допустим, массы половинок гантели равны: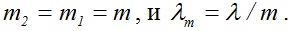

            Тогда система векторных уравнений (1) в декартовых координатах будет   выглядеть следующим образом:

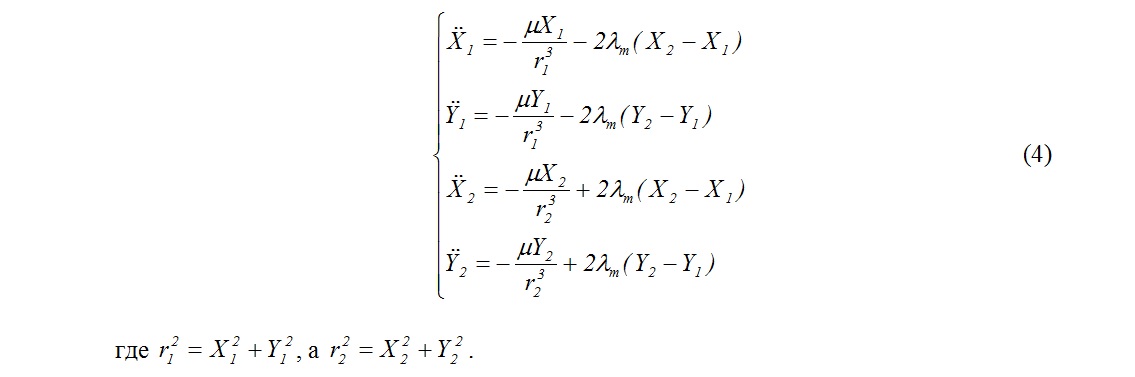
            Здесь есть одна тонкость с определением множителей Лагранжа. Их мы найдем с помощью двойного дифференцирование уравнения связи. После первого дифференцирования (2) получим

            После второго дифференцирования -

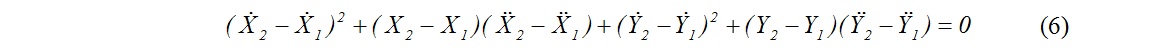
            В то же время (см. (4))

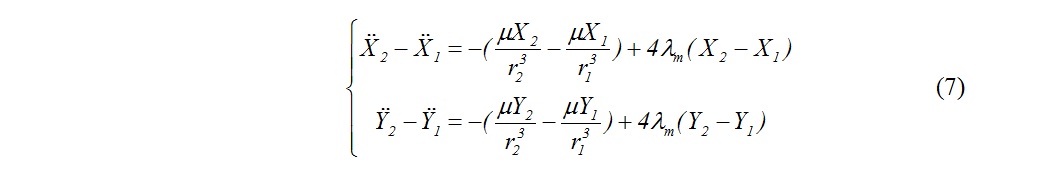
             Умножая левую и правую части (7) на разности координат и прибавляя разности скоростей, приходим к выражению (8):

             Складывая первую и вторую строчки (8), получаем согласно (6) слева 0. И, вводя обозначения

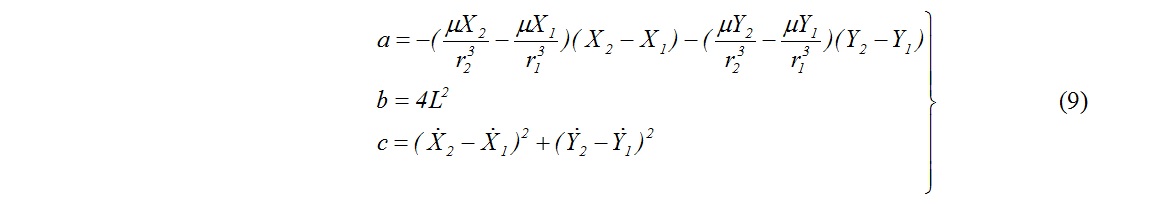
получаем

             Пусть в начале все точки гантели расположены горизонтально по оси X и имеют одинаковую скорость, равную круговой для центра масс С. Решив систему уравнений (4) найдем координаты и скорости половинок гантели.

            По теореме косинусов угол между направлением на центр Земли и осью гантели можно определить из следующего отношения:

             где X_c, Y_c–  координаты центра масс, которые равны:

           Однако здесь нас ждет еще один тонкий момент – знак угла. Если гантель закручивается по часовой стрелке, угол будем считать положительным. В зависимости от направления вектора

L x r_c определим знак угла "дельта" с помощью функции

             Теперь можно записать выражение для зависимости угла наклона нашей гантели к «местной вертикали»:

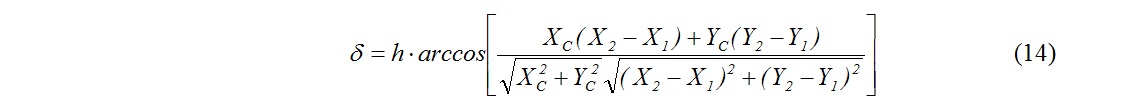
Изменение угла  "дельта" со временем для высоты круговой орбиты 200 км и длины гантели 10 м можно видеть на Рис. 2. Здесь  фи(t) это косинус аномалии центра масс.

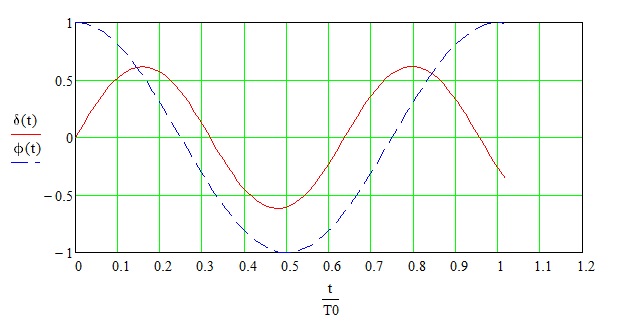
Рис. 2.

            Период обращения центра масс составляет около 88,5 мин. Видно, что период колебания гантели примерно на треть меньше! Это неожиданный результат.

            Однако, если мы обратимся к Белецкому В.В. [1], то узнаем вот что:

            Колебания гантели, оказывается, не так уж малы – амплитуда их равна примерно 35°. Поэтому их период чуть больше, указанного Белецким.

            Теперь, когда уравнения движения нашей системы известны, открывается простор для исследований. Интересно, какое влияние на параметры движения оказывает длина связи? Какие напряжения возникают в ней? Как будет происходить движение, если массы на концах стержня будут разными? Как поведет себя система на эллиптической орбите?

Источники информации.

1.     Белецкий В. В.  Движение искусственного спутника Земли относительно центра масс. — М.: Наука, 1965. — 416 с.