Динамическое равновесие звезд

Работа является несколько измененным вариантом статьи Журавлев В.М. Модели динамического равновесия астрофизических объектов. ЖЭТФ, 2022, т. 162, N 6, с. 850-877

1. Статическое и динамическое равновесие

Звезды представляют собой газовые или точнее плазменные шары, находящиеся в равновесии. Равновесие таких систем определяется по факту того, что их размеры и температура  мало изменяются со временем. Такое равновеси принято называть статическим. Есть звезды, которые меняют свой радиус периодически в заметных пределах. Такие колебания радиуса указывают на то, что равновесие звезд носит динамический характер. К звездам такого типа, в первую очередь, относятся цефеиды. Цефеиды - это класс звезд, как правило, красных гигантов, светимость (количество энергии излучаемое всей поверхностью звнзды в единицу времени) которых меняется с периодом от нескольких суток до месяцев. Между светимостью свезд и периодом осцилляций или пульсаций имеется универсальная связь - так называемая диаграмма период-светимость. Важность этой диаграммы состоит в том, что с ее помощью можно по периоду колебаний установить светимость звезды, а по светимости можно узнать расстояние до этой зыезды. Для удаленных звезд это наиболее эффективный способ определить расстояние до них. Одним из наиболее впечатляющих примеров использования цефеид в качестве инструсента определения расстояния до астрономических объектов, в состав которых входит цефеида, является работа  в 1923 году Эдвина Хаббла по установлению расстония до туманности Андромеда. На пути к этой туманности Э.Хаббл обнаружил цефеиду. Период ее пульсаций оказался таким, что измеренная по нему светимость указала на то, что звезда должна располагаться от нас на расстоянии более чем $1.5\cdot 10^6$ св. лет от Земли. С этого момента стало ясно, что множество туманностей, которые, как считалось, относятся к нашей звездной системе, на самом деле являются отдельными звездными островами, которые сейчас мы называем галактиками. В реальности расстояние до галактики Андромеда, ближайшей к нам большой галактике оценивается в $2.5\cdot 10^6$ св. лет. Множество других галактик, как сейчас изветно лежат на гораздо больших расстояниях от нашей галактики Млечный путь (Галактика). 

Причиной статического и динамического равновесия звезд и других астрофизических объектов является баланс силы тяготения и Архимеда в них. В случае динамического равновесия баланс сил тяготения и Архимеда несколько  нарушается. Вопросы, относящиеся к проблемам того, как происходит это нарушение и каковы его следствия, являются основной целью данной статьи.

1. Краткая теория Лейна-Эмдена звездных политроп

Одной из первых теорий строения звезд явилась теория или модель Лейна-Эмдена [18,19], созданная в конце IX начале XX веков. Авторы вложили в основу теории следующие упрощающие предположения. Во-первых, звезды предполагались строго сферическими объектами, состоящими из идеального газа в виде атомов. Во-вторых, состояние газа предполагалось политропным, т.е. давление $p$ в любой точке газа опредедяется целиком его плотностью $\rho$ в соответствии с соотношением: $$p=p(\rho)$$. В третьих, звезда находится в строгом статическом равновесии. Поэтому ее параметры не меняются  со временем и, более того, ни каких потоков перемещения газа внутри звезды нет. 

      Из этих трех предположений можно сделать следующие выводы. Во-первых, раз газ идеальный и состоит из атомов (в основном из водорода и гелия), то уравнение состояния газа можно уточнить и записать в таком виде: $$\label{Eqp} p=K_0\rho^{\gamma}.\tag{1.1}$$ В этой формуле $\gamma$ - показатель адиабаты газа, который полностью определяется типом атомов, из которых состоит этот газ. Коэффицент $K_0$ связан с энтропиней газа. Формула для $K_0$ будет позже уточнена. Из молекулярной физики величина $\gamma$ находится из формулы: $$\gamma=\frac{i+2}{i},$$ где $i$ - число степеней свободы одного структурного  элемента газа. В звездах, обычно, структурные элементы газа представляют собой  отдельные атомы вещества, не связанные между собой. Для такого газа не зависимо от химического  элемента, к которому относятся его атомы,  $\gamma=5/3$, поскольку такие атомы  могут двигаться только в терех пространственных направлениях, т.е. для них $n=3$. В некоторых случаях величина $\gamma$ определяется из других соображений. Например, в случае ультрарелятивистских белых карликов, свойства вещества звезды определяются квантовыми законами и для этих звезд $\gamma=4/3$.

Во-вторых, исходя из сделанных предположений можно записать два уравнения, которые определяют математически условие статического равновесия газа. Первое уравнение - это равенство нулю всех сил, действующих на частицу в газе. С одно стороны, это сила тяготения $F_g$, а сдругой - сила Архимеда $F_A$. Объемную силу тяготения, т.е. приложенную к еденице объема, можно записать в таком виде: $$\label{EqFg} F_g=-\rho\frac{\partial}{\partial r}\phi(r) \tag{1.2}.$$ А объемную силу Архимеда в таком: $$\label{EqFA} F_A=-\frac{\partial}{\partial r}p(\rho). \tag{1.3}$$ В формулу для силы тяготения $F_g$ входит функция $\phi(r)$ - потенциал поля тяготения, который удовлетворяет уравнению Пуассона:  $$\label{EqPs} \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial \phi}{\partial r}\right)=4\pi G\rho. \tag{1.4}$$ Здесь и далее $G$ - постоянная тяготения Ньютона. Поскольку равновесие считается точным, то должно выполняться уравнение баланса сил: $$\label{EqF0} F_g+F_A=-\rho\frac{\partial}{\partial r}\phi-\frac{\partial}{\partial r}p=0. \tag{1.5}$$ Отсюда находим, что должно выполняться равенство: $$\label{Eqpphi}\frac{\partial}{\partial r}\phi=-\frac{1}{\rho}\frac{\partial}{\partial r}p(\rho). \tag{1.6}$$ Подставляя это соотношение в уравнение (\ref{EqPs}), приходим к уравнению Лейна-Эмдена: $$\label{EqLEmrho} \frac{1}{r^2}\frac{\partial}{\partial r}\left(\frac{r^2}{\rho}\frac{\partial p(\rho)}{\partial r}\right)+4\pi G\rho=0. \tag{1.7}$$ Подставляя в это уравнение соотношение (\ref{Eqp}) и делая замену $\rho=\rho_0\theta^n$, где $n=1/(\gamma-1)$ - показатель политропы, приходим к такой форме этого уравнения: $$\frac{1}{r^2}\frac{\partial}{\partial r}\left(\frac{K_0\gamma\rho_0^{\gamma-1}}{\gamma-1}r^2\frac{\partial \theta}{\partial r}\right)+4\pi G\rho_0\theta^n=0.$$ В этом уравнении $\rho_0$ - постоянная размерности плотности массы, а $\theta(r)$ - безразмерная функция, совпадающая с температурой с точностью до постоянного множителя.  Последнее уравнение в безразмерном виде можно записать так: $$\label{EqLEm}\frac{1}{\xi^2}\frac{\partial}{\partial \xi}\left(\xi^2\frac{\partial \theta}{\partial \xi}\right)+\theta^n=0. \tag{1.8}$$ Здесь $\xi=r/r_0$ - безразмерная координата, где $$r_0=\sqrt{\frac{4\pi G(\gamma-1)}{\gamma K_0 \rho_0^{\gamma-2}}}$$ - масштабный множитель радиуса.

Для решения уравнения (\ref{EqLEm}) необходимо задать граничные условия. Эти граничные условия являются следствием двух простых условий. Первое из них состоит в выборе не определенного пока параметра $\rho_0$ в виде значения плотности в центре звезды: $$\rho_0=\rho(0).$$ В этом случае первое граничное условие для функции $\theta(\xi)$ будет выглядеть так: $$\label{BC1}\theta(0)=1. \tag{1.9}$$ Второе граничное условие получается из требования, что в центре звезды плотность и другие параметры среды не обращаются в бесконечность. Дело в том, что среди решений уравнения (\ref{EqLEm}) есть сингулряные решения, обращающиеся в бесконечность в центре звезды. Для исключения таких решений, опуская простые, но громоздкие расчеты (см. например, [1,4]), находим второе граничное условие: $$\label{BC2} \left.\frac{\partial \theta}{\partial \xi}\right|_{\xi=0}=0. \tag{1.10}$$  Уравнение (\ref{EqLEm}) вместе с граничными условиями (\ref{BC1})-(\ref{BC2}) содержит единственный параметр $n$ - показатель политропы. Следовательно, строение звезд в таком упрощенном виде определяется исключительно типом структурных элементов газа (плазмы), из которых она  состоит. Поэтому графики изменения плотности и температуры для различных звезд с одинаковым значением $\gamma$ будут отличаться лишь плотностью в центре звезды $\rho_0$ и, возможно, значением постоянной $K_0$, определяющей энтропию в звезде.
       На рис. 1.1 представлены графики $\theta(\xi)$ для неcкольких значений $\gamma$.

Рис. 1.1. Распределение безразмерной температуры $\theta$ среды по радиусу $\xi$ для нескольких значений $\gamma$

Как видно из графиков на рис. 1 все кривые, кроме кривой с $\gamma=6/5$, пересекают ось абсциис в некотрой точке $\xi_0$. Обычно это интерпретируется как существование реального радиуса звезды $R_*=r_0 \xi_0$, поскольку решение при $\xi > \xi_0$ оказывается отрицательным или комплексным. Для $\gamma\le 6/5$ пересечение с осью абсцисс отсутствует, что интерпретируется как не возможность существования равновесного состояния звезды.

Для некоторых значений $\gamma$ можно получить точные решения. Такие точные решения существуют для значений $\gamma=\infty$, $\gamma=2$ и $\gamma=6/5$. Для $\gamma=\infty$ показатель политропы равен $n=0$. Такое состояние считают несжимаемой жидкостью. (см. [1,4]) В этом случае уравнение (\ref{EqLEm}) интегрируется прямым образом, что с учетом граничных условий дает такое решение: $$\theta(\xi)=1-\frac{\xi^2}{6}.$$  Значение безразмерного радиуса звезды $\xi_0$ для этого варианта равно $\xi_0=\sqrt{6}$.
      В случае $\gamma=2$ показатель политропы равен $n=1$ и уравнение (\ref{EqLEm}) принимает такой вид: $$\label{EqLEmn1}\frac{1}{\xi^2}\frac{\partial}{\partial \xi}\left(\xi^2\frac{\partial \theta}{\partial \xi}\right)+\theta=0.\tag{1.11}$$ Для функции $q=\xi\theta(\xi)$ это уравнение принимает вид уравнения гармонического осциллятора: $$\frac{\partial^2 q}{\partial \xi^2}+q=0$$ Решением этого уравнения с учетом граничных условий является функция $q=\sin(\xi)$. Отсюда решением уравнения для $\theta(\xi)$ (см. [1,4]) является функция: $$\label{SolLEmn1}\theta = \frac{\sin(\xi)}{\xi}.\tag{1.12}$$ В этом случае $\xi_0=\pi.$ Хотя вариант $\gamma=2\ (n=1)$ с точки зрения практического приложения не особенно ценен, он дает представление о том, что участки среды с равновесным значением плотности и температуры могут существовать не только вблизи центра звезды. На рис. 1.2 приведен график измеения $\theta(\xi)$ для $\gamma=2$ и $\gamma=4/3$. Вариант $\gamma=4/3$ важен, поскольку соответствует ультрарелятивистскому веществу в белых карликах предельно большой массы, вычисленной Чадрасекаром. 
 

Рис. 1.2. Распределение безразмерной температуры для $\gamma=2$ и $\gamma=4/3$. Красным выделены области с отрицательными значениями безразмерной температуры, а синим - с положительнами

     Для $\gamma=6/5\  (n=5)$ точное решение получить более сложно. Это решение имеет такой вид: $$\label{SolLEmn5} \theta = \frac{1}{\sqrt{1+\xi^2/3}}.\tag{1.13}$$ В этом случае $\xi_0=\infty$

Варианты с $\gamma=2 (n=1)$ и $\gamma=4/3\ (n=3)$ показывают , что в решениях могут существовать области  при больших радиусах, чем $\xi_0$, в которых существует равновесие среды. Эти области выделены синим цветом.  Чему в реальности соответствуют такие области равновесия, не ясно из теории Лейна-Эмдена. Из общих соображений ясно, что вне звезды находится газ, который также должен находится в равновесии, псокольку звезда не меняет своих размеров и свойств. Тем не менее, в некоторых областях равновесие может существовать, а в других - нет. Объяснению этой ситуации и будет посвящена часть данной работы.  

2. Уравнения динамики газа для вращающейся звезды

Исходными уравнениями для описания того, как устроены звезды являются уравнения динамики газа или плазмы, из которых они состоят, включая уравнение сохранения массы.  Уравнения для поля тяготения в форме уравнения Пуассона для потенциала $\phi$, а также уравнения состояния газа. Уравнение Пуассона (\ref{EqPs}), уравнение состояния (\ref{Eqp}), а также редуцированное уравнение динамика газа  в форме уравнения равенства нулю суммы силы тяготения и силы Архимеда (\ref{EqF0}) уже были введены ранее. Но для описания движущейся среды необходимо эту систему уравнений расширить и дополнить. Поскольку далее мы будем рассматривать звезды и другие объекты, имеющие собственное вращение, то для описания потока газа по отношению к системе отсчета, связанной с центром звезды необходимо включить уравнения для всех трех компонент скорости ${\bf U}=(u,v,w)$ потока. Выберем в качестве системы координат цилиндрическую с осью $z$, направленной вдоль оси вращения звезды. В этом случае компонента $u(r,z,\varphi,t)$ будет направлена вдоль радиального направления цилиндрической системы координат (перпендикулярной оси вращения). Компонента  $v(r,z,\varphi,t)$ будет описывать зональную составляющую потока, которая описывает вращение вокруг оси в данной точке пространства. Компонента $w(r,z,\varphi,t)$ - скорость потока вдоль оси вращения. Будем предполагать, что все компоненты потока и праметры среды такие как плотность массы $\rho$ И температура $T$ не зависят от азимутального угла $\varphi$, т.е будем предполагать, что звезда обладает цилиндрической симметрией. Поэтому: $$u=u(r,z,t),~v=v(r,z,t),~w=w(r,z,t),~\rho=\rho(r,z,t),~...$$

В результате совокупность уравнений динамики газа в цилиндрической системе координат будет иметь такой вид: $$u_t+uu_r+wu_z-\frac{v^2}{r}=-\phi_r - \frac{1}{\rho}p_r,$$$$\label{EqEulier}w_t+uw_r+ww_z=-\phi_z - \frac{1}{\rho}p_z, \tag{2.1}$$$$v_t+uv_r+wv_z+\frac{vu}{r}=0;$$$$\label{Eqrho}\rho_t+\frac{1}{r}\frac{\partial}{\partial r}\Big(ru\rho\Big)+\frac{\partial}{\partial z}\Big(w\rho\Big)=0; \tag{2.2}$$$$\label{EqPsC}\frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial \phi}{\partial r}\right)+\frac{\partial^2}{\partial z^2}\phi=4\pi G \rho. \tag{2.3}$$
Здесь и далее для сокращения записи введены обозначения: $$f_r=\frac{\partial f}{\partial r},~~f_z=\frac{\partial f}{\partial z},~~f_t=\frac{\partial f}{\partial t},~~f_{zz}=\frac{\partial^2 f}{\partial z^2},~~f_{rz}=\frac{\partial^2 f}{\partial z\partial r},\ldots$$
К этой системе уравнений необходимо добавить уравнение состояния, которое будет выведено далее. Это уравнение будет отличаться от уравнения (\ref{Eqp}) множителем, учитывающим тепловой поток в звезде.

2.1. Метод гидродинамических маркеров

Для анализа системы уравнений (\ref{EqEulier})-(\ref{EqPsC}) применим метод гидродинамических маркеров [20,21]. Метод гидродинамических маркеров опирается на предположение, что газ можно рассматривать как совокупность отдельных частиц - атомов, у которых есть некоторые физические свойства, которые не меняются при движении частиц в газе. Такие свойства и называются маркерами. В гидродинамике часто в качестве маркеров используют координаты точек среды в некоторый начальный момент времени [Lamb,KK]. Двигаясь в пространстве частицы сохраняют начальные координаты своего положения. Для описания среды, имеющей цилиндрическую симметрию достаточно  ввести два маркера $e_1(r,z,t)$ и $e_2(r,z,t)$, которые будут далее называть маркерными полями. По определению маркеры удовлетворяют уравнениям переноса: $$\label{Eqe12} \frac{de^a}{dt}=e^{a}_t+ue^a_r+we^a_z=0,~~a=1,2. \tag{2.4}$$

2.1.1.  Уравнение сохранения числа частиц и уравнение сохранения массы

Введем для удобства записи обозначение: $x^1=r,~x^2=z$, и вектороное поле ${\bf W}=(u,w)$. Тогда следстивием уравнения (\ref{Eqe12}) является закон, аналогичный закону сохранения массы в дифференицальной форме (уравнение неразрывности). Продифференцируем уравнения (\ref{Eqe12}) по $x^{\alpha}$ и умножим полученное выражение на элементы  $\partial x^{\alpha}/\partial e^a$ матрицы, обратной матрице Якоби $\hat{J}$ отображения $x^{\alpha}->e^a$: $$\label{DefmJ}\hat{J}=\left(\frac{\partial e^a}{\partial x^{\alpha}}\right).\tag{2.5}$$  После этого свернем результат по индексам $\alpha$ и $a$: $$\frac{\partial x^{\alpha}}{\partial e^a}\left(\frac{\partial }{\partial t}\frac{\partial e^a}{\partial x^{\alpha}}+\frac{\partial }{\partial x^{\alpha}}\left(W^{\beta}\frac{\partial e^a}{\partial x^{\beta}}\right)\right)=0.$$ Здесь и далее предполагается суммирование по повторяющемуся индексу. Учитывая свойства определителя матрицы, окончально, последнее соотношение можно записать в такой форме: $$\label{EqCJ}\frac{\partial |J|}{\partial t}+\frac{\partial }{\partial r}\Big(u|J|\Big)+\frac{\partial }{\partial z}\Big(w|J|\Big)=0,\tag{2.6}$$ где: $$\label{DefJ} J=\det\hat{J}. \tag{2.7}$$
    Соотношение (\ref{EqCJ}) представляет собой закон сохранения плотности маркеров, которую можно отждествить с плотностью массы среды, полагая: $$\label{DefrhoJ} \rho = M_0\frac{ |J|}{r},\tag{2.8}$$ где $M_0$ - некоторая постоянаая размерности массы. В этом случае уравнение (\ref{EqCJ}) в точности переходит в уравнение (\ref{Eqrho}). Соотношение (\ref{DefrhoJ}) означает, что масса всех частиц среды одинакова, а ее плотность определяется плотностью частиц, которая равна $|J|$.

2.1.2.  Маркеры и гравитационное поле

     Следующим важным элементом метода маркеров является возможность описать гравитационное поле в терминах маркерных полей $e^a(r,z,t)$ [36,37,38,39,40,41]. Для этого рассмотрим формальное тождество: $$\label{EquivE} \frac{\partial e^a}{\partial e^a}=2, \tag{2.9}$$ Переходя в этом тождестве от маркерных координат $e^a$ в пространстве маркеров ${\cal E}$ к координатам  $r,z$ в физическом пространстве, получаем уравнение следующего вида: $$\label{EqJGP} \frac{\partial }{\partial x^{\alpha}}\left(|J|e^b\frac{\partial x^{\alpha}}{\partial e^b}\right)=2|J| . \tag{2.10}$$ Используя соотношение (\ref{DefrhoJ}), тождество (\ref{EqJGP}) можно записать в таком виде: $$\label{EqEP}\frac{1}{r}\frac{\partial}{\partial r}\left(rK^1\rho\right)+\frac{\partial}{\partial z}\Big(K^2\rho\Big)=4\pi G\rho,\tag{2.11}$$ где: $$\label{DefK} K^1=2\pi G e^b\frac{\partial r}{\partial e^b},\ \ K^2 =2\pi G e^b\frac{\partial z}{\partial e^b}\tag{2.12}$$  - компоненты вспомогательного вектора. Если теперь отождествить вектор ${\bf g}$ с компонентами: $$\label{Defg} g^1=2\pi G e^b\frac{\partial r}{\partial e^b}\rho+\Phi_r,\ \ g^2 =2\pi G e^b\frac{\partial z}{\partial e^b}\rho+\Phi_z \tag{2.13}$$ с компонентами вектора ускорения свободного падения, то уравнение (\ref{EqEP}) превратися в уравнение Пуассона:   $$\label{EqPouis}\frac{1}{r}\frac{\partial}{\partial r}\Big(rg^1\Big)+\frac{\partial}{\partial z}g^2=4\pi G\rho,\tag{2.14}$$ для поля тяготения. В последних соотношениях $\Phi$ - вспомогательный потенциал, необходимый для удовлетворения граничным условиям и удовлетворяющий уравнению: $$\label{EqPhi}\frac{1}{r}\frac{\partial}{\partial r}\left(r\Phi_r\right)+\frac{\partial}{\partial z}\Big(\Phi_z\Big)=0,\tag{2.15}$$
     Для вычисления компонент вектора ${\bf K}$ воспользуемся тем, что производные $\partial x^{\alpha}/\partial e^a$ являются элементами матрицы, обратной матрице Якоби ${\hat J}$ (\ref{DefmJ}). Исходя из этого, находим: $$|J|\frac{\partial r}{\partial e^1} = \frac{\partial e^2}{\partial z},~~|J|\frac{\partial r}{\partial e^2} = -\frac{\partial e^2}{\partial r},$$ $$|J|\frac{\partial z}{\partial e^1} = -\frac{\partial e^1}{\partial z},~~|J|\frac{\partial z}{\partial e^2} = \frac{\partial e^1}{\partial r}.$$ Отсюда: $$\label{DefKe} |J|K^1 =\frac{\partial e^2}{\partial z}e^1-\frac{\partial e^1}{\partial z}e^2,~~|J|K^2=\frac{\partial e^1}{\partial r}e^2-\frac{\partial e^2}{\partial r}e^1.\tag{2.16}$$ Теперь первые два уравнения системы (\ref{EqEulier}) можно переписать в обновленной форме: $$u_t + uu_r + wu_z -\frac{v^2}{r} = -\frac{1}{\rho}p_r -\frac{2\pi G M_0}{r}|J|K^1+\Phi_r,$$ $$\label{Equ1}w_t + uw_r + ww_z = -\frac{1}{\rho}p_z -\frac{2\pi G M_0}{r}|J|K^2+\Phi_z.\tag{2.17}$$

2.1.3.  Маркеры и зональная составляющая потока

Следующим важным соотношением, связывающим физические парамтры среды и ее динамики с маркерами, является закон дифференицальный сохранения момента импульса потока. Этот закон следует из третьего уравнения системы (\ref{EqEulier}), которое можно перемисать в таком виде:
$$ \frac{\partial }{\partial t}\Big(rv\Big)+u\frac{\partial }{\partial r}\Big(rv\Big)+w\frac{\partial }{\partial z}\Big(rv\Big)=0.\tag{2.18}$$ Отсюда следует, что функция $V=rv$ является функцией маркеров: $$\label{DefV}V=rv=V(e^1,e^2). \tag{2.19}$$ Отсюда следует, что зональную компоненту скорости можно представить так: $$\label{Defv} v =\frac{V(e^1,e^2)}{r}. \tag{2.20}$$

2.2. Гидродинамический поток Хаббла и автомодельные переменные

Для выделения главных особенностей эволюции газодинамических структур используется идея представления параметров среды в виде функций от автомодельных переменных [5,2,6,13,14,15,16,17]. В случае потока с цилиндрической симметрией введем две автомодельные переменные $\xi=r/a(t)$ и $\zeta=z/b(t)$. Функции $a(t)$ и $b(t)$ обычно называют масштабными факторами, которые являются аналогом масштабных факторов в задачах космологии [5,2,6]. В таком подходе предполагается, что эволюция структур, например, звезд, сводится к растяжению или сжатию их пространственной структуры при неизменной ее формы в автомодельных переменных. Такое предположение приводит к достаточно жестким ограничениям на общую форму гидродинамического потока, которые означают, что маркеры $e^{j}(r,z,t),~j=1,2$ можно записать в следующей общей форме: $$\label{Defea}e^{j} = \tau_j(t){\cal E}^{j}(\xi,\zeta),~~j=1,2,\tag{2.21}$$ где $\tau_{j}(t)$ - некоторые функции времени, а ${\cal E}^{j}(\xi,\zeta)$ - функции  автомодельных переменных. Аналогичное представление делается при анализе автомодельной динамики быстрой эволюции звезд (взрыве или коллапсе [5,2,6,13,14,15,16,17]). В этом случае находим:
$$\label{DefrhoR}\rho =\frac{M_0\tau_1(t)\tau_2(t)}{a(t)^2b(t)}{\cal R}(\xi,\zeta),\tag{2.22}$$ где: $$\label{DefcRJ}{\cal R} = \frac{|{\cal J}(\xi,\zeta)|}{\xi},~~~{\cal J}=\det\left|\begin{array}{cc}
                  {\cal E}^1_{\xi} & {\cal E}^1_{\zeta}\\
                  {\cal E}^2_{\xi} & {\cal E}^2_{\zeta}
              \end{array}\right|.\tag{2.23}$$
Эту функцию в дальнейшем будем называть коэффициентом плотности. Подставляя (\ref{Defea}) в уравнения переноса маркеров (\ref{Eqe12}), приходим к следующим соотношениям: $$\Theta_j{\cal E}^{j}+\frac{{\cal E}^{j}_{\xi}}{a(t)}\Big(u-H(t)r\Big)+\frac{{\cal E}^{j}_{\zeta}}{b(t)}\Big(w - F(t) z\Big)=0,~~\label{Eqee}j=1,2.\tag{2.24}$$ Здесь $$\Theta_j=\frac{\dot{\tau}_{j}}{\tau_{j}},~~j=1,2;~~~ H = \frac{\dot{a}}{a},~~F= \frac{\dot{b}}{b}.$$ Функции $H=H(t)$ и $F=F(t)$ называются в космологии параметрами Хаббла.
     Общее решение системы (\ref{Eqee}) относительно компонентов $u(r,z,t)$ и $w(r,z,t)$ скорости потока имеют такой вид: $$\label{Soluv}u = H(t) r + a(t)\frac{\Theta_2 {\cal E}^2{\cal E}^1_{\zeta}-\Theta_1 {\cal E}^1{\cal E}^2_{\zeta}}{{\cal J}},\tag{2.25}$$ $$w = F(t) z + b(t)\frac{\Theta_1 {\cal E}^1{\cal E}^2_{\xi}-\Theta_2 {\cal E}^2{\cal E}^1_{\xi}}{{\cal J}}.$$ Если рассматривать ситуацию, когда $\dot{\Theta}_{j}=0,~j=1,2$, то система (\ref{Eqee}) оказывается вырожденной относительно $u$ и $v$. В силу требования независимости ${\cal E}^1(\xi,\zeta)$ и ${\cal E}^2(\xi,\zeta)$ друг относительно друга (иначе плотность обращается в ноль), единственным решением системы (\ref{Eqee}) относительно $u$ и $w$ в этом случае является анизотропный поток Хаббла: $$\label{EqHab} u= H(t)r = a(t)H(t) \xi,~~ w = F(t)z = b(t)F(t)\zeta.\tag{2.26}$$ Для такого выбора компонентов потока имеем: $$\label{EqArz} u_t+uu_r+wu_z= a(\dot{H}+H^2)\xi,\tag{2.27}$$ $$ w_t+uw_r+ww_z= b(\dot{F}+F^2)\zeta.$$
     Ранее сферически-симметричные модели космологических течений с потоком Хаббла в рамках классической механики Ньютона рассматривались в работах [5,27,28]. Следует отметить, что стандартным подходом к выбору автомодельных переменных (см. [5,2,6]) является явное определение функциональной зависимости $a=a(t)$ в виде некоторой степенной функции. В этом случае появляется возможность более общего выбора пространственного распределения скорости потока в зависимости от автомодельной переменной $\xi$, но ограничивается форма автомодельной эволюции газа со временем. В противоположность этому в случае выбора скорости потока в форме (\ref{EqHab}) можно получить модели с более ограниченным по форме пространственным распределением параметров газовой среды, эволюция которой со временем описывается более общей системой уравнений [12]. Ограничения пространственного распределения параметров среды в случае выбора закона Хаббла сводятся к тому, что автомодельное уравнения для плотности или температуры оказываются некоторой модификацией уравнения Лейна\,--\,Эмдена [12]. Именно этот вариант и будет рассматриваться далее в данной работе.

3. Термодинамические условия в среде

В данной работе будет рассматриваться модель  самогравитирующей среды в форме идеального газа с  уравнением состояния Менделеева-Клапейрона: $$\label{EqPMK} p= \frac{{\cal A}}{\mu_g}\rho T,\tag{3.1}$$где ${\cal A}$ - универсальная газовая постоянная, а $\mu_g$ - молярная масса газа. На термодинамические процессы в газе будут накладываться определенные ограничения. Эти ограничения связаны с тем, как происходят изменения локальной энтропии $s(r,z,t)$ со временем. Такие ограничения возникают как условия автомодельности самогравитирующей  системы, обладающей автомодельным потоком Хаббла (\ref{EqHab}).
 
3.1. Автомодельные режимы распределения энтропии

Согласно первому закону термодинамики, в каждой точке пространства для идеального газа приращение энтропии [2] можно представить в следующем виде: $$ds/c_v = d\ln\left(T\rho^{1-\gamma}\right).$$ Здесь $c_v$ - молярная теплоемкость при постоянном объеме, а $\gamma$ - показатель адиабаты. Отсюда следует: $$\label{DefTs} T = Q_0 \rho^{\gamma-1} e^{s/c_v},\tag{3.2}$$ где $Q_0$ - некоторая постоянная, характеризующая состояние газа в некоторой фиксированной точке пространства. Если локальная энтропия постоянна в пространстве и времени: $s={\rm const}$, то процесс расширения или сжатия газа будет ``глобально'' адиабатическим. Локально адиабатический процесс соответствует условию, когда энтропия не меняется вдоль линий переноса газа. В этом случае для $s$ имеем уравнение переноса: $$\label{Eqs0} \frac{ds}{dt}\equiv s_t+us_r+ws_z=0.\tag{3.3}$$ В этом случае энтропия является некоторой функцией гидродинамических маркеров: $s=s(e^1,e^2)=S(\xi,\zeta)$. Такие процессы характерны для процессов взрыва звезд, расширения звездных оболочек [2,6] и процессов космологического расширения, когда диффузионной теплопередачей можно пренебречь.
    Кроме таких процессов в дальнейшем будут рассматриваться и квазиадиабатические процессы, для которых энтропия будет явно зависеть от времени по следующему закону: $$\label{DefSt1} s = s_a(\xi,\zeta)+s_0(t).\tag{3.4}$$ Здесь $s_a(\xi,\zeta)$ - некоторая функция автомодельных переменных, а $s_0(t)$ - функция времени, характеризующая поступление тепла в систему. Такие процессы эквивалентны уравнению для $s$ следующего вида: $$\frac{ds}{dt} = \dot{s}_0,$$ что соответствует однородному по пространству оттоку или притоку тепла в систему  в зависимости от знака функции $\dot{s}_0$. Эти режимы теплообмена важны при описании моделей динамики газа с автомодельным распределением его в пространстве.

3.2 Уравнения состояния

Уравнение состояния, соответствующее (\ref{DefTs}), можно представить в такой форме: $$\label{EqBIG}p = K_0 e^{s/c_v} \rho^{\gamma},~~K_0=Q_0 {\cal A} \mu_g^{-1}.\tag{3.5}$$ Для процессов (\ref{DefSt1}) это уравнение можно записать так: $$\label{EqBIG1} p = K_0 \sigma(t) {\cal S}(\xi,\zeta) \rho^{\gamma}.\tag{3.6}$$ Здесь $\sigma(t)=e^{s_0(t)/c_v}$ и ${\cal S}(\xi,\zeta) = e^{s_a(\xi,\zeta)/c_v}$. Соответствующее соотношение для температуры будет иметь такой вид: $$\label{EqT1} T = K_0 \sigma(t) {\cal S}(\xi,\zeta) \rho^{\gamma-1}=\Pi(t){\cal T}(\xi,\zeta),\tag{3.7}$$ где $$\Pi(t)=K_0\sigma(t)M_0^{\gamma-1}a^{-2(\gamma-1)}b^{-\gamma+1},$$ $$\label{DefcT} {\cal T}(\xi,\zeta)={\cal S}(\xi,\zeta){\cal R}^{\gamma-1}(\xi,\zeta).\tag{3.8}$$
     Квазиадиабатические процессы, соответствующие (\ref{DefSt1}), можно рассматривать и для анализа эволюции звездной структуры в автомодельном режиме [2,3]. В этом случае необходимо к уравнениям состояния добавлять уравнения, позволяющие описывать функцию ${\cal S}(\xi,\zeta)$ с помощью уравнений теплопередачи в звездах с учетом объемного энерговыделения в них. Однако эта задача, как уже отмечалось, требует отдельного анализа, выходящего за рамки данной работы. Далее будут рассмотрены модели с однородным (${\cal S}(\xi,\zeta)\equiv 1$) и с неоднородным политропным распределениями энтропии ${\cal S}(\xi,\zeta)\sim {\cal R}^\delta$, где $\delta$ - некоторая постоянная. В последнем случае, пользуясь автомодельностью распределения энтропии, можно полагать, что ${\cal S}(\xi,\zeta)$ может быть задана в начальный момент времени. Подобный подход используется в случае анализа моделей взрыва в звездах [2].

4. Уравнения для гидродинамического потока и разделение переменных

Сформулированные общие положения позволяют получить уравнения для всех автомодельных переменных среды, включая маркеры ${\cal E}_{j},~j=1,2$ и также коэффициенты плотности ${\cal R}$ и температуры ${\cal T}$. Используя (\ref{Defea}), (\ref{DefrhoR}), (\ref{EqArz}) и (\ref{Defv}),  уравнения (\ref{Equ1}) можно привести к следующему виду: $$\label{EquwE} a(\dot{H}+H^2)\xi  - \frac{V^2(\xi,\zeta)}{a^3\xi^3} = {\cal F}^1_A -\frac{2\pi G M_0}{a\xi}|J|K_1+\Phi_r,\tag{4.1}$$ $$b(\dot{F}+F^2)\zeta = {\cal F}^2_A  -\frac{2\pi G M_0}{a\xi}|J|K_2+\Phi_z.$$ Эти уравнения представляют собой уравнения для маркеров ${\cal E}^1(\xi,\zeta),~{\cal E}^2(\xi,\zeta)$. В них ${\cal F}^1_A,~{\cal F}_A^2$ - компоненты силы Архимеда по соответствующим осям координат: $$\label{EqFA1}{\cal F}^1_A=-\frac{\Pi(t)}{a{\cal R}}\frac{\partial}{\partial \xi}({\cal S}{\cal R}^{\gamma}),~~{\cal F}^2_A=-\frac{\Pi(t)}{b{\cal R}}\frac{\partial}{\partial \zeta}({\cal S}{\cal R}^{\gamma}).\tag{4.2}$$ Здесь предполагается выполнение уравнения состояния (\ref{EqBIG1}).
       Для полного описания распределения и эволюции всех составляющих динамики среды необходимо решать пару уравнений (\ref{EquwE}) относительно ${\cal E}^1(\xi,\zeta),~{\cal E}^2(\xi,\zeta)$. Поскольку эти уравнения записаны в автомодельных переменных с коэффициентами, зависящими от времени, для построения решений этих уравнений необходимо в каждом из них разделить переменную $t$ и пространственные переменные $\xi,~\zeta$. Чтобы проделать такую процедуру, перепишем уравнения (\ref{EquwE}), используя (\ref{DefKe}) в следующем виде: $$\label{EqSys0} a(\dot{H}+H^2)\xi  - \frac{V^2(\xi,\zeta)}{a^3\xi^3} = -\frac{\Pi(t)}{a}\frac{1}{{\cal R}}\frac{\partial}{\partial \xi}\Big({\cal S}{\cal R}^{\gamma}\Big) -\frac{2\pi G M_0}{a^2}{\cal K}_1+\frac{1}{a}\Phi_{\xi},\tag{4.3}$$ $$b(\dot{F}+F^2)\zeta = -\frac{\Pi(t)}{b}\frac{1}{{\cal R}}\frac{\partial}{\partial \zeta}\Big({\cal S}{\cal R}^{\gamma}\Big) -\frac{2\pi G M_0}{a^2}{\cal K}_2+\frac{1}{b}\Phi_{\zeta}.$$ Здесь введены обозначения: $$   {\cal K}_1 =\frac{a}{b}\frac{1}{\xi}\left(\frac{\partial {\cal E}^2}{\partial \zeta}{\cal E}^1-\frac{\partial {\cal E}^1}{\partial \zeta}{\cal E}^2\right),$$ $${\cal K}_2= \frac{1}{\xi}\left(\frac{\partial {\cal E}^1}{\partial \xi}{\cal E}^2-\frac{\partial {\cal E}^2}{\partial \xi}{\cal E}^1\right).$$ Заметим, что ${\cal K}_1$ и ${\cal K}_2$ удовлетворяют тождеству: $$\label{EuvK12} \frac{1}{\xi}\frac{\partial}{\partial\xi}\left(\xi{\cal K}_1\right)+ \frac{a}{b}\frac{\partial{\cal K}_2}{\partial\zeta}=2{\cal R}.\tag{4.4}$$ Поскольку ${\cal K}_1,~{\cal K}_2$ и ${\cal R}$ зависят только от $\xi$ и $\zeta$, из последнего соотношения следует требование: $b=\beta a(t)$. Параметр $\beta$ можно назвать параметром анизотропии эволюции газодинамической структуры.
     Необходимым условием разделения переменных является требование выполнения соотношения: $$\label{DefV2} V^2 = \mu \xi^4 + h(\xi),\tag{4.5}$$ где $\mu>0$ - постоянная, а $h(\xi)$ - вспомогательная функция, требующая уточнения. Физический смысл $\mu$ и $h$ устанавливается после подстановки (\ref{DefV2}) в (\ref{Defv}). В результате находим, что слагаемое с коэффициентом $\mu$ связано с вращением системы как твердого тела, а слагаемое с $h$ описывает дифференциальное вращение.
     Представим произвольную пока функцию $\Phi$ в следующем виде: $$\label{DefPhi} \Phi = \frac{2\pi G M_0}{a}\Phi_0(\xi,\zeta) + \frac{n(\xi)}{a^2} + \frac{b^2 \mu}{2a^4}\zeta^2,\tag{4.6}$$ где $\Phi_0(\xi,\zeta)$ и $n(\xi)$ - некоторые вспомогательные функции, требующие уточнения их смысла. Подставляя теперь (\ref{DefPhi}) и (\ref{DefV2}) в уравнения системы (\ref{EqSys0}), получаем: $$\label{EqSys1} \Big[a(\dot{H}+H^2)-\frac{f}{a^3}\Big]\xi - \frac{h(\xi)}{a^3\xi^3} = -\frac{{\cal P}(t)}{a}\frac{1}{{\cal R}}\frac{\partial}{\partial \xi}\Big({\cal S}{\cal R}^{\gamma}\Big) -\frac{2\pi G M_0}{a^2}\Big({\cal K}_1+\Phi_{0,\xi}\Big)+ \frac{n'(\xi)}{a^3},\tag{4.7}$$ $$ b\Big[(\dot{F}+F^2)-\frac{f}{a^4}\Big]\zeta = -\frac{{\cal P}(t)}{b}\frac{1}{{\cal R}}\frac{\partial}{\partial \zeta}\Big({\cal S}{\cal R}^{\gamma}\Big)  -\frac{2\pi G M_0}{a^2}\Big({\cal K}_2+\frac{a}{b}\Phi_{0,\zeta}\Big).$$
    Условиями разделения переменных в этих уравнениях теперь являются следующие соотношения: $$\label{VarPG1}\frac{a\Pi(t)}{2\pi G M_0}=\frac{K_0M_0^{\gamma-2}\beta^{1-\gamma}}{4\pi G }\sigma(t)a^{4-3\gamma} = Q_1={\rm const};\tag{4.8}$$ $$  a^3\Big(\dot{H}+H^2\Big)-\frac{\mu}{a}=2\pi G M_0\Lambda,$$ $$  h = -\xi^3 n'(\xi).$$ Кроме этого, необходимо, чтобы разделение переменных было выполнено в уравнении для функции $\Phi$ с учетом соотношения (\ref{EqPhi}). В результате соответствующих вычислений, приходим к (\ref{Defh}) и (\ref{Defn}) для $h$ и $n$ (см. Приложение).
     Результатом процедуры разделения переменных являются уравнения (\ref{EqSys1}): $$\label{EqSys2}\Lambda\xi+\frac{Q_1}{{\cal R}}\frac{\partial}{\partial \xi}\Big({\cal S}{\cal R}^{\gamma}\Big) +{\cal K}_1+\Phi_{0,\xi}=0,$$ $$ \beta\Lambda\zeta +\frac{Q_1}{\beta{\cal R}}\frac{\partial}{\partial \zeta}\Big({\cal S}{\cal R}^{\gamma}\Big) + {\cal K}_2+\frac{1}{\beta}\Phi_{0,\zeta}=0.$$
     Основной задачей данной работы является получение и анализ решений относительно распределения плотности среды и эволюции масштабных факторов. Для решения этой задачи вместо построения решений системы уравнений (\ref{EqSys2}) относительно ${\cal E}^1$ и ${\cal E}^2$ достаточно решать уравнение динамического равновесия. Вычисляя дивергенцию этих двух уравнений в переменных $\xi$ и $\zeta$ и учитывая то, что функция $\Phi_0$ удовлетворяет уравнению (\ref{EqPhi0}) (см. Приложение), приходим к модифицированному уравнению Лейна-Эмдена для функции ${\cal R}$: $$\label{EqGLER}\lambda + {\cal R}+\frac{Q_1}{2}\left[\frac{1}{\xi}\frac{\partial}{\partial \xi}\left(\frac{\xi}{{\cal R}}\frac{\partial}{\partial \xi}\Big({\cal S}{\cal R}^{\gamma}\Big)\right)+\frac{1}{\beta^2}\frac{\partial}{\partial \zeta}\left(\frac{1}{{\cal R}}\frac{\partial}{\partial \zeta}\Big({\cal S}{\cal R}^{\gamma}\Big)\right)\right]=0.\tag{4.9}$$  Параметр $\lambda=3\Lambda/2$ будем далее называть параметром динамического равновесия. Знак и величина этого параметра определяют характер и величину отклонения системы от точного баланса сил Архимеда и тяготения.
    В соответствии с (\ref{VarPG1}) физический смысл параметра $\nu$ и, соответственно, параметра $\lambda$, состоит в том, что они определяют локальную силу реакции среды на ускоренное ее расширение или сжатие, вызванную нарушением баланса сил тяготения и Архимеда. Обычно строение звезд рассматривается в предположении их статического равновесия, когда в каждой точке среды сила тяготения в точности уравновешивается силой Архимеда. Такому равновесию соответствует значение $\lambda=0$. В реальности, если слои звезды смещаются в радиальном направлении и имеется зональный поток, то баланс силы тяготения и Архимеда нарушается. При этом в системе возникают потоки радиального и зонального перемещения точек среды, приводящие к автомодельной  эволюции. В статическом случае $a(t)\equiv {\rm const}$ выполняется условие баланса сил  и уравнения модели формально переходят в уравнения статической теории строения звезд [1,3] с $\lambda=0$. Как будет ясно из дальнейшего, дополнительная сила реакции среды, связанная с $\lambda$, играет важную роль в структуре звезд и космологических потоков газа, находящихся не в статическом, а динамическом равновесии.

5. Эволюция структуры со временем

Автомодельная эволюция газодинамической структуры описывается третьим уравнением  системы (\ref{VarPG1}), в соответствии с которым происходит растяжение или сжатие структуры в зависимости от изменений со временем масштабного фактора $a(t)$.  Это уравнение перепишем в следующем виде: $$\label{Eqa} \ddot{a} = \mu a^{-3} + \nu a^{-2}.\tag{5.1}$$ Здесь введено обозначение: $$\label{Defmn} \nu = \frac{4\pi G M_0}{3\beta} \lambda.\tag{5.2}$$
     Для удобства дальнейшего качественного анализа решений уравнения (\ref{Eqa}),  представим его в форме динамической системы: $$\label{EqDynSys} \dot{c} = \frac{\mu}{a^3}+\frac{\nu}{a^2},~~\dot{a} = c.\tag{5.3}$$ Эту систему удобно привести к безразмерному виду, вводя новые переменные: $$ x = a/a_0,~~y = t_0 c/a_0,~~\tau = t/t_0,$$ где $$\label{Defa0t0} a_0 = \mu/|\nu|,~~t_0 = \frac{\mu^{3/2}}{|\nu|^2}.\tag{5.4}$$ В этом случае система (\ref{EqDynSys}) приобретает вид: $$\label{Eqxy}\frac{dy}{d\tau} = x^{-3}+{\rm sign}(\nu) x^{-2},~~\frac{dx}{d\tau} = y,\tag{5.5}$$ в котором отсутствуют свободные параметры, кроме знака величины $\nu$.
     Динамическая система (\ref{Eqxy}) имеет в случае $\nu >0$ одну особую точку, а в случае $\nu<0$ - две. Общей для обоих знаков $\nu$  особой точкой является точка $(x_{\infty}=\infty,~~c_{\infty}=0)$. В случае $\nu <0$ дополнительной особой точкой является точка: $x_0=1,~y_0=0$, что соответствует $a_0=\mu/|\nu|$. Именно эта точка представляет особый интерес с точки зрения существования автомодельных осцилляций структуры при сохранении их динамического равновесия. Полагая вблизи этой точки $x = 1 + \eta(t),~~y=\delta$, где $\eta$ и $\delta$ - бесконечно малые величины первого порядка малости, приходим к линеаризованной системе: $$\label{LinDynSys}\dot{\eta} = \delta,~~\dot{\delta} = - \eta.\tag{5.6}$$ Отсюда следует, что особая точка $x_0=1,~y_0=0$ является центром, а размерная угловая частота $\Omega_0$ бесконечно малых колебаний вблизи этого центра равна: $$\label{DefgO} \Omega_0 =\frac{1}{t_0} = \frac{|\nu|^2}{\mu^{3/2}}.\tag{5.7}$$ Таким образом, при $\nu < 0$ для начальных условий вблизи особой точки с $a_0=\mu/|\nu|$ эволюция газодинамической структуры представляет собой колебания с частотой близкой к $\Omega_0$.
     Динамическая система (\ref{Eqxy}) имеет интеграл движения: $$\label{DefE} \frac{y^2}{2}+{\rm sign}(\nu)\frac{1}{x}+\frac{1}{2x^2}=E,\tag{5.8}$$ который аналогичен интегралу энергии частицы, совершающей одномерное движение в потенциальном поле сил.

5.1. Фазовые портреты при $\nu<0$

Фазовые траектории динамической системы (\ref{Eqxy}), соответствующие (\ref{DefE}) для различных значений $E$  при $\nu < 0$, приведены на диаграмме рис. 5.1. Особая точка системы обозначена на диаграмме рис. 5.1 под номером 0. Жирной линией под номером 4 обозначена фазовая траектория, соответствующая значению $E=0$. Все траектории для $-0.5< E <0$ являются замкнутыми, а траектории c $E>0$ асимптотически стремятся к точкам $(x=\infty,~y=\pm\sqrt{2E})$ при $t\to\pm\infty$. Из (\ref{DefE}) следует, что фазовые траектории для $-0.5< E <0$  пересекают ось абсцисс при значениях безразмерной координаты, равной:
$$\label{Defxpm} x_{\pm} = \frac{1}{1\pm\sqrt{2E+1}}.\tag{5.9}$$ Точка $x_{+}$ соответствует максимальному сжатию структуры, а точка $x_{-}$ - максимальному расширению. Размах колебаний $\Delta_E=|x_{-}-x_{+}|$ в случае осцилляций определяется следующим образом:
$$\label{DefhE} \Delta_E = |x_{-}-x_{+}| = \frac{\sqrt{1-2|E|}}{|E|}.\tag{5.10}$$ Для $E=0$ $x_{-}=\infty$, а при $E>0$ эта точка лежит в отрицательной области значений $x_{-}<0$, но траектории в полуплоскости $x<0$ не имеют физического смысла.
     Период колебаний $P_{E}$ газодинамического объекта, соответствующий определенному значению параметра $E$, вычисляется в соответствии со следующей формулой: $$\label{EqTE}P_{E} = 2\int\limits_{x_{+}}^{x_{-}}\frac{xdx}{\sqrt{2Ex^2+2x-1}}=\frac{\pi\sqrt{2}}{2|E|^{3/2}}.\tag{5.11}$$ Как следует из этого соотношения при $E\to 0 $ период колебаний стремится к бесконечности.
     Таким образом, в случае $\nu < 0$ и $-0.5<E<0$ газодинамическая система представляет собой осциллирующую астрофизическую структуру сжимающуюся и расширяющуюся со временем с периодом, который определяется параметром $\Omega_0$. В дальнейшем свяжем данные структуры со звездами, совершающими осцилляции. Основной причиной возникновения осцилляций является периодическая перекачка энергии от кинетической энергии радиального сжатия или расширения к энергии зонального потока и потенциальной энергии силы тяготения при неизменном балансе сил тяготения, Архимеда и реакции среды.  Когда звезда автомодельно расширяется с увеличением масштабного фактора $a$, кинетическая энергия среды, запасаемая в радиальном потоке, убывает, а разность потенциальной энергия среды в поле тяготения и энергии зонального потока увеличивается. На обратном ходе цикла колебаний кинетическая энергия зонального потока увеличивается, а разность потенциальной энергии и энергии зонального потока уменьшается. При $\mu=0$, т.е. при отсутствии зонального потока, колебательный режим невозможен, поскольку сам знак потенциальной энергии не меняется в процессе эволюции. Такая ситуация соответствует чисто радиальной модели, описанной в [12].  Такой тип осцилляций не требует наличия в звезде слоя переионизации газа, который необходим для механизма осцилляций, предложенного Жевакиным С.А. [32,33,34] для цефеид. Следовательно, механизм осцилляций, соответствующий предлагаемой модели, возможен на любой стадии эволюции звезд, но может иметь различные варианты параметров осцилляций.

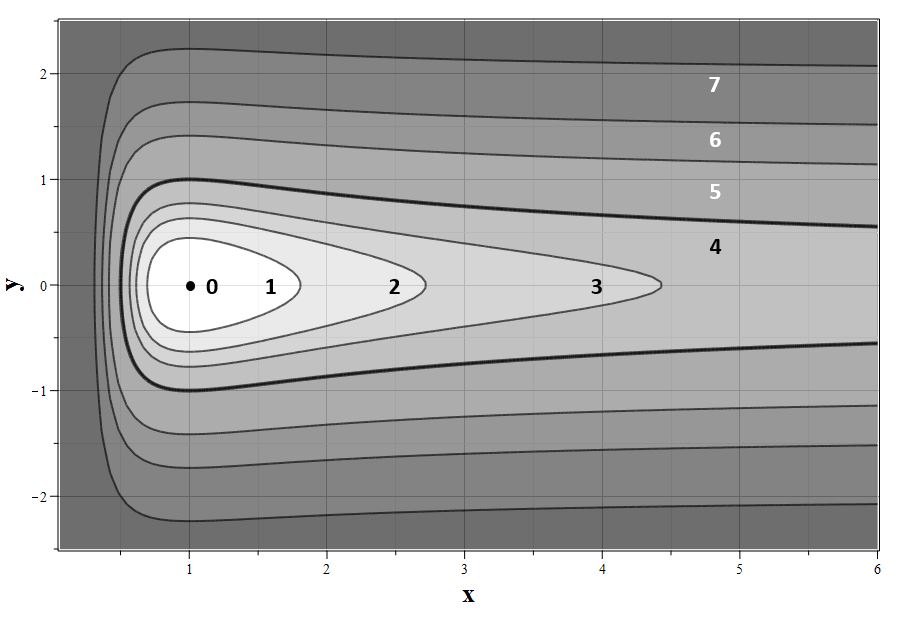Рис. 5.1. Фазовый портрет (\ref{Eqxy}) для $\nu<0$: $E=-0.5\, (0)$, $E=-0.4\, (1)$,  $E=-0.3\, (2)$, $E=-0.2\, (3)$, $E=0.0\, (4)$, $E=0.5\, (5)$, $E=1.0\, (6)$, $E=2.0\, (7)$

5.2. Фазовые портреты при $\nu>0$

Фазовые траектории динамической системы (\ref{Eqxy}) для $\nu>0$ приведены на диаграмме рис. 5.2. Допустимыми значениями параметра $E$ для данных траекторий являются значения $E >0$. Траектории на диаграмме рис. 5.2 пересекают ось абсцисс в точках: $$x_E = \frac{1}{-1+\sqrt{2E+1}}.$$ Эта точка соответствует максимальному возможному сжатию структуры и достигается только, если в начальный момент времени $y(0)<0$. Исходя из соотношения (\ref{DefE}) находим, что при $\tau\to \infty$ скорость расширения автомодельной структуры стремится к постоянному значению $y_{\infty}$, которое определяется величиной энергетического параметра $E$: $$\label{Defyinf} y_{\infty} = \sqrt{2E}.\tag{5.12}$$ Соответствующее значение $E$ определяет и асимптотическую скорость сжатия при $t\to -\infty$, равное $y_{-\infty}=-\sqrt{2E}$.
 

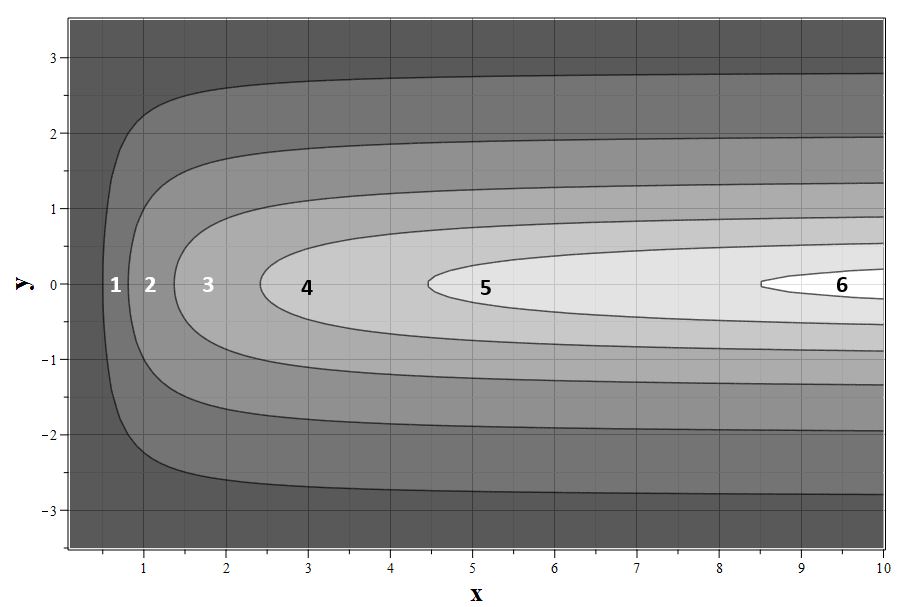Рис. 5.2. Фазовый портрет (\ref{Eqxy}) для $\nu>0$: $E=0.125\, (1)$, $E=0.25\, (2)$, $E=0.5\, (3)$, $E=1.0\, (4)$, $E=2.0\, (5)$, $E=4.0\, (6)$

6. Пространственное распределение газа в автомодельных переменных

Рассмотрим теперь пространственную структуру распределения плотности, температуры и других параметров среды, которые соответствуют рассмотренной автомодельной эволюции звезд.  Эти распределения описываются уравнением (\ref{EqGLER}). Приведем это уравнение к следующему виду: $$\label{EqREL} \frac{1}{\xi}\frac{\partial}{\partial\xi}\left(\xi\Big(\frac{\gamma-1}{\gamma}{\cal S}_{\xi}{\cal T}+S{\cal T}_{\xi}\Big)\right)+ \frac{\partial}{\partial\eta}\Big(\frac{\gamma-1}{\gamma}{\cal S}_{\eta}{\cal T}+S{\cal T}_{\eta}\Big)+{\cal T}^{n}+\lambda=0.\tag{6.1}$$ Здесь введены обозначения $\eta = \beta\zeta = z/a(t)$ и $n=(\gamma-1)^{-1}$ - показатель политропы. При выводе этого уравнения, учитывая произвол в выборе параметра $K_0$, параметр $Q_1$ в (\ref{EqGLER}) был выбран в соответствии с соотношением: $$\frac{\gamma}{2(\gamma-1)} Q_1 =1.$$ Заметим, что в случае сферической симметрии распределения плотности в газодинамической структуре при условиях: ${\cal S}(\xi,\eta)=S_0={\rm const}$ и $\lambda=0$, уравнение (\ref{EqREL}) превращается в классическое уравнение звездных политроп Лейна-Эмдена (LEm) [18,19,1,3]. Уравнение Lem при $a(t)=a_0={\rm const}$ описывает статическое распределение плотности и температуры в нормальных звездах с политропным уравнением состоянием газа (плазмы). В рамках же расширенной теории, когда $\lambda\not = 0$ и $a=a(t)$, это уравнение описывает нестатические астрофизические (и космологические) объекты c автомодельной структурой. Модели же с функцией ${\cal S}(\xi,\eta)$, отличной от постоянной, позволяют учитывать теплопередачу в газе. Поэтому уравнение (\ref{EqREL}) можно рассматривать как двумерное обобщение уравнения Лейна-Эмдена.
     Существенным отличием рассматриваемой в данной работе модели от модели Лейна-Эмдена является отсутствие полной сферической симметрии в распределении плотности и других параметров среды. Это отличие является принципиальным, но может быть малым. Полная сферическая симметрия означает, что все параметры среды, включая маркеры $e^1,e^2$, зависят только от сферической координаты $\chi=\sqrt{\xi^2+\eta^2}$. Однако в этом случае имеем: $$|{\cal J}| = \frac{\partial {\cal E}^1}{\partial \xi} \frac{\partial {\cal E}^2}{\partial \zeta}-\frac{\partial {\cal E}^1}{\partial \zeta} \frac{\partial {\cal E}^2}{\partial \xi} =\left(\frac{\partial {\cal E}^1}{\partial \chi} \frac{\partial {\cal E}^2}{\partial \chi}-\frac{\partial {\cal E}^1}{\partial \chi} \frac{\partial {\cal E}^2}{\partial \chi}\right)\frac{\xi\zeta}{\chi^2}=0.$$ Отсюда следует, что и $\rho = a^{-3}\beta^{-1}M_0|{\cal J}|/\xi=0$, т.е. плотность среды в таком представлении оказывается нулевой. Поэтому маркеры должны обязательно зависеть от двух координатных переменных. Вместе с этим реальные астрофизические структуры очень часто обладают пространственными симметриями. К таким объектам относятся звезды и спиральные галактики. Звезды в большинстве своем обладают почти точной сферической симметрией, отклонения от которой в случае одиночных звезд обусловлены их вращением. Для Солнца эффект нарушения сферической симметрии мало заметен. Тем не менее, наличие дифференциального вращения Солнца указывает на отклонения от его сферической симметрии, что проявляется и в распределении магнитного поля по его поверхности. В отличие от звезд спиральные галактики и другие аналогичные структуры представляют собой почти плоские тонкие диски. В таких структурах скорость изменения плотности вдоль оси вращения существенно больше, чем вдоль радиальной координаты в плоскости диска.  Эллиптические галактики и быстро вращающиеся звезды занимают промежуточное положение между одиночными звездами и спиральными галактиками. В качестве основной цели исследований в данной работе будут рассмотрены звезды с относительно медленным вращением. Галактики и другие типы объектов следует рассматривать в отдельной работе.
     Для описания почти сферических звезд перейдем в уравнении (\ref{EqREL}) от цилиндрических координат к сферическим. Соответственно уравнение (\ref{EqREL}) примет следующий вид: $$\label{EqRELr} \frac{1}{\chi^2}\frac{\partial}{\partial\chi}\left(\chi^2\Big(\frac{\gamma-1}{\gamma}{\cal {\cal S}}_{\chi}{\cal T}+{\cal S}{\cal T}_{\chi}\Big)\right)+ \frac{1}{\chi^2\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta\Big(\frac{\gamma-1}{\gamma}{\cal {\cal S}}_{\theta}{\cal T}+{\cal S}{\cal T}_{\theta}\Big)\right)+{\cal T}^{n}+\lambda=0.\tag{6.2}$$ Здесь $\chi=\sqrt{\xi^2+\eta^2}$ и $\theta = \arctan(\xi/\eta)$ - радиальная координата и полярный угол соответственно. По аналогии с моделями Лейна-Эмдена в качестве граничных условий для безразмерной функции ${\cal R}(\chi,\theta)$, записанной в сферических координатах, будем рассматривать два условия: $$\label{DefBR}{\cal R}(0,\theta)=1,~~\left.\frac{\partial}{\partial \chi}{\cal R}(\chi,\theta)\right|_{\chi=0}=0.\tag{6.3}$$   Первое из этих условий фактически связывает масштаб плотности газа в исследуемых объектах, например, неопределенный пока параметр $M_0$, с его плотностью  в центре поля. Второе условие необходимо для того, чтобы исключить сингулярные в центре поля решения. Отсюда также следует граничное условие для ${\cal S}(\chi,\theta)$: $$\label{DefBS}\left.\frac{\partial}{\partial \chi}{\cal S}(\chi,\theta)\right|_{\chi=0}=0,\tag{6.4}$$ которое также необходимо для исключения сингулярных в точке $\chi=0$ решений в случае неоднородного распределения энтропии. Граничным условием по угловой координате, как обычно, следует считать условие периодичности.
     Предположим, что функция ${\cal S}(\chi,\theta)$ может быть представлена в виде ряда:   $$\label{DSefSRow} {\cal S} = {\cal S}_0(\chi) + \sum\limits_{k=1}^{\infty}\varsigma^k {\cal S}_k(\chi,\theta).\tag{6.5}$$ тогда решение уравнения (\ref{EqRELr}) можно искать в виде аналогичного ряда: $$\label{DefSolT} {\cal T} = {\cal T}_0(\chi) + \sum\limits_{k=1}^{\infty}\varsigma^k {\cal T}_k(\chi,\theta),\tag{6.6}$$ где $\varsigma$ - малый параметр, характеризующий отклонение автомодельного распределения плотности и температуры от сферически симметричной формы. Подставляя (\ref{DefSolT}) в уравнение (\ref{EqRELr}), можно получить уравнения для всех функций ${\cal T}_{k}$ .  В нулевом порядке уравнение выглядит следующим образом:   $$\label{EqT0} \frac{1}{\chi^2}\frac{\partial}{\partial\chi}\left(\chi^2\Big(\frac{\gamma-1}{\gamma}{\cal S}_{0,\chi}{\cal T}_0+S_0{\cal T}_{0,\chi}\Big)\right)+{\cal T}_0^{n}+\lambda=0.\tag{6.7}$$ Граничные условия для ${\cal T}_0$ будут иметь такой вид: $$\label{DefBCT0}{\cal T}_0(0)=1,~~{\cal T}'_0(0) =0.\tag{6.8}$$  Уравнение этого типа при ${\cal S}_0=1$ рассматривалось в [12] для анализа автомодельной эволюции центрально симметричных астрофизических структур.
    В первом порядке теории возмущений имеем следующее линейное уравнение для функции ${\cal T}_1$: $$\frac{1}{\chi^2}\frac{\partial}{\partial\chi}\left(\chi^2\Big(\frac{\gamma-1}{\gamma}{\cal S}_{0,\chi}{\cal T}_1+S_0{\cal T}_{1,\chi}\Big)\right)+n{\cal T}_0^{n-1}(\chi){\cal T}_1+$$ $$\label{EqTp1}+\frac{1}{\chi^2\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta\Big(\frac{\gamma-1}{\gamma}{\cal S}_{0,\theta}{\cal T}_1+S_0{\cal T}_{1,\theta}\Big)\right)=F_1(\chi,\theta),\tag{6.9}$$ с однородными граничными условиями: $$ {\cal T}_1(0,\theta)=0,~~{\cal T}'_1(0,\theta) =0.$$ Функция $F_1(\chi,\theta)$ имеет при этом такой вид: $$F_1=-\frac{1}{\chi^2}\frac{\partial}{\partial\chi}\left(\chi^2\Big(\frac{\gamma-1}{\gamma}{\cal S}_{1,\chi}{\cal T}_0+S_1{\cal T}_{0,\chi}\Big)\right)-\frac{1}{\chi^2\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta\Big(\frac{\gamma-1}{\gamma}{\cal S}_{1,\theta}{\cal T}_0\Big)\right).$$ Уравнение (\ref{EqTp1}) для однородной части решения допускает разделение переменных, поэтому $${\cal T}_1 = \sum\limits_{l=0}^{\infty}R_{l}(\chi){\cal P}_{l}(\cos\theta).  $$ Здесь ${\cal P}_{l}(\cos(\theta))$ - функции, удовлетворяющие уравнениям: $$ \frac{1}{\chi^2\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta\Big(\frac{\gamma-1}{\gamma}{\cal S}_{0,\theta}{\cal P}_{l}+S_0{\cal P}_{l,\theta}\Big)\right)+\Lambda(l){\cal P}_l=0.$$ Это уравнение в случае ${\cal S}=1$ переходит в классическое уравнение Лежандра для одноименных полиномов $P_{l}(\cos\theta),~~l=0,\dots,\infty$ с собственным числом $\Lambda=l(l+1)$. Функции $R_l(\chi)$ являются  собственными функциями радиального уравнения: $$\label{EqRl}\frac{1}{\chi^2}\frac{\partial}{\partial\chi}\left(\chi^2\Big(\frac{\gamma-1}{\gamma}{\cal S}_{0,\chi}R_l+S_0 R_{l,\chi}\Big)\right)+n{\cal T}_0^{n-1}(\chi)R_l=\Lambda(l) R_l;\tag{6.10}$$ с граничными условиями: $R_l(0)=0,~~R'_{l}(0)=0$.
     Несмотря на всю важность анализа возмущений, в данной работе этот анализ проводится не будет. Такие вычисления удобно представлять в отдельной работе. Поэтому далее основное внимание будет уделено анализу уравнения (\ref{EqT0}), которое можно назвать модифицированным уравнением Лейна\,--\,Эмдена (mLEm), от которого это уравнение отличается лишь наличием аддитивной постоянной $\lambda\not=0$.
     Кроме этого, следует отметить, что в теории строения звезд используют граничные условия для температуры и давления на поверхности звезды, где ${\cal R}(\chi,\theta)$ обращается по определению в ноль [1,3]. При этом могут возникать определенные проблемы, связанные с тем, что плотность и температура могут обращаться в ноль не при одном и том же значении $r$.  Как будет ясно из дальнейшего, условие обращения в ноль плотности на поверхности звезды, которое на самом деле является приближенным, в наиболее интересном классе моделей c $\lambda<0$ не выполняется. В таких моделях для определения радиуса звезды следует использовать положение первого минимума плотности или температуры. Такое определение более точно отражает суть физических процессов, формирующих звезды и другие астрофизические структуры.
 
6. Модели с однородным распределением энтропии. Точные решения для $n=1$

Начнем анализ моделей пространственной структуры с наиболее простых моделей, имеющих однородное распределение энтропии, полагая ${\cal S}_0(\chi)=1$. Целью дальнейшего анализа является получение общей информации о распределении плотности в сферическом приближении для случая $\lambda\not=0$. Это означает, что далее будут исследоваться свойства функций ${\cal R}$ и ${\cal T}$ в нулевом приближении. В силу этого для упрощения записи индекс $0$ у функций ${\cal S}_0(\chi),~{\cal R}_0(\chi)$ и ${\cal T}_0(\chi)$ будет опускаться.
     Как хорошо известно [1,3], уравнения LEm имеют несколько точных решений. Одно из них соответствует показателю политропы $n=1$, что эквивалентно $\gamma=2$. Для этого случая уравнение (\ref{EqT0}) принимает следующий вид: $$\frac{d^2}{d\chi^2}{\cal Z}+ {\cal Z}+\chi \lambda=0.$$ Здесь введено обозначение ${\cal Z}=\chi {\cal T}$. Это линейное уравнение имеет решение: $$ {\cal Z} = C_1 \sin( \chi)+C_2\cos( \chi) - \chi \lambda.$$   Удовлетворяя граничным условиям, находим: $C_2=0,~~C_1-\lambda=1.$ В результате решение для ${\cal T}$  примет такой вид: $$\label{SolQn1}{\cal T}(\chi)= (1+ \lambda)\frac{1}{\chi}\sin(\chi) - \lambda.\tag{6.1}$$ Отсюда видно, что при $\chi\to\infty$ ${\cal T}(\chi)\to - \lambda$. В случае $\lambda > 0$, предельное значение плотности оказывается отрицательным, что означает, что коэффициент температуры ${\cal T}(\chi)$ и ${\cal R}(\chi)$  обращаются в некоторой точке в ноль. Обращение плотности в ноль при некотором значении $\chi_0$ трактуется в теории LEm как существование его конечного радиуса $r_{0}$, который в данной теории будет зависеть от времени: $r_0 =a(t)\chi_0$.
     В случае $\lambda < 0$ предельное значение плотности на бесконечности оказывается положительным и почти постоянным, т.е. при удалении от центра системы ${\cal T}$ (${\cal R}$) осциллирует, но приближается к постоянной величине ${\cal T}_{\infty}$. Анализируя (\ref{SolQn1}), устанавливаем, что существует такой диапазон отрицательных значений $\lambda$: $\lambda_{cr} \ge \lambda < 0$, в котором ${\cal T}(\chi)$ принимает отрицательные значения, хотя при $\chi\to\infty$ ${\cal T}(\chi)$ cтремится к положительному значению. Это аналогично моделям с положительными $\lambda$ в классической модели LEm. В отличие от этого при $\lambda < \lambda_{cr}$ коэффициент температуры ${\cal T}(\chi)$ оказывается всюду положительной величиной.  Для модели c $n=1$ величину $\lambda_{cr}$ можно найти из соотношения $\lambda_{cr}=\sin(z_0)/(z_0-\sin(z_0))$, где $z_0$ - минимальное положительное решение уравнения: $z=\tan(z)$, которое эквивалентно уравнениям на экстремумы функции ${\cal T}(z)$ (\ref{SolQn1}). Численно наxодим $\lambda_{cr}\simeq -0.1784650236$.
      Еще одной особенностью решения (\ref{SolQn1})  является то, что при $\lambda=-1$ функция ${\cal T}(\chi)$ всюду оказывается равной $1$. Такое решение соответствует однородному пространственному распределению температуры, плотности и давления в газе, что  характерно  для космологических моделей.
    На рис. 3 представлены кривые коэффициента температуры ${\cal T}(\chi)$ для положительных значений $\lambda$ и $n=1$. Точками показана кривая, соответствующая классической теории Лейна-Эмдена c $\lambda=0$.  Из графиков видно, что с увеличением $\lambda$ радиус сферы, на которой температура, плотность и давление обращаются в ноль (т.е., по определению, радиус звезды), уменьшается.

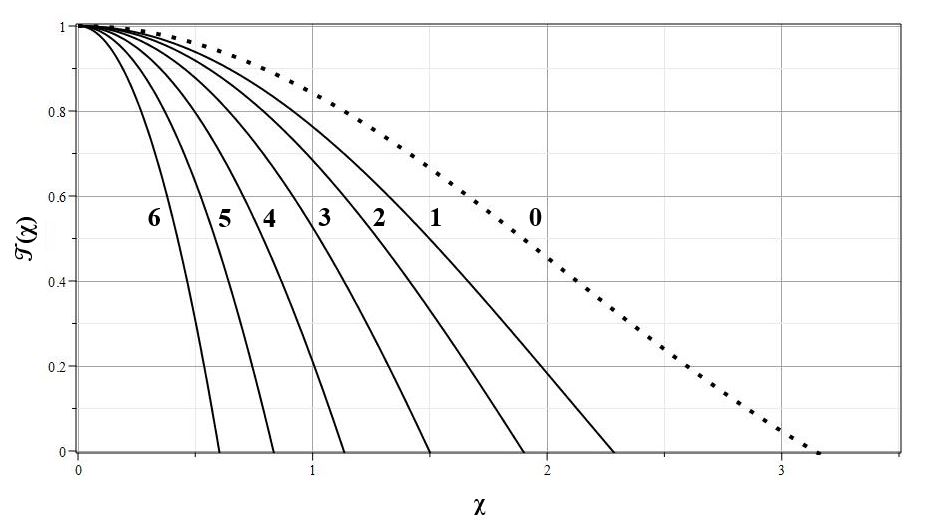Рис. 3. Коэффициент температуры ${\cal T}(\chi)$ для $n=1$ и $\lambda>0$: $\lambda=0  (0)$ $\lambda=0.5  (1)$,  $\lambda=1.0  (2)$,   $\lambda=2.0 (3)$,  $\lambda=4.0  (4)$,  $\lambda=8.0  (5)$,  $\lambda=16.0  (6)$

    На рис. 4 изображены кривые ${\cal T}(\chi)$ для $\lambda<0$. Как и на рис. 3 точками обозначена кривая, соответствующая $\lambda=0$. Пунктиром - кривая, соответствующая значению $\lambda=-0.1784650236$, при котором кривая в одной точке касается оси абсцисс.
 

Рис. 4. Коэффициент температуры ${\cal T}(\chi)$ для $\lambda<0$: $\lambda=0 (0)$,  $\lambda=-0.1784650236 (1)$, $\lambda=-0.25 (2)$, $\lambda=-0.5 (3)$,  $\lambda=-0.75  (4)$,\ $\lambda=-1.0 (5)$, $\lambda=-1.25  (6)$,  $\lambda=-1.5  (7)$, $\lambda=-1.75  (8)$, $\lambda=-2.0 (9)$

    Заметим, что точные решения для модели LEm, как и для mLEm можно также найти при $\gamma=\infty$ ($n=0$) (несжимаемая жидкость) и $\gamma=6/5$ ($n=5$) [3].

7. Модели c $n\not=1$

7.1. Модели с $\lambda > 0$

Рассмотрим теперь характерные особенности моделей c $n\not=1$ для случая положительных значений параметра динамического равновесия: $\lambda>0$. В качестве примера рассмотрим модель одноатомного газа с $\gamma=5/3$ и $n=3/2$. Как и в случае точного решения, рассмотренного выше, при $\lambda>0$ поведение параметров среды подобно поведению этих параметров в соответствующих моделях LEm с $\lambda=0$.
     Для того, чтобы показать это, представим уравнение (\ref{EqT0}) в таком виде: $$\label{EqT0S1}\frac{d^2}{d\chi^2} {\cal T} +\frac{2}{\chi}\frac{d}{d\chi}{\cal T} + {\cal T}^{n}+\lambda=0,\tag{7.1}$$ Отсюда видно, что при стремлении производных ${\cal T}''(\chi)$ и ${\cal T}'(\chi)$ на бесконечности к нулю, имеем: ${\cal T}^{n}\to -\lambda <0$. Однако последнее для вещественных решений невозможно, если $\lambda>0$ и показатель политропы $n=(\gamma-1)^{-1}$ отличается от нечетного целого числа. Это означает, что для граничного условия ${\cal T}(0)=1$ вещественное решение в случае  $\lambda>0$ может существовать на некотором отрезке вблизи нуля и обращается в ноль в некоторой точке $\chi_0$: ${\cal T}(\chi_0)=0$. Для случая нечетных $n$ будут существовать решения и на некоторых других интервалах $\chi$, как это имеет место для $n=1~(\gamma=2)$.
     Для иллюстрации такого поведения на рис. 5 приведены графики ${\cal T}(\chi)$ для нескольких значений $n$ при $\lambda=0.25$.

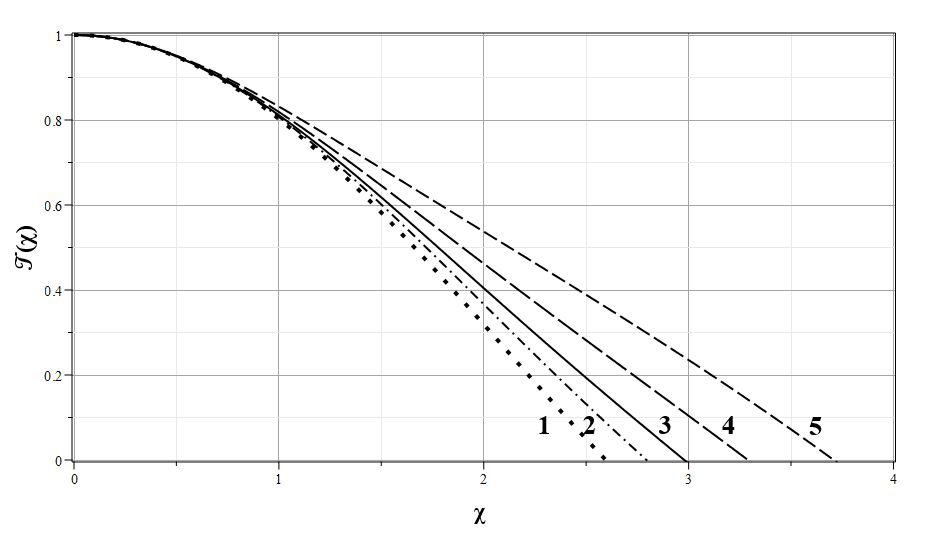Рис. 5. Коэффициент температуры ${\cal T}(\chi)$ для $\lambda=0.25$: $n=1 (1)$, $n=1.5 (2)$, $n=2.0 (3)$, $n=3.0 (4)$, $n=5.0 (5)$

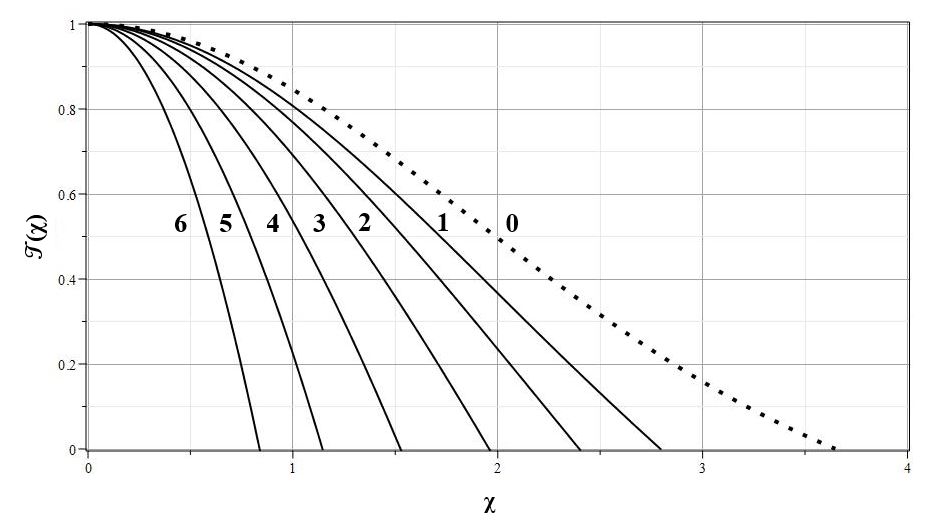Рис. 6. Коэффициент температуры ${\cal T}(\chi)$ для одноатомного газа с $n=3/2 (\gamma=5/3)$ и $\lambda>0$: $\lambda=0 (0)$, $\lambda=0.5  (1)$, $\lambda=1.0  (2)$, $\lambda=1.5  (3)$, $\lambda=2.0  (4)$, $\lambda=4.0  (5)$, $\lambda=8.0  (6)$

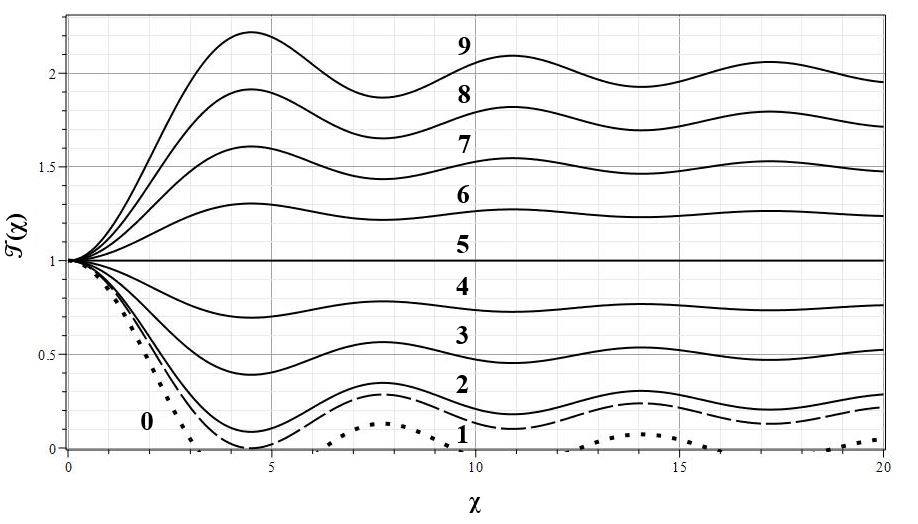
На рис. 6 приведены графики ${\cal T}(\chi)$ для набора положительных значений параметра $\lambda\ge 0$ для показателя адиабаты одноатомного газа с $\gamma=5/3$ и $n=3/2$. Значение $\lambda=0$ соответствует стандартной модели LEm. Таким образом, модели с $\lambda>0$ в целом похожи на модели LEm, но при одном и том же $n$ имеют меньший автомодельный радиус звезды.
     Сопоставляя приведенный анализ с анализом эволюции масштабного фактора, находим, что модели с $\lambda >0$ не могут описывать какие-либо статические структуры. При $t\to\infty$ в соответствии с (\ref{Defyinf}) эволюция обязательно переходит в режим расширения с постоянной скоростью $u_{\infty}=\lim\limits_{t\to\infty}\dot{a}=a_0y_{\infty}/t_0$. При достаточно малых значениях параметра энергии $E$ эта асимптотическая скорость может быть достаточно маленькой, чтобы имелась возможность сопоставить ее реальному автомодельному расширению звезд. Однако наличие отрицательных значений плотности и температуры при значениях $\chi >\chi_0$ делает эти модели менее пригодными для сопоставления с реальными данными, чем модели с $\lambda<0$.

7.2. Модели с $\lambda <0$

В отличие от моделей c $\lambda>0$ модели с отрицательными значениями этого параметра, как и в случае точного решения c $n=1$, демонстрируют иное асимптотическое поведение ${\cal T}(\chi)$ при $\chi\to\infty$. Важным является то, что при $\chi\to\infty$ величина ${\cal T}(\chi)$ стремится к постоянному значению, которое определяется формулой: $$\label{Defqinf}      \lim\limits_{\chi\to \infty}{\cal T}(\chi)={\cal T}_{\infty}= |\lambda|^{1/n}.\tag{7.2}$$ Это можно доказать, рассматривая приближенное асимптотическое решение уравнения (\ref{EqT0S1})  вида: $${\cal T}(\chi) = {\cal T}_{\infty} +  q(\chi),$$ где $|q(\chi)|<< 1$. В результате уравнение для $q(\chi)$ линеаризуется. Если ввести вместо $q(\chi)$ функцию $w=\chi q(\chi)$, то для $w(\chi)$ уравнение приводится к следующему виду: $$w''+ n {\cal T}_{\infty}^{n-1} w=0.$$ Отсюда находим, что решение для $w(\chi)$ будет иметь такой вид: $$w = W_0 \sin(K \chi),$$ и, соответственно, для $q(\chi)$ - следующий: $$\label{Solq} q = W_0 \frac{1}{\chi}\sin(K \chi).\tag{7.3}$$ Здесь $K= \sqrt{n {\cal T}_{\infty}^{n-1}}=\sqrt{n} |\lambda|^{(n-1)/(2n)}$. Параметр $K$ определяет длину осцилляций плотности при $\chi\to\infty$. Значение $W_0$ находится из граничного условия ${\cal T}(0)=1$: $$W_0 =\frac{1-{\cal T}_{\infty}}{K}=\frac{1-|\lambda|^{1/n}}{K}.$$ Окончательно находим: $$\label{SolQLn} {\cal T}\simeq q{\cal T}_{\infty} +   (1-{\cal T}_{\infty}) \frac{1}{K\chi}\sin(K \chi).\tag{7.4}$$ В частности,  для всех $n>1$ при $\lambda=1$  находим: $W_0=0$, что эквивалентно отсутствию пространственных осцилляций. Этот факт подтверждают и численные расчеты, приведенные ниже. Полезно отметить для более точного понимания физического смысла параметра $\lambda$, что согласно (\ref{Defqinf}), величина $|\lambda|$ совпадает со значением коэффициента плотности среды на бесконечности: ${\cal R}_{\infty}=\lim_{\xi\to\infty}{\cal R}(\xi)$.
     По аналогии с точным решением при $n=1$ можно приближенно рассчитать значение $\lambda_{cr}(n)$, при котором кривая ${\cal T}(\chi)$ касается единственный раз оси абсцисс. Условием этого является обращение ${\cal T}(\chi)$ из (\ref{SolQLn}) в ноль и обращение в ноль производной ${\cal T}'(\chi)$ в этой же точке. Эти два условия имеют вид: $${\cal T}(\chi_0)={\cal T}_{\infty} +   (1-{\cal T}_{\infty}) \frac{\sin(K \chi_0)}{K \chi_0}=0,$$ $${\cal T}'(\chi_0)= \frac{W_0\cos(K\chi_0)}{K \chi_0^2}\Big(K \chi_0 - \tan(K\chi_0)\Big)=0.$$ Второе уравнение этой системы: $$\tan(K\chi_0)=K\chi_0$$ решается независимо. Минимальный положительный корень этого уравнения равен: $$K\chi_0 \simeq 4.493409458.$$
     Из первого уравнения находим:    $${\cal T}_{\infty}= |\lambda|^{1/n} = -\frac{{\cal T}_0}{1-{\cal T}_0}\simeq 0.1784650236.$$ Отсюда: $$\lambda_{cr}(n)\simeq -{\cal T}_{\infty}^n.$$ В частности, для $n=3/2$ ($\gamma=5/3$): $$\lambda_{cr}(3/2) \simeq -0.07539276488.$$ Более точное значение, полученное численным подбором решения, дает оценку $\lambda_{cr}(3/2) \simeq -0.085$. Аналогично, для $n=3$ ($\gamma=4/3$) имеем оценку по приближенному решению: $\lambda_{cr}(3)=-0.005684069$, а согласно численному решению: $\lambda_{cr}(3) =-0.0065$.
     На рис. 7 и 8 представлены графики изменения ${\cal T}(\chi)$ для различных значений $\lambda$ для одноатомного газа с $\gamma=5/3$ и ультрарелятивистского электронного газа с $\gamma=4/3$. Кривые на этих графиках демонстрируют все основные особенности пространственного распределения температуры, рассмотренные выше. В частности, при $\lambda=1$ в пространственном распределении ${\cal T}(\chi)$ отсутствуют осцилляции.

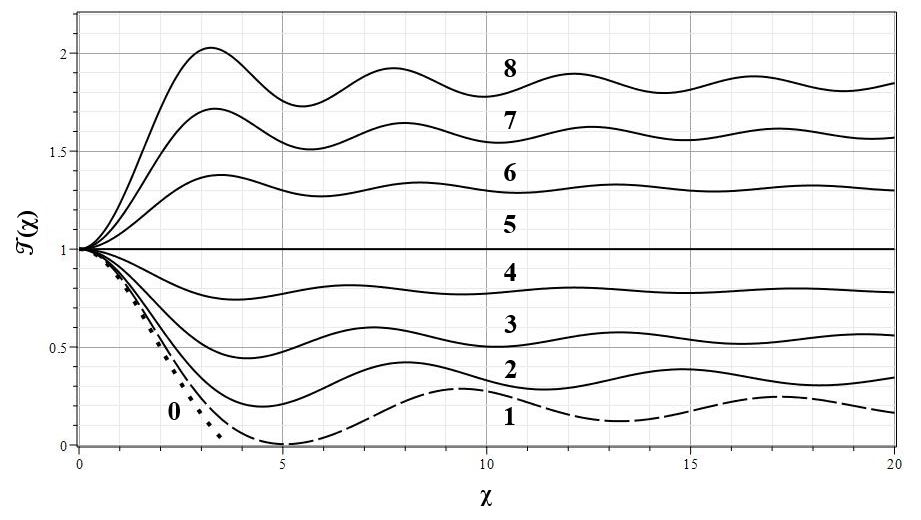Рис. 7. Коэффициент температуры ${\cal T}(\chi)$ для одноатомного газа с $n=3/2(\gamma=5/3)$ и $\lambda>0$: $\lambda=0  (0)$,$\lambda=-0.085  (1)$, $\lambda=-0.2  (2)$, $\lambda=-0.4  (3)$, $\lambda=-0.7  (4)$, $\lambda=-1.0  (5)$, $\lambda=-1.5  (6)$, $\lambda=-2.0  (7)$, $\lambda=-2.5  (8)$

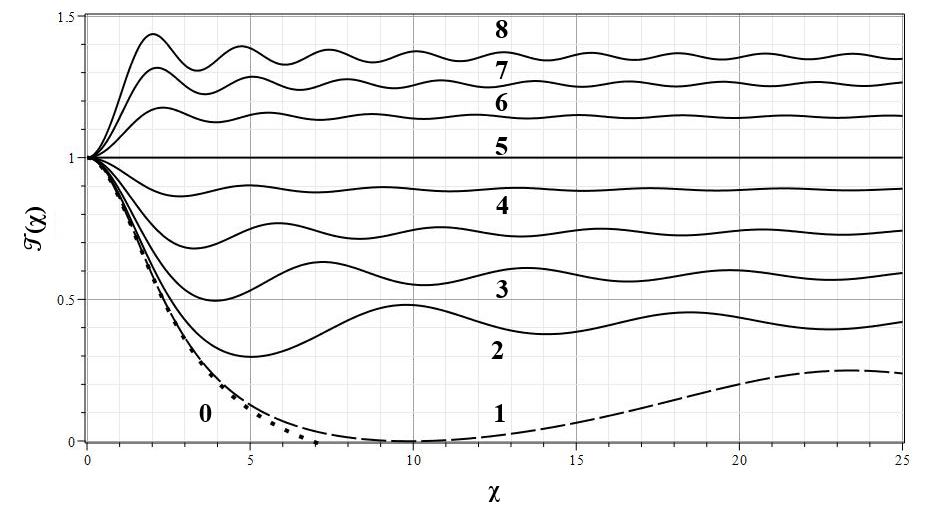Рис. 8. Коэффициент температуры ${\cal T}(\chi)$ для ультрарелятивистского электронного газа с $n=3~(\gamma=4/3)$ и $\lambda>0$: $\lambda=0  (0)$, $\lambda=-0.0065  (1)$,  $\lambda=-0.2  (2)$,  $\lambda=-0.4  (3)$,  $\lambda=-0.7  (4)$,  $\lambda=-1.0  (5)$,  $\lambda=-1.5  (6)$,  $\lambda=-2.0  (7)$,  $\lambda=-2.5  (8)$

Как показывает анализ точного решения для $n=1$, так и численного для $n>1$, весь диапазон отрицательных значений параметра динамического равновесия $\lambda$ можно разделить на три интервала, в которых поведение коэффициентов плотности, температуры и давления существенно отличаются. Первый интервал $[\lambda_{cr}(n),0]$ отличается тем, что в этом диапазоне значений $\lambda$ коэффициент температуры ${\cal T}$ конечное число раз обращается в ноль, что аналогично поведению температуры для классических моделей LEm с $\lambda=0$. Как и в классических моделях LEm участки с положительной плотностью перемежаются с участками, где вещественного решения не существует. Однако в отличие от моделей LEm в пределе при $\chi\to\infty$ значение коэффициента температуры стремится к положительному значению $q_{\infty}$.
     Второй открытый интервал $(-1,\lambda_{cr}(n))$ характеризуется тем, что температура нигде не обращается в ноль и, совершая осцилляции с волновым числом $K(n,\lambda)$, стремится к $q_{\infty}$. Для этого интервала важным является то, что колебания температуры нигде не превышают значения $1$. В этом отношении модели из этого диапазона значений $\lambda$ подобны классическим моделям LEm. Поскольку для этих моделей положительные решения для плотности и температуры существуют всюду, то такую модель можно рассматривать как модель политропной звезды с пространственными осцилляциями температуры и плотности, затухающими вдали от звезды.
     Третий интервал $(-\infty,-1)$ соответствует моделям с почти однородным при $\lambda<-1$ и однородным при $\lambda=-1$ пространственным распределением плотности и температуры. Такие модели можно использовать для описания космологического расширения в классическом приближении. Пространственные осцилляции ${\cal T}$, соответствующие (\ref{SolQLn}), можно при этом сопоставить известным реально наблюдаемым пространственным космологическим осцилляциям температуры [29]. Такие осцилляции обнаруживают в форме акустического пика в спектре флуктуаций температуры.
     Важной особенностью построенных решений, которая воспроизводится во всех моделях с $\lambda <0$, является поведение коэффициентов температуры и плотности при $\chi\to \infty$. Из соотношения (\ref{Defqinf} следует, что величина ${\cal R}_{\infty}=|\lambda|$ определяет плотность газа $\rho_{\infty}=M_0a^{-2}b^{-1}{\cal R}_{\infty}=M_0a^{-2}b^{-1}|\lambda|$ на бесконечности. Это означает, что модели mLEm, основанные на уравнении (\ref{EqRELr}), как и модели LEm с $\lambda=0$, адекватно описывают распределение плотности лишь на ограниченном расстоянии от центра звезды. В моделях LEm ограничиваются расстояниями, на которых плотность остается вещественной и не отрицательной. В рассматриваемых в данной работе моделях mLEm с $\lambda<0$ также приходится ограничиваться конечными расстояниями от центра звезды. Если считать, что звезда является единственным объектом в пространстве, то на больших расстояниях от нее плотность должна убывать достаточно быстро так, чтобы общая масса газа была бы конечной величиной. В реальности звезды находятся в некотором окружении. Поэтому плотность среды на большом удалении от звезд не стремится к нулю. Формально это означает, что на определенном расстоянии от звезды должна возникать ударная волна, соответствующая переходному процессу от плотности газа, связанного со звездой, к плотности межзвездной среды. Как хорошо известно, такие волны наблюдаются в реальности. При этом следует подчеркнуть, что при сферически симметричном распределении плотности, поле тяготения, порождаемое газом вне некоторой сферы, окружающей звезду, не оказывает влияния на процессы внутри этой сферы. Поэтому формальное ограничение модели конечными расстояниями не меняет физической сути построений для рассматриваемых моделей.

8. Модели динамического равновесия осциллирующих звезд

Собирая полученную информацию о свойствах рассмотренных моделей, можно предположить, что наиболее адекватными по отношению к реальному строению звезд и их эволюции являются модели с $\lambda$ в диапазоне значений $(-1,\lambda_{cr})$. Действительно, поскольку для моделей из этого диапазона $\lambda$ плотность и температура газа всюду положительны, то модель может, хотя бы на качественном уровне, быть сопоставлена реальным данным без потери физического смысла на всех расстояниях от условной поверхности звезды.  В классических моделях LEm всегда существуют области пространства, в которых отсутствуют вещественные положительные решения для температуры и плотности.
    Если отложить пока вопрос о теплопередаче в исследуемой структуре, то более точный отбор моделей по величине $\lambda$ может осуществляться с помощью двух основных параметров пространственной структуры. Первый параметр - это значение температуры газа в первом минимуме с автомодельной координатой $\chi_0$, отсчитывая от $\chi=0$ (см. рис. 9), который в структуре нормальных звезд можно отождествить с условным радиусом звезды, т.е. с минимумом температуры в  фотосфере. Второй - это значение ${\cal T}$ в первом после минимума в точке $\chi_0$ максимуме температуры.
      Важность этих параметров состоит в том, что их можно просто соотнести с известными данными о строении Солнца, исходя из стандартной его модели.
 

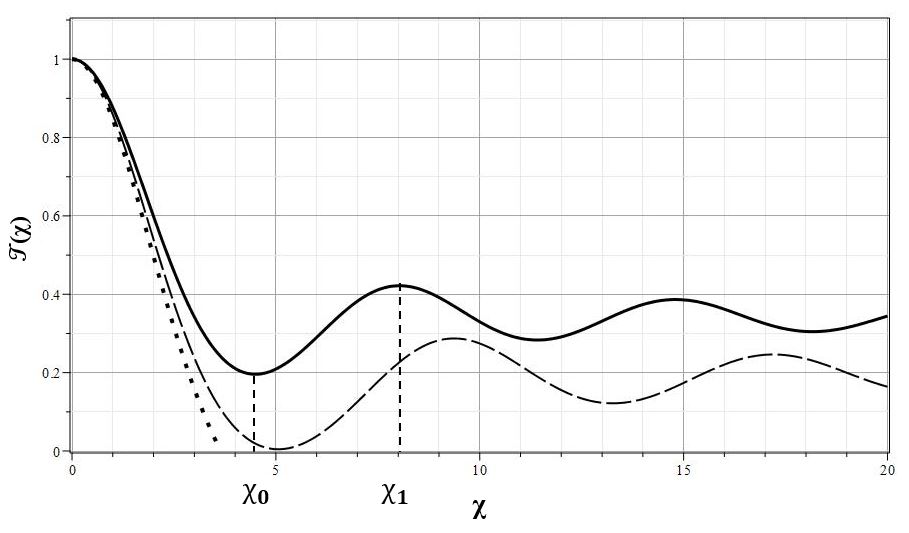Рис. 9. Коэффициент температуры ${\cal T}(\chi)$ для одноатомного газа с $n=3/2~(\gamma=5/3)$: $\lambda=0$ - точки, $\lambda=\lambda_{cr}=-0.0851$ - пунктир, $\lambda=-0.2<\lambda_{cr}$ - сплошная линия, $\chi_0$ - первый минимум, $\chi_1$ - первый максимум

На рис. 9 представлены кривые коэффициента температуры ${\cal T}(\chi)$, соответствующие нулевому значению $\lambda=0$ (точки) и $\lambda\simeq \lambda_{cr}$ (сплошная кривая) для одноатомного газа $n=3/2$.  Для этой кривой указаны положения первого минимума $\chi_0$ и первого максимума $\chi_1$ коэффициента температуры. Как отмечалось  выше, первый минимум температуры может быть сопоставлен минимуму в фотосфере звезды. Для Солнца оценка равновесной температуры в центре соответствует примерно $15\cdot 10^{6} K$, а минимальная температура в фотосфере - $4800 K$ [8,30]. Таким образом, минимум температуры примерно в $3000$ раз меньше температуры в центре Солнца. Отсюда следует, что реальное значение параметра $\lambda$ для Солнца и, по всей видимости, для звезд других типов, должно быть близко к критическому значению $\lambda_{cr}$. Для одноатомного газа в модели с постоянной энтропией $\lambda_{cr}\simeq -0.085$.
    Это значение автоматически определяет температуру  газа вдали от звезды: ${\cal T}_{\infty}\simeq =0.1934$ (штрих-пунктирная прямая). Если принимать, что в центре звезды температура $15\cdot 10^{6} K$, то температура вдали от звезды будет примерно $T_{\infty}\simeq 15\cdot 10^{6}{\cal T}_{\infty} \simeq 3\cdot 10^{6}$. Очевидно, что это завышенная оценка связана с тем, что при ее получении не учитывалась теплопередача в газе, потеря тепла за счет излучения и, возможно, влияние магнитного поля.
      Вторым важным элементом автомодельной структуры является немонотонный характер изменения температуры и плотности с расстоянием от центра поля. Наличие первого максимума $\chi_1$ можно отождествить с наблюдаемым реально максимумом температуры в короне Солнца [30,8]. Если отождествить положение первого минимума температуры с радиусом звезды, то следующий максимум находится на расстоянии чуть меньше радиуса звезды от ее поверхности. Величина ${\cal T}_{max}={\cal T}(\chi_1)$ в максимуме $\chi_1$ для кривой с критическим значением $\lambda$ равна ${\cal T}_{max} = \simeq 0.3$.
    Соответственно для Солнца находим: $T_{max} = 15\cdot 10^{6}{\cal T}_{max} \simeq 5\cdot 10^{6}$. Это тоже завышенная оценка, что также по всей видимости, связано с неучтенной теплопередачей. Вместе с тем можно констатировать, что данная модель дает качественное объяснение росту температуры в короне Солнца.
    Осциллирующий характер пространственного распределения температуры и плотности в данной модели связан с динамическиим влиянием ускоренного течения газа вне звезды. В сочетании с тем, что при таких значениях $\lambda<0$ и $E<0$ в (\ref{DefE}) структура переходит в режим осцилляций во времени, рассмотренные модели представляются наиболее адекватными для сопоставления реальной структуре Солнца. Некоторые недостатки модели можно устранить с помощью учета теплопередачи в среде.

9. Радиальные осцилляции звезд

9.1. Параметры звездных осцилляций

Для более детального понимания свойств рассматриваемой модели рассмотрим особенности эволюции структуры звезд с $\lambda < \lambda_{cr}$ в режиме осцилляций. Для того, чтобы связать параметры модели с реальными данными о звездах, в том числе, данными о Солнце, будем следовать следующим достаточно очевидным предположениям. Во-первых, положение первого минимума $\chi_0$ в распределении температуры, как уже отмечалось, будем интерпретировать как автомодельный радиус звезды. Поэтому  $\chi_0=R_*/a_*$, где $R_*$ - текущий радиус звезды, определяемый по минимуму температуры в фотосфере. Отсюда текущее значение масштабного фактора можно оценить следующим образом $a_*=R_*/\chi_0$. Во-вторых, исходя из соотношения для плотности (\ref{DefrhoR}), можно оценить масштаб массы $M_0$, зная плотность вещества звезды в ее центре. Из граничного условия в центре звезды ${\cal R}(0)=1$ следует: $$\label{DefM0} M_0 = a_*^3\beta\rho(0).\tag{9.1}$$ В результате имеем $$\label{DefnuM0} \nu = \frac{4\pi G M_0}{3\beta} |\lambda_{*}| = \frac{4\pi G }{3} a_*^3|\lambda_{*}|\rho(0).\tag{9.2}$$ Здесь $\lambda_*$ - значение параметра динамического равновесия, соответствующего текущему состоянию звезды.
      Рассмотрим звезды типа Солнца, осцилляции которых невелики, так что можно считать, что текущий масштабный фактор $a_*$ мало отличается от масштабного фактора, соответствующего особой точке фазовой диаграммы (рис. 1), т.е. $a_*=a_0$, где $a_0=\mu/|\nu|$. Из последнего соотношения можем вычислить параметр $\mu$: $$\label{Eqmua}\mu=a_*|\nu|.\tag{9.3}$$ Эти соотношения позволяют вычислить значение периода осцилляций вблизи особой точки. В соответствии с (\ref{Defmn}) находим:$$\label{DefT0}P_0 = 2\pi \frac{\mu^{3/2}}{|\nu|^{3/2}}=\sqrt{\frac{3\pi\beta}{|\lambda_*|\rho(0)G}}.\tag{9.4}$$ Эта формула показывает, что частота осцилляций звезды зависит от плотности в центре звезды $\rho(0)$, от значения параметра динамического равновесия $|\lambda_*|$  и от значения параметра анизотропии $\beta$, который для звезд с относительно малой скоростью вращения можно полагать равным 1: $\beta\simeq 1$. Формулу (\ref{DefT0}) можно сравнить с классической формулой периода пульсаций цефеид [9], которая имеет следующий вид: $$\label{EqP} P_{c} = \frac{1}{\sqrt{G\overline{\rho}}},\tag{9.5}$$ где $\overline{\rho}$ - средняя плотность вещества звезды. Сравнивая (\ref{DefT0}) с (\ref{EqP}) находим, что эти формулы совпадают, если выполнено равенство: $$\label{DefArho} \overline{\rho} = \frac{1}{3\pi\beta}|\lambda_*|\rho(0).\tag{9.6}$$   Фактическое совпадение соотношения (\ref{DefT0}) с (\ref{EqP}) при учете (\ref{DefArho}) означает, что полученные соотношения теории динамического равновесия почти сферических звезд могут служить нелинейной моделью теории звездных пульсаций, в том числе, цефеид.  С этой точки зрения (\ref{DefArho}) можно рассматривать как огрубленную интерпретацию частоты пульсаций с точки зрения линейной теории.

9.2. Диаграмма период-светимость
 
Наиболее важной практической целью теории звездных пульсаций является вывод диаграммы период-светимость, который играет важнейшую роль в использовании цефеид в качестве маркеров астрономических расстояний.
     Светимость $L$ по определению может быть вычислена как полный поток энергии излучения с поверхности звезды. Дифференциальный поток излучения вычисляется с помощью закона Стефана-Больцмана по формуле: $$F = \sigma_0 T^4(R_*)=\sigma_0 \Pi^4(t) {\cal T}^{4}(\chi_0).    $$ Здесь $\sigma_0$ - постоянная Стефана-Больцмана. Соответственно, светимость может вычислена с помощью соотношения: $$L = 4\pi \sigma_0 \Pi^4(t){\cal T}^4(\chi0) R^2_*=4\pi \sigma_0 \Pi^4(t)a^2(t){\cal T}^4(\chi0) \chi^2_0.$$ Согласно (\ref{VarPG1}) имеем: $$\Pi = 2\pi G M_0 Q_1 a^{-1}(t).$$ Учитывая (\ref{DefcT}) находим: $$\label{DefL} L = x^{-2}(t) {\cal L}_0,\tag{9.7}$$ где $$\label{DefL0} {\cal L}_0 = 4\pi \sigma_0 \left(\frac{4\pi G M_0 (\gamma-1)}{\gamma}\right)^4 a_{0}^{-2} {\cal T}^4(\chi0).$$
      Для построения диаграммы период-светимость воспользуемся соотношением (\ref{DefL}), записанным для максимального $x_{-}(E)$ и минимального $x_{+}(E)$ автомодельных радиусов звезд. В результате с учетом (\ref{Defxpm}) имеем: $$L_{max} = {\cal L}_0 \Big(1+\sqrt{1-2|E|}\Big)^{2},$$ $$L_{min} = {\cal L}_0 \Big(1-\sqrt{1-2|E|}\Big)^{2}.$$ Исключая из этих соотношений $E$ с помощью выражения (\ref{EqTE}), получаем формулы, которые по сути и являются диаграммами период-светимость: $$\label{DefIP} \frac{L_{max}}{{\cal L}_0}  = \left(1+\sqrt{1-\left(\frac{P_E}{2\pi}\right)^{-2/3}}\right)^{2},\tag{9.8}$$ $$\frac{L_{min}}{{\cal L}_0}  = \left(1-\sqrt{1-\left(\frac{P_E}{2\pi}\right)^{-2/3}}\right)^{2}.$$ Эти соотношения универсальны и не зависят от типа звезды. Реальные диаграммы период-светимость будут зависеть от двух параметров ${\cal L}_0$ и $t_0 = \mu^{3/2}/|\nu|^2$. В данной работе не ставилась цель провести сравнение реальных диаграмм период-светимость с диаграммами, соответствующими (\ref{DefIP}). Эта задача требует привлечения большого набора данных по цефеидам. В данной работе приводятся лишь графики универсальных кривых, соответствующих (\ref{DefIP}), а также универсальных кривых $x(\tau)$ и $y(\tau)$, соответствующих модели (\ref{Eqxy}).
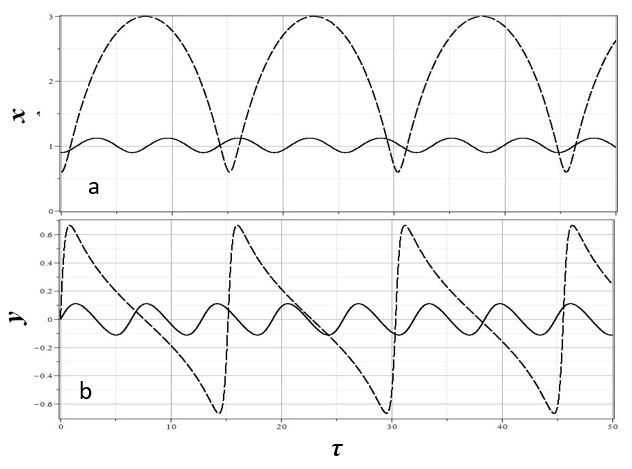
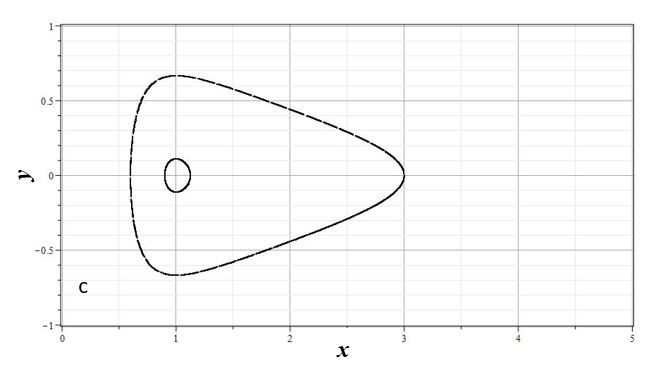
     Для наглядности характера осцилляций на рис. 10(a,b,c) представлены графики изменения безразмерного радиуса $x(\tau)$ (a) и безразмерной скорости $y(\tau)$ (b) изменения радиуса от безразмерного времени $\tau$ для $\lambda_*=-0.085$ и двух начальных  условий.
 

Рис. 10. Зависимость $x(\tau)$ (a) и $y(\tau)$ (b), а также фазовые траектории звезды (c) для $\lambda_*=-0.085$ c начальными условиями: 1 - $(y(0)=0,~x(0)=0.6)$ - пунктир, 2 - $(y(0)=0,~x(0)=0.9)$ - сплошная

Соответствующие кривые для относительных величин $L_{max}/{\cal L}_0$ и $L_{min}/{\cal L}_0$ представлены на рис. 11.  Верхний график (a) соответствует светимости звезд в максимуме, а (b) - в минимуме в зависимости от периода осцилляций звезд с одними и теми же параметрами, но для различных значений энергетического параметра $E$.
 

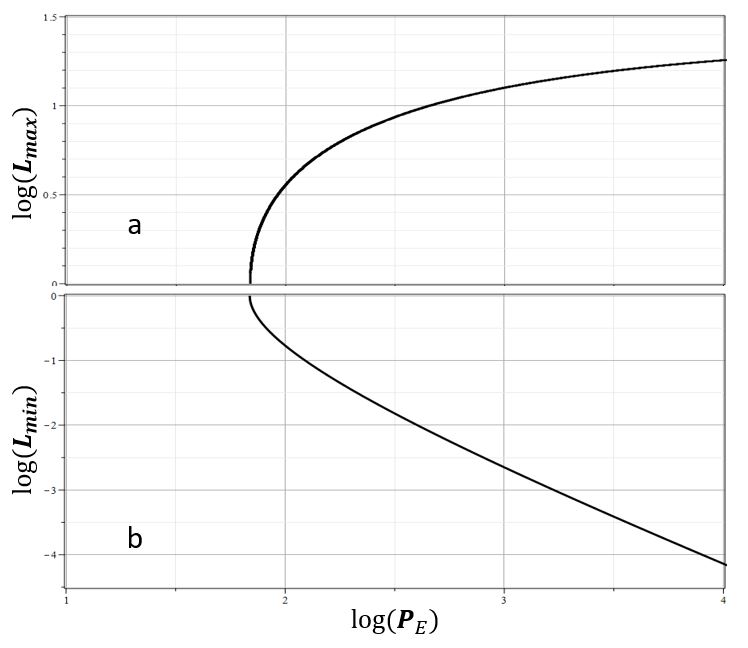Рис. 11. Диаграмма период-светимость соответствующая (\ref{DefIP})

Следует отметить, что полученное соотношение период-светимость (\ref{DefIP}) выражено в безразмерной форме. Поэтому его трудно сопоставлять с реальными эмпирическими диаграммами, полученными на основе реальных данных [9,11]. Тем не менее, общий вид диаграммы (\ref{DefIP}) в сравнении с реальными диаграммами указывает на их сходство. Это позволяет надеяться на возможность использования модели (\ref{Eqxy}) для описания звездных осцилляций цефеид.

10. Модели с неоднородным распределением энтропии

 Рассмотренные модели с $\lambda\in (-1,\lambda_{cr})$, как это следует из предыдущего анализа, дают картину эволюции звезд,  которая на качественном уровне может быть сопоставлена реальным астрофизическим данным. Вместе с тем, при попытках сопоставить числовые оценки c параметрами Солнца возникают определенные проблемы, хотя качественно выводы, основанные на представленной модели дают объяснение некоторым известным фактам, например, росту температуры в короне Солнца. Проводя оценку параметров модели с $\gamma=5/3$ ($n=3/2$) и однородным распределением энтропии с наблюдаемыми параметрами Солнца, можно убедиться, что они существенно отличаются друг от друга, либо в отношении строения, либо в отношении эволюции Солнца. Как показывает анализ, основной проблемой при сопоставлении с реальными данными является величина критического значения $\lambda_*=-0.085$ параметра динамического равновесия. Эта величина оказывается по модулю слишком большой для того, чтобы параметры модели были сопоставимы параметрам строения и эволюции Солнца.     
 Естественным способом коррекции модели с целью получения более реалистичных значений параметров Солнца является включение в модель неоднородного распределения коэффициента энтропии ${\cal S}(\chi,\theta)$.
     В общем случае модели с неоднородным распределением энтропии следует исследовать с использованием уравнений переноса излучения в звездах и в межзвездной среде [3,2]. Можно показать, что при некоторых предположениях относительно коэффициента непрозрачности среды и коэффициента энерговыделения в среде уравнения теплопередачи можно привести к автомодельному виду. В этом случае одно из уравнений системы будет уравнение (\ref{EqREL}). Однако исследования такого рода удобнее проводить в отдельной работе. Тем не менее существует круг задач, в которых описание теплопередачи можно упростить и свести к задаче с некоторым заданным модельным распределением коэффициента энтропии ${\cal S}(\chi)$. Поскольку ${\cal S}(\chi)$ является функцией автомодельных переменных, то ее функциональный вид формально определяется распределением в начальный момент времени. В данной работе будет рассмотрена модельная функция ${\cal S}(\chi)$, зависящая от коэффициента плотности ${\cal R}(\chi)$ в соответствии с общим соотношением: $$\label{DefS} {\cal S}={\cal H}_0(\chi){\cal R}^{\delta}(\chi),\tag{10.1}$$  где ${\cal H}_0(\chi)>0$ - безразмерная функция радиальной координаты, необходимая для более точной коррекции потока тепла в звезде, а $\delta$ - некоторая безразмерная вещественные постоянная.
     Для первого этапа анализа, который реализуется далее, будем полагать  ${\cal H}_0={\rm const}$.  В этом случае величина ${\cal H}_0$ влияет лишь на масштаб радиальной координаты, поскольку может быть исключена из уравнения с помощью формальной замены: $\chi\to\chi'=\chi/\sqrt{{\cal H}_0}$. Это означает, что все вычисления можно проводить в предположении ${\cal H}_0=1$, а необходимые коррекции распределений в случае ${\cal H}_0\not=1$ можно сделать масштабированием радиальной координаты в полученном решении.
     Наиболее важным обстоятельством, связанным с соотношением (\ref{DefS}) при ${\cal H}_0={\rm const}$ является то, что эта формула фактически возвращает формулу для давления в среде к баротропному виду, но с новым эффективным показателем адиабаты $\sigma'=\sigma+\delta$. С точки зрения термодинамики это означает, что процесс автомодельной эволюции звезды, соответствующий (\ref{DefS}), является не адиабатическим, а политропным с показателем политропы: $$\label{Defm} m = \frac{n}{1 + n\delta}.\tag{10.2}$$ В случае адиабатической эволюции энтропия и количество тепла в слоях звезды не изменяются со временем. В случае же политропного режима энтропия среды изменяется и происходит перераспределение тепла, что и соответствует процессу теплопередачи. Этот процесс происходит так, что уравнение mLEm по форме не меняется, но меняется показатель политропы. В частности, это означает, что модифицированный показатель политропы в звездах типа Солнца может существенно отличаться от $n=3/2$. То же самое относится и к звездам других типов.
     Важность указанного вывода о политропном характере автомодельной эволюции, вытекающего из соотношения (\ref{DefS}), требует некоторых замечаний относительно применимости этого соотношения для описания реальных условий в звездах.  С формальной точки зрения в приближении радиального распределения параметров среды зависимость ${\cal S}(\chi)$ от $\chi$ почти всегда эквивалентна некоторой зависимости этой же функции от ${\cal R}(\chi)$. Конкретный же выбор зависимости  энтропии от плотности, соответствующий  (\ref{DefS}), может быть обоснован тем, что в теории строения и эволюции звезд [3,2] используются предположения о том, что энерговыделение в ядрах звезд, а также коэффициенты непрозрачности вещества являются степенными функциями температуры и плотности. С этой точки зрения соотношение (\ref{DefS}) выглядит достаточно адекватным.  Тем не менее, доказательство того, что модели, использующие (\ref{DefS}), соответствуют реальной структуре и эволюции звезд следует подтвердить сопоставлением расчетов в рамках рассматриваемых моделей с реальными данными. Для этого необходимо установить наиболее подходящую величину параметра $\delta$, параметров вращения $\mu$ и динамического равновесия $\lambda$, соответствующие тем или иным типам звезд. В данной работе такой анализ будет проведен в сопоставлении с данными о строении Солнца.
      Оптимальный выбор параметров модели для нормальных звезд типа Солнца c $\gamma=5/3,~n=3/2$ проводился перебором величин $\delta$ и $\lambda$ в диапазоне их значений, которые позволяли получить решения для распределений температуры и плотности, а также эволюционных траекторий звезды на фазовой диаграмме, которые наиболее точно согласовывались с реальными данными для Солнца. Из-за ограниченности объема статьи будут приведены результаты численных вычислений лишь для одного значения параметра $\delta$, который дает наиболее подходящие значения параметров модели Солнца в сопоставлении с реальными данными.
     Численный анализ проводился в c помощью средств Maple. Для численных расчетов использовалась процедура dsolve с применением подпрограммы dverk78. Для численного анализа автомодельного строения звезд уравнение (\ref{EqREL}) удобно переписать в следующем виде:   $$\label{EqST}\frac{d}{d\chi}{\cal F}+\frac{2}{\chi}{\cal F} + {\cal Q}^n+\lambda=0\tag{10.3}$$   где ${\cal Q} ={\cal R}^{\gamma-1}$ и ${\cal F}=S{\cal Q}'+S'{\cal Q}/(n+1)$. В этом случае коэффициент температуры ${\cal T}(\chi)$ будет вычисляться по формуле: ${\cal T} = {\cal S}(\chi){\cal Q}(\chi)$. Можно видеть, что в случае ${\cal S}(\chi)=1$ уравнение (\ref{EqST}) переходит в уравнения (\ref{EqT0S1}) модели mLEm, а ${\cal Q}(\chi)$ в ${\cal T}(\chi)$, при том же выборе параметров обезразмеривания переменных. Поскольку в уравнение (\ref{EqST}) входит функция ${\cal Q}(\chi)$, то соотношение (\ref{DefS}) удобно переписать в таком виде: $${\cal S}={\cal H}_0{\cal Q}^{k}(\chi),$$ где $k=n\delta$. В дальнейшем именно этот параметр будет использоваться для идентификации различных типов моделей. Следует отметить, что можно было бы решать уравнение (\ref{EqT0S1}). Как уже отмечалось, в случае ${\cal H}_0=1$ решения уравнений (\ref{EqST}) и (\ref{EqT0S1}) связаны некоторым масштабным преобразованием координат $\chi'=\chi/d$, где масштаб $d$ зависит от $n$, $\delta$. Чтобы не производить это дополнительное преобразование координат, численно решалось непосредственно уравнение (\ref{EqST}).
     В качестве примера на рис. 10 для иллюстрации результатов численных расчетов представлены распределения коэффициентов температуры для нескольких значений параметра $k$ при одном и том же значении параметра $\lambda=-0.0015$.

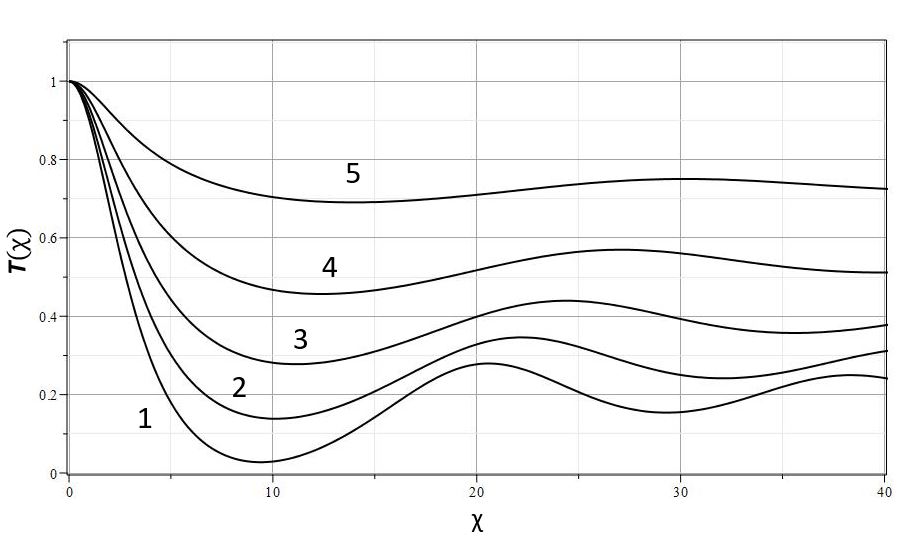Рис. 12. Коэффициент температуры ${\cal T}(\chi)$ для одноатомного газа с $n=3/2(\gamma=5/3)$ для $\lambda=-0.0015$: $k=-4/9  (1)$,  $k=-5/9  (2)$, $k=-6/9  (3)$,  $k=-7/9  (4)$, $k=-8/9  (5)$

11. Общая процедура оценивания параметров модели

Наиболее важными параметрами, которые полностью определяют пространственное автомодельное распределение плотности, температуры и энтропии, являются параметры $k$, $f$ ($\mu$)  и $\lambda$ ($\nu$). Параметр $f$ определяется скоростью зонального потока на экваторе звезды, но при его оценке имеется неопределенность, связанная с параметром $h_0$. Наличие не нулевого слагаемого с $h_0$ приводит к тому, что угловая скорость потока вблизи оси вращения стремится к бесконечности. Кроме этого, как следует из (\ref{DefPhi}), при $h_0\not=0$ связано с логарифмической особенностью в потенциале на оси вращения.  Это означает, что вблизи оси вращения модель должна быть уточнена в дальнейшем. Тем не менее, в дальнейшем именно выбор значения $h_0$ будет играть важную роль в подгонке модели под реальные данные.
      Выбор параметров $k$ и $\lambda$ также заранее не определен и может приводить к различным вариантам моделей звезды и ее эволюции. В частности, в зависимости от выбранных значений $k$ и $\lambda$ модель может соответствовать фазовой траектории звезды на диаграмме 1 с поступательным изменением ее радиуса в случае $E\ge 0$ или фазовой траектории в зоне осцилляций с $-0/5\le E <0$.
      Исходными данными, которые позволяют строить оценку параметров модели, соответствующей конкретной звезде, являются видимый радиус звезды, температура в фотосфере и  скорость зонального потока на экваторе. Для оценки параметра модели $M_0$ необходимо иметь оценку плотности массы в центре звезды. Вместе с тем оценка плотности в центре звезды сама зависит от типа модели. Тем не менее для простоты получения оценки в данной работе для Солнца будет использована классическая оценка $\rho(0)\simeq 150 [г/см^3]$, соответствующая стандартной модели Солнца. То же самое касается и температуры в центре Солнца $T_{\odot}\simeq 15\cdot 10^{6} K$ [8].
      Общая процедура построения модели конкретной звезды сводится к выбору определенных значений $k$ и $\lambda < \lambda_{cr}$ и вычислению соответствующей кривой распределения коэффициента температуры внутри звезды и за ее пределами. При заданном значении $k$ подбором $\lambda$ можно установить приближенно значение $\lambda_{cr}$, которое, как отмечалось ранее, соответствует условию касания кривых распределения ${\cal T}$ и ${\cal R}$ оси абсцисс. В точке касания плотность массы и температура для $\lambda=\lambda_{cr}$ обращаются в ноль. Далее, конкретные значения $\lambda_*$ должны выбираться в интервале $-1 <\lambda < \lambda_{cr}$. Выбор величины $\lambda_*$ может осуществляться уже из прямого сравнения результатов численного счета с реальными данными. Однако эту процедуру подбора $\lambda_*$ можно упростить, заменив ее процедурой подбора параметра $h_0$. Это можно сделать, исходя из предположения, что строится модель звезды, осцилляции которой происходят вблизи положения равновесия в особой точке с безразмерными координатами $x_*\simeq=1,~y_*\simeq 0$.
      Анализ полученных численным способом кривых распределения ${\cal T}$ сводится к вычислению положения первого минимума и следующего за ним максимума коэффициента температуры. Как уже отмечалось, первый минимум температуры и плотности по определению считается условной поверхностью звезды и связывается с минимумом температуры и плотности в ее фотосфере.  По форме кривой ${\cal T}={\cal T}(\chi)$ определяется положение первого минимума $\chi_0$ и текущего значения масштабного фактора $a_*=R_*/\chi_0$. Это позволяет оценить значение $M_0$ по формуле (\ref{DefM0}). В результате по формуле (\ref{DefnuM0}) для выбранного значения $\lambda_*$ можно оценить значение параметра $\nu$. Параметр $\mu$ должен вычисляться по формуле (\ref{Defmn}), исходя из значения параметра вращения $f$.
     Параметр вращения $f$ можно оценить по формуле (\ref{DefV2}), если известна скорость зонального потока $v_0$ на экваторе звезды. Формулу (\ref{DefV2}) c учетом (\ref{Defh}) полезно записать в таком виде: $$\label{Eqv}v = \frac{1}{a}\sqrt{f\xi^2+h_0}.\tag{11.1}$$ В эту формулу входит неопределенный параметр $h_0$, который описывает дифференциальное вращение звезды, но не влияет на другие оценки параметров звезды. Для того, чтобы скорость зонального потока $v(\xi,\zeta,t)$ принимала всюду только вещественные значения, достаточно, чтобы $h_0 \ge 0$.  Удобно представить оценку $f =3\mu/2$ в следующем виде: $$\label{Eqf} f = \frac{v_0^2 a_*^2-h_0}{\xi_0^2}=\frac{v_0^2 a_*^2}{\xi_0^2}\varepsilon,\tag{11.2}$$ где $\varepsilon=1-h_0\chi_0^2/(v_0 R_*)^2$ - безразмерный параметр модели, заменяющий $h_0$. В результате для $\mu$ имеем соотношение: $$\label{Defmuf}       \mu = 2f/3=\frac{2v_0^2 R_*^2}{3\xi_0^4}\varepsilon.\tag{11.3}$$
      Важным параметром для оценивания положения звезды на диаграмме рис. 1 является величина безразмерной координаты $x_*=a_*/a_0$, где $a_0$ - значение масштабного фактора в особой точке фазовой диаграммы, которая определяется из соотношения (\ref{Eqmua}):$$\label{Defa0}a_0 = \mu/|\nu|.\tag{11.4}$$ Эта величина указывает характерный масштабный фактор (размер объекта), который звезда должна иметь, чтобы ее осцилляции совершались на фазовой диаграмме вблизи особой точки. Отсюда находим реальную безразмерную координату Солнца на фазовой диаграмме:   $$\label{Defxs} x_{*} = \frac{a_{*}}{a_0}=\frac{2\pi G R_*^2\rho(0) }{v_0^2\varepsilon}|\lambda_*|.\tag{11.5} $$
      Вторая координата $y_*$ на фазовой диаграмме рис. 1 для данной звезды должна оцениваться из (\ref{DefE}), что дает следующее соотношение: $$\label{Defy0} y_* = \sqrt{2x_*^{-1}-x_*^{-2}+2E_*},\tag{11.6}$$ где $E_*$ - энергетический параметр текущей фазовой траектории звезды. Значение параметра $E_*$ можно оценить, если известна реальная скорость изменения радиуса звезды: $$\label{Defc0}      c_*=\dot{a}=t_0 y_*/a_0\tag{11.7}$$ в текущий момент времени.
      Как следует из приведенных формул, основными параметрами, которые определяют текущую фазовую траекторию звезды являются $k,~\lambda_*,~\varepsilon$. Параметры $\gamma$ и $n$ определяются свойствами вещества звезды и для нормальных звезд равны, соответственно, $\gamma=5/3$  и $n=3/2$. Параметры же $k,~\lambda_*,~\varepsilon$ приходится оценивать с помощью сравнения свойств вычисленных модельных распределений температуры и плотности с аналогичными свойствами реальных распределений. Однако один из этих параметров можно исключить из анализа, учитывая предполагаемое положение звезды (далее Солнца) вблизи особой точки $x=1,~y=0$ на фазовой диаграмме.
     С точки зрения данной модели наличие слабых осцилляций звезды означает, что текущее значение ее безразмерной координаты $x_*$ должно почти точно совпадать со значением $1$: $x_*\simeq 1$, а величина энергетического параметра $E$ не должна сильно отличаться от $E_0=-0.5$. Выбор $x_*$ и $E_*$ должен определяться наблюдаемым размахом колебаний звезды $\Delta_E$. Исходя из этих рассуждений, для звезд в состоянии, близком к статическому равновесию параметр $\lambda_*$ можно выбрать исходя из формулы (\ref{Defxs}):$$\label{Estpde}\lambda_* \simeq - \frac{x_* v_0^2}{2\pi G R_*^2\rho(0) }\varepsilon.\tag{11.8}$$ Полагая $x_*\simeq 1$, из этого соотношения можно найти значение $\lambda_*$, которое должно обеспечивать положение звезды вблизи особой точки фазовой диаграммы.
     Полученная таким способом оценка $\lambda_*$ явно не зависит от значения параметров $n$ и $k$. Тем не менее такая зависимость существует. Оценка (\ref{Estpde}) при заданных $n$ и $k$ может оказаться больше, чем $\lambda_{cr}$.  В этом случае, как это уже обсуждалось ранее, нарушается принцип существования физически значимых значений плотности и температуры при всех значениях радиальной координаты. Таким образом, осцилляционный режим для данной конкретной звезды возможен только при некоторых подходящих значениях $n$ и $k$.
     Подходящие величины $n$ и $k$ можно определить прямыми вычислениями для $\varepsilon=1$. Поскольку по определению $0\le \varepsilon\le 1$, то при $\varepsilon=1$ находится минимальная величина $\lambda_*$, соответствующая выбранным значениям $n$ и $k$. После этого величину $\varepsilon$ можно уменьшать в диапазоне $\varepsilon_{cr}<\varepsilon<1$, где $\varepsilon_{cr}$ соответствует значению $\lambda_*=\lambda_{cr}$. Выбор конкретной величины $\varepsilon$ может осуществляться, исходя из сопоставления величин, полученных численным способом, с величинами, соответствующими конкретным параметрам структуры и эволюции звезды. Далее при построении модели Солнца в качестве критерия выбора параметра $\varepsilon$ выбираются величина ${\cal T}_{min}$ температуры в минимуме, лежащем в фотосфере, и период осцилляций $P_{E}$. В качестве вторичного признака используется величина ${\cal T}_{max}$ в следующим за ним максимуме.

12. Оценка положения Солнца на фазовой диаграмме
 
     Рассмотрим теперь оценки, которые можно получить в применении развитой модели к Солнцу. Для Солнца хорошо известны основные физические параметры, необходимые для получения относительно надежных оценок параметров модели. Стандартным предположением является то, что Солнце относится к нормальным звездам, состоящим из одноатомного газа с $\gamma=5/3$ и $n=3/2$. Также для Солнца известны значение видимого радиуса $R_{\odot}\simeq 7\cdot 10^{10} [см]$,  значение скорости зонального потока на экваторе $v_{\odot}\simeq 2\cdot 10^{5} [см/с]$ и плотность в центре, оцениваемая величиной $\rho_{\odot}\simeq 150 г/см^3$ [8].
     Как показывает численный анализ, наиболее подходящее значение параметра $k$ равно $k=-0.7$, что соответствует эффективным значениям показателя адиабаты $\gamma'=\gamma+ k/n = 6/5$ и показателя политропы $n'=5$. Этот вывод сделан, исходя из двух основных показателей. Первый состоит в том, чтобы для выбранного $k$ значение $\lambda_*$, вычисленное в соответствии с (\ref{Estpde}) для $x_*\simeq 1,~\varepsilon=1$, не оказалось больше $\lambda_{cr}$.  Вторым показателем является требование, чтобы при изменении $\varepsilon$ в диапазоне $[\varepsilon_{cr},1]$, температура ${\cal T}_{min}$ в первом минимуме и период осцилляций могли быть согласованы с реальными данными. Например, уже при $k=-0.678$ и $\varepsilon=1$ величина $\lambda_*$ (\ref{Estpde}) оказывается большим, чем $\lambda_{cr}$. При $k<-0.7$ температура $T_{min}$ и контраст между $T_{min}$ и $T_{max}$ становятся слишком маленькими по сравнению с реальными данными. Только при  $k\simeq-0.7$ удается согласовать между собой все основные критерии выбора модели, указанные в предыдущем разделе.
     Следует отметить, что в классической модели LEm ($\lambda=0$) значение $\gamma=6/5$ соответствует граничному значению показателя адиабаты, при котором распределение плотности газа оказывается монотонно убывающим с ростом $\chi$, что эквивалентно отсутствию видимого радиуса звезды [4,3]. Обычно это интерпретируется как невозможность существования устойчивого статического равновесия такой конфигурации. В рассматриваемой модели для $\lambda < \lambda_{cr}$ минимумы имеются, что соответствует не статическому, а динамическому равновесию звезды.

 12.1. Модели для различных значений $\varepsilon$ при $k=-0.7$

Для выбора подходящей модели проводились вычисления кривых распределения коэффициентов температуры ${\cal T}$, плотности ${\cal R}$ и энтропии ${\cal S}$ для значений $\varepsilon$ в диапазоне от $1$ и до величины $\varepsilon=1.0\cdot 10^{-5}$. Интервал автомодельной радиальной координаты $\chi$, на котором вычислялись параметры среды, содержал первый минимум и следующий за ним максимум ${\cal T}$. Это позволяло оценить по графикам кривых с достаточной точностью значения $\chi_0$, ${\cal T}_{min}$, ${\cal T}_{max}$. На рис. 13 представлены графики распределения коэффициента энтропии и температуры для $k=-0.7$ и $\varepsilon=1$.
     Рис. 13(a,b,c) демонстрируют общее распределение $\lg({\cal S})$(a), $\lg({\cal T})$(b) и $\lg({\cal R})$(c). На рис. 14(a,b) представлены участки общего распределения коэффициента температуры, которые иллюстрируют положения первого минимума $\chi_0$ и следующего за ним максимума $\chi_1$. Значения ${\cal T}$ в этих точках, как и раньше, обозначаются далее, соответственно, ${\cal T}_{min}={\cal T}(\chi_0)$ и  ${\cal T}_{max}={\cal T}(\chi_1)$. Для данных значений $k$ и $\varepsilon$ получаем $\lambda_*\simeq -1.297990\cdot 10^{-7}$, а также следующие оценки $\chi_0\simeq 105$, ${\cal T}_{min}\simeq 3\cdot 10^{-3}$, $\chi_1\simeq 400$ и ${\cal T}_{max}=\simeq 0.12$.
 

Рис. 13. Коэффициенты энтропии $\lg({\cal S})$ (a), температуры $\lg({\cal T})$ (b) и плотности $\lg({\cal R})$ для одноатомного газа с $n=3/2(\gamma=5/3)$ для $k=-0.7$ и $\varepsilon=1$

Рис. 14. Коэффициент температуры ${\cal T}(\chi)$ для одноатомного газа с $n=3/2(\gamma=5/3)$ для $k-0.7$ и $\varepsilon=1$ в двух диапазонах $\chi$ вблизи нуля

На рис. 15(a,b,c,d) представлены результаты вычисления $P_{E}$(a), ${\cal T}_{min}$(b), ${\cal T}_{max}$(c) и $\chi_0$(d) зависимости от $\varepsilon$ в двойном логарифмическом масштабе. Каждая точка соответствует модели с определенным значением $\varepsilon$. На диаграммах
    $P_{E}$(a), ${\cal T}_{min}$(b) серым цветом выделены области значений периодов осцилляций и температуры, наиболее согласующиеся с данными о Солнце. Эта же область выделена и на диаграмме для и ${\cal T}_{max}$(c). Как видно из диаграмм, результаты численного счета для всех параметров хорошо укладываются на прямые, соответствующие степенной зависимости от $\varepsilon$. Соответствующие зависимости аппроксимируются следующим образом: $$P_{E}(\varepsilon) \simeq P_E(1)\cdot \varepsilon^{-1/2}=0.085\cdot \varepsilon^{-1/2}\ [год],$$ $$ T_{min}(\varepsilon)\simeq T_{min}(1)\cdot \varepsilon^{1/3}=1.14\cdot 10^5\cdot \varepsilon^{1/3}\ [K],$$ $$ T_{max}(\varepsilon)\simeq T_{max}(1)\cdot \varepsilon^{1/5}=7.49\cdot 10^5\cdot \varepsilon^{1/5}\ [K],$$ $$ \chi_{0}(\varepsilon)\simeq \chi_{0}(1)\cdot \varepsilon^{-1/3}=530\cdot \varepsilon^{-1/3}.$$

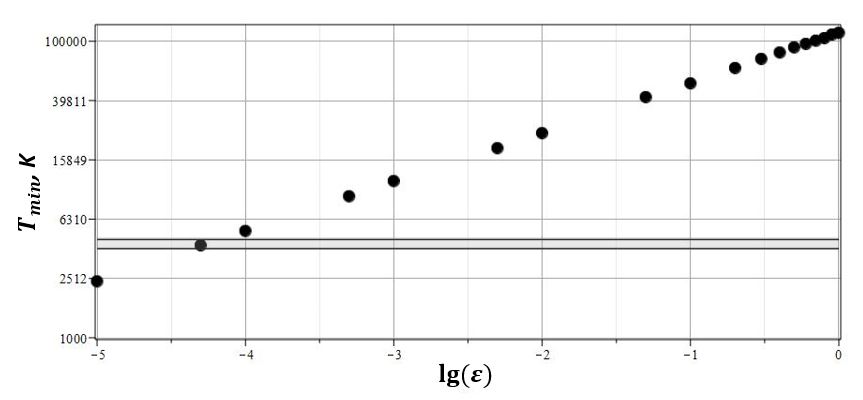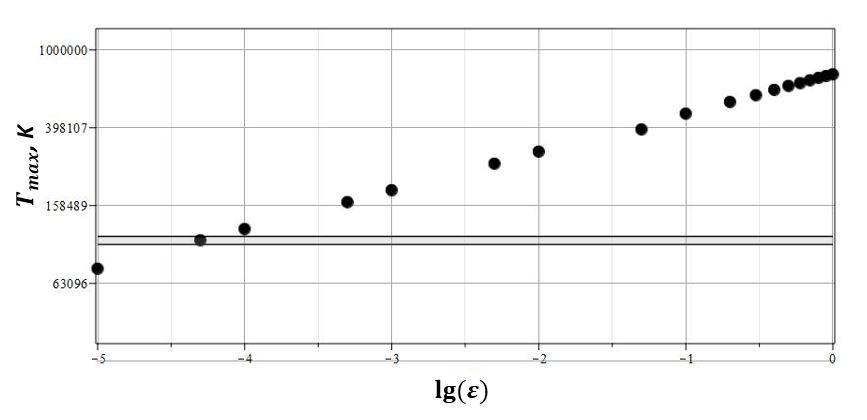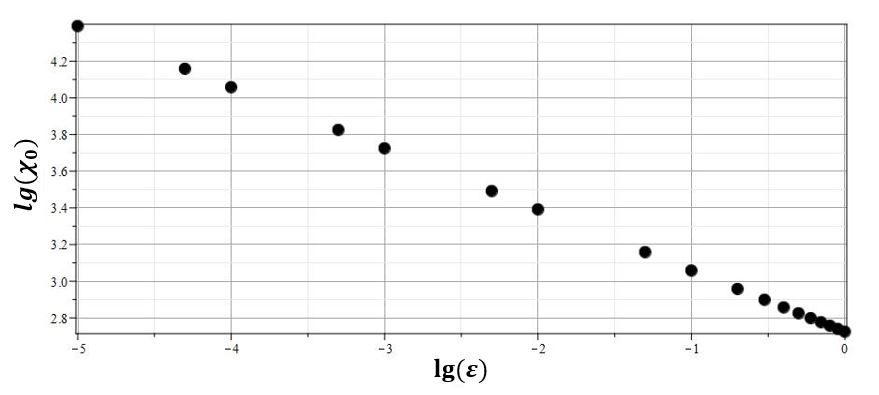Рис. 15. Зависимость параметров модели от значений параметра $\varepsilon$: $P(E)$--a, ${\cal T}_{min}$--b, ${\cal T}_{max}$--c, $\chi_0$--d.

Как следует из представленных диаграмм при $\varepsilon=0.6\cdot 10^{-4}$  период радиально-зональных осцилляций Солнца совпадает с наблюдаемым периодом солнечной активности, равным примерно 11 лет. При этом температура в минимуме фотосферы оказывается почти точно совпадающей со значением $T_{\odot}\simeq 4800 [K]$, которое дается стандартной моделью Солнца [8]. Существенным отличием от реальных данных является значение лишь значение $T_{max}$.

12.2. Пространственное распределение температуры для оптимального выбора параметров

На рис. 16 представлены $\lg({\cal S})$(a), $\lg({\cal T})$(b) и $\lg({\cal R})$(c) для $k=-0.7$ и $\varepsilon=0.6\cdot 10^{-4}$, что соответствует $\lambda_*= -7.7879456\cdot 10^{-12}$. Оставленное количество знаков после запятой в записи $\lambda_*$ необходимо, поскольку это связано с тонкой настройкой модели. Основным критерием подгонки параметра $\lambda_*$ в этой модели являлось значение безразмерного масштабного фактора $x_*$, которое должно быть максимально близким к значению $x_0=1$, соответствующему особой точке на фазовой диаграмме. Близость $x_*$ к $1$ приводит к близости значения энергетического параметра $E_*$ к значению $-0.5$, что соответствует почти нулевому размаху колебаний масштабного фактора.  Поскольку в реальности не наблюдается существенных изменений радиуса Солнца, то размах его радиальных колебаний не может существенно превышать сотню метров.
      Рис. 16(a) демонстрирует общее распределение $\lg({\cal S})$, а рис. 16(b) - $\lg({\cal T})$. Рис. 17(a,b)  служат для оценивания значений положения первого минимума $\chi_0$ и следующего за ним максимума $\chi_1$. Для данного значения $k$ и $\varepsilon$ получаем следующие оценки $\chi_0\simeq 13537$, ${\cal T}_{min}\simeq 6\cdot 10^{-3}$, $\chi_1\simeq 132000$, ${\cal T}_{max}\simeq 0.00717$. В результате для данной модели находим:  $$a_*=R_{\odot}/\chi_0\simeq 5.1710\cdot 10^6\ [см],$$ $$\label{EstP2} M_0=\rho_{\odot}a_*^{3}\simeq 2.0740\cdot 10^{22}\ [г],\tag{12.1}$$ $$\nu\simeq -7.4259\cdot 10^{8}\ [см^3/с^2],$$ $$\mu\simeq 3.8911\cdot 10^{15}\ [см^2/с]$$

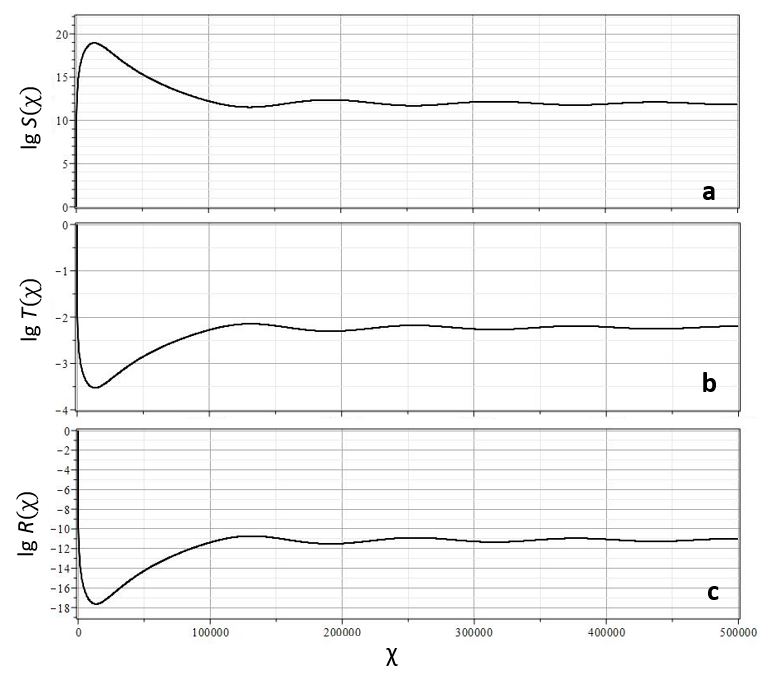Рис. 16. Коэффициенты энтропии $\lg({\cal S})$ (a), температуры $\lg({\cal T})$ (b) и плотности $\lg({\cal R})$ (c) одноатомного газа с $n=3/2(\gamma=5/3)$ для $k=-0.7$, $\varepsilon=6.0\cdot 10^{-5}$ ($\lambda_{*}\simeq -7.7879456\cdot 10^{-12}$)

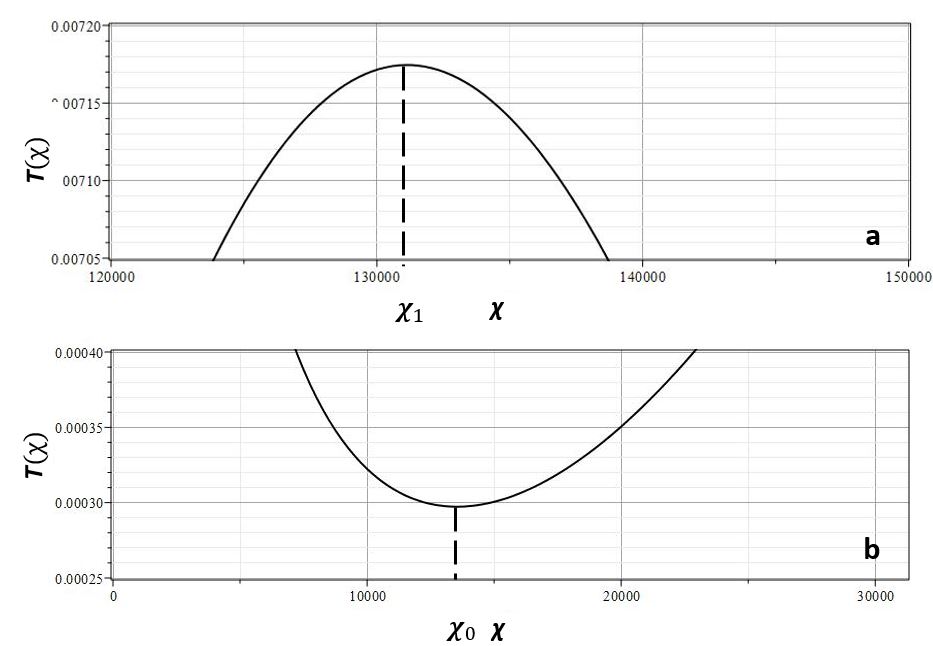Рис. 17. Коэффициент температуры ${\cal T}(\chi)$ одноатомного газа с $n=3/2(\gamma=5/3)$ для $k=-0.7$ и $\varepsilon=0.6\cdot 10^{-4}$  ($\lambda_{*}\simeq -7.7879456\cdot 10^{-12}$) в двух диапазонах $\chi$ вблизи нуля

Исходя из полученных оценок, вычисляем: $$ a_0 = \mu/|\nu|\simeq 5.7170\cdot 10^6\ [см],$$ $$ x_* =a_*/a_0 = 1-\delta x,~~\delta x\simeq 4.0\cdot 10^{-10},$$ $$\label{Estxy2} y_* \simeq 1.0\cdot 10^{-8},~~c_*\simeq 0.9\cdot 10^{-9} [см/с]\tag{12.2}$$ $$ E_*= -0.5 + \delta E,~~\delta E \simeq 5.0\cdot 10^{-15},$$ $$ \Delta_E(E_*)\simeq 2\cdot 10^{-7},~~\delta H\simeq 0.14 [км],$$ $$ P(E_*) \simeq 11.03 [год]$$ Параметр $E_*$ вычислялся по условию обращения $y_*$ в ноль с требуемой точностью.
     Из оценки величины $x_*$ следует, что данная модель описывает колебательный режим вблизи особой точки $x_0=1$ с периодом около $11$ лет. Для данного значения $\varepsilon\simeq 6.0\cdot 10^{-5}$ и заданном значении $x_*$ и $E_*$ величина размаха оценивается величиной $\delta H\simeq 0.14 [км]$ со средней скоростью перемещения поверхности $c = \delta H/P\simeq 1.3\cdot 10^{-2}\ [км/год]$ будет маленькой величиной, которую трудно обнаружить на фоне флуктуаций и волновых колебаний плазмы вблизи поверхности Солнца.
      Анализируя распределение ${\cal T}$, соответствующее данной модели в предположении, что температура в центре Солнца $T_{\odot}\simeq 15\cdot 10^6 [K]$, находим, что в минимуме фотосферы температура $T_{min}\simeq 4500 [K]$ вполне соответствует реально наблюдаемому значению $T_{\odot}\simeq 4800 [K]$ . Однако в следующем максимуме $T_{max}\simeq 1.01\cdot 10^{5} [K]$, что примерно в двадцать раз меньше, чем реальная максимальная температура в короне Солнца, равная по оценкам [30] $2\cdot 10^6 [K]$. При условии, что в центре Солнца $\rho(0)\simeq 150 [г/см^3]$, оценки плотности среды по численным расчетам в минимуме фотосферы равна  $\rho_{min}\simeq 1.8 \cdot 10^{-17} [г/см^3]$ и в максимуме $\rho_{min}\simeq 4.8 \cdot 10^{-11} [г/см^3]$. Эти оценки существенно ниже тех, что дает стандартная модель Солнца [8] величиной $\rho_{ph}\simeq 2.0\cdot 10^{-7}\ [г/см^3]$. Также устанавливаем, что отношение $\chi_1/\chi_0=R_{max}/R_{\odot}\simeq 9.8$ достаточно велико. Однако эта величина укладывается в общую приближенную оценку расположения максимума температуры в короне Солнца в несколько его радиусов [8].  Таким образом, можно констатировать, требуется определенная модификация модели  для более детального согласования ее модели с реальными данными. Для этого в первую очередь следует  использовать более точные соотношения для энтропии (\ref{DefS}), в частности, вводя в расчеты подходящую зависимость ${\cal H}_0={\cal H}_0(\chi)$, а также учитывать процессы излучения и влияние магнитного поля. В частности, существенное отличие температуры $T_{max}$ от реально наблюдаемого значения $\simeq 2\cdot 10^6 [K]$, возможно, связано с не рассматриваемыми в данной работе процессами турбулентности и диссипации различного рода магнитоактивных волн в короне Солнца [35].

13. Заключение

В работе развита теория динамического равновесия пространственного распределения самогравитирующего газа, обладающего цилиндрической симметрией с автомодельной эволюцией его параметров со временем. Такой тип равновесия определяется специфическим типом взимодействия радиального гидродинамического потока газа - потоком Хаббла и зональным потоком, который лишь частично связан с вращением звезды  как твердого тела. Как показано в данной работе, именно наличие взаимодействия радиального и зонального потоков позволяет существовать режиму осцилляций звезд. Фактически режим осцилляций связан с периодическим преобразованием энергии радиального расширения звезд в энергию зонального потока и в потенциальную энергию гравитационного поля и обратно. Как отмечалось в разделе 17, модель зонального потока, хотя формально и не имеет особенностей, но приводит к особенностям в потенциале на оси вращения. Поэтому данная модель требует в дальнейшем уточнения для устранения этой особенности.
     В работе выведены уравнения автомодельных осцилляций и показана их связь с параметром динамического равновесия $\lambda$, появление которого в теории обеспечивается и потоком Хаббла [12], и зональным потоком. Этот параметр является критерием отклонения суммарного значения сил Архимеда и тяготения в ту или иную сторону в зависимости от знака $\lambda$, что приводит к ускорению или замедлению радиального расширения звезды и ее зонального потока.  Модели осцилляций связаны с отрицательным значением параметра $\lambda$. С этой точки зрения в данной работе получены условия возникновения осцилляций, которые оценены для модели с различными параметрами в сопоставлении с данными о Солнце. В данной работе одним из важных аспектов, связанным с моделями осцилляций, является вывод соотношения период-светимость для осцилляций в аналитической безразмерной форме. Форма полученной кривой совпадает качественно с известными кривыми период-светимость для цефеид. Это дает основания надеяться, что данная модель может быть использована в теории звездных пульсаций для звезд на различных стадиях эволюции.
     С точки зрения пространственного распределения плотности и температуры построенные и исследованные модели представляют собой модифицированные модели mLEm, содержащие ключевой дополнительный параметр динамического равновесия $\lambda$, отсутствующий в классических уравнениях теории Лейна-Эмдена.  Все такие модели  распадаются на три основных класса по диапазону, в котором принимает значение параметр динамического равновесия $\lambda$. Границы диапазонов определяются значениями $\lambda=\lambda_{cr} < 0$ и $\lambda=-1$. В диапазоне $[\lambda_{cr},\infty)$ лежат модели, для которых коэффициенты плотности и температуры хотя бы при одном значении автомодельного радиуса обращаются в ноль. Для $\lambda=\lambda_{cr}$ имеется только одна точка, в которой плотность обращается в ноль. Эти модели являются наиболее близкой модификацией классических моделей Лейна\,--\,Эмдена, которым соответствует значение $\lambda=0$. Формально, как это и делается в классической теории статического равновесия, модели с $\lambda > \lambda_{cr}$ могут рассматриваться как модели звезд в ограниченной области радиальной координаты вблизи центра. В отличие от классических моделей LEm модифицированные модели, в том числе и при $\lambda=0$, оказываются нестатическими и их динамика описывается автомодельными решениями уравнений модели mLEm.
      Модели с $\lambda_{cr} > \lambda > -\infty $ (за исключением $\lambda=-1$) описывают пространственные осцилляции плотности и температуры, амплитуда которых убывает при $r\to\infty$. Предельное значение температуры и плотности на бесконечности зависит от значений $\lambda$, $\gamma$ и параметров пространственного распределения энтропии. Модели с $\lambda=-1$ при однородном или политропном распределении энтропии в независимости от показателя адиабаты газа $\gamma$ приводят к однородному пространственному распределению плотности и температуры. Все такие модели при определенных условиях могут иметь режим осцилляций по времени. Как отмечалось в выше, на больших расстояниях от центра плотность газа в моделях с $\lambda <0$ стремится к некоторому постоянному значению $\rho_{\infty}$. Поэтому такие модели с физической точки зрения имеет смысл рассматривать только до границы астросферы (гелиосферы для Солнца), на которой происходит взаимодействие солнечного ветра и межзвездной среды.
      Важным элементом данной модели, делающей ее пригодной для описания  реальных звезд, является модель квазиполитропного распределения энтропии в звездах, соответствующая (\ref{DefS}). Это соотношение превращает модель mLEm общего вида в модель с политропным процессом эволюции звезд с показателем политропы, отличающимся от классического случая с адиабатическим процессом эволюции. В работе анализировались модели с чисто политропным распределением энтропии, что соответствует ${\cal H}_0(\chi)=1$. Как было показано, в таких моделях распределение потоков тепла модифицирует термодинамические параметры среды, превращая ее в среду с эффективным показателем политропы, отличающимся от показателя политропы самого газа. Это позволяет построить модель Солнца, согласующуюся с реальными данными по основным параметрам ее структуры и эволюции. В частности, показано, что в случае распределения энтропии c $k=-0.7$, приводящем к эффективному показателю адиабаты $\gamma=6/5$, параметры модели при подходящем выборе параметра зонального потока $\varepsilon=6.0\cdot 10^{-5}$ дают период осцилляций Солнца вблизи значения $11.3$ года при температуре в минимуме фотосферы, равной $4500 K$. Эти параметры очень близки к реально наблюдаемым параметрам 11-летнего цикла солнечной активности. Поскольку все модели с $\lambda_{cr} > \lambda > -1 $ описывают пространственные осцилляции температуры и плотности вне звезды, то наличие таких осцилляций объясняет простым образом наличие максимума температуры в короне Солнца. Но для чисто политропного распределения энтропии, которое анализировалось в данной работе, величина максимума температуры в короне Солнца при оптимальном выборе других параметров примерно в двадцать раз меньше реально наблюдаемого значения для Солнца, равного $\simeq 2\cdot 10^6\ [K]$, и имеет значение $T_{max}\simeq 100000\ [K]$. По всей видимости, это расхождение можно устранить с помощью уточнения модели, включив в нее подходящий множитель ${\cal H}_0(\chi)$ неполитропного характера.
     Решения с $\lambda \le -1$ могут использоваться в качестве моделей динамики газа после их взрыва, когда почти вся масса газа выбрасывается наружу. Эти модели в некотором смысле можно рассматривать как космологические, в особенности, модель с $\lambda=-1$. Последняя модель, по сути, представляет модель расширения газа с однородным распределением плотности, что характерно для моделей с пылью.
      Рассмотренные модели не учитывают ряд важных факторов реальной динамики и строения звезд, например, такие, как наличие магнитного поля, изменения тепловыделения за счет ядерных реакций и возможной неавтомодельности теплопередачи в газе. Модель не учитывает, например, охлаждение газа за счет излучения в области пространственных осцилляций. Кроме этого, в работе рассматривалось лишь сферически-симметричное приближение к пространственному распределению плотности и температуры. Для меридианальных составляющих таких распределений были лишь выписаны сами уравнения без прямого анализа их решений. Этот анализ не проводился  из-за ограниченности объема одной статьи. Анализ и учет всех дополнительных факторов требует усложнения представленных моделей. Эти уточнения могут дать более адекватное согласие с реальными данными о строении звезд.

 14. Приложение

Разделение переменных в уравнении (\ref{EqPhi}) приводит к следующему соотношению: $$ \frac{2\pi G M_0}{a}\left(\frac{1}{\xi}\frac{\partial}{\partial \xi}\left(\xi\frac{\partial\Phi_0}{\partial \xi}\right)+\frac{1}{\beta}\frac{\partial^2}{\partial \zeta^2}\Phi_0\right)+\frac{1}{a^2}\left(\frac{\mu}{\beta}+\frac{1}{\xi}\frac{\partial}{\partial \xi}(\xi n)\right)=0.$$ Отсюда следует, что функция $\Phi_0$ удовлетворяет уравнению: $$\label{EqPhi0}\frac{1}{\xi}\frac{\partial}{\partial \xi}\left(\xi\frac{\partial\Phi_0}{\partial \xi}\right)+\frac{1}{\beta}\frac{\partial^2}{\partial \zeta^2}\Phi_0=0,\tag{A1}$$  а функция $n(\xi)$ принимает следующий вид: $$\label{Defn}n = -\frac{\mu\xi^2}{4}-h_0\ln\xi -C_1.\tag{A2}$$   Учитывая связь (\ref{VarPG1}) между $h$ и $n$, находим: $$\label{Defh}h = \frac{\mu}{2}\xi^4+h_0\xi^2.\tag{A3}$$ Отсюда следует: $$\label{DefVP}V^2 = f \xi^4 + h_0 \xi^2.\tag{A4}   $$ где $f = 3\mu/2$. Вспомогательный потенциал $\Phi$ теперь имеет такой вид: $$\Phi = \frac{2\pi G M_0}{a}\Phi_0 + \frac{\beta^2 \mu}{2a^2}\zeta^2- \frac{1}{a^2}\left(\frac{\mu\xi^2}{4}+h_0\ln\xi +C_1\right).$$ Слагаемое с $\ln\xi$ имеет сингулярность в нуле, что указывает на необходимость уточнения модели вблизи оси вращения звезды.

Список литературы

[1] Я.~Б.~Зельдович, И.~Д.~Новиков. {\it Теория тяготения и эволюция звезд.} Наука, Москва (1971)

[2] В.~Г.~Горбацкий. {\it Космическая газодинамика.} Наука, Москва (1977)

[3] Я.~Б.~Зельдович, С.~И.~Блинников, Н.~И.~Шакура. {\it Физические основы строения и эволюции звезд.} Изд. МГУ, Москва (1981)

[4] С.~Вайнберг. {\it Гравитация и космология.}  Мир, Москва (1975)

[5] Я.~Б.~Зельдович, И.~Д.~Новиков. {\it Строение и эволюция Вселенной.} Наука, Москва (1975)

[6] О.~И.~Богоявленский {\it Методы качественной теории динамических систем в астрофизике и газовой динамике}. M.: Наука, (1980)

[7] В.~Г.~Бисноватый-Коган. {\it Физические вопросы звездной эволюции.} М.: Наука, (1989)

[8] {\it Плазменная гелиофизика}. {\bf 1} Под ред. Л.М. Зеленого, И.О. Веселовского. M.: ФИЗМАТЛИТ, (2008)

[9] Дж.~П.~Кокс. {\it Теория звездных пульсаций}, М.: Мир (1983)

[10] J.~R.~Bucher, arXiv: 0907.1766v1 (2009)
% The State of Cepheid Pulsation Theory

[11] А.~С.~Расторгуев Звездные маяки Вселенной. М: ГАИШ, http://lnfm1.sai.msu.ru/~rastor (2015)

[12] В.~М.~Журавлев, Пространство, время и фундаментальные взаимодействия, N4, 10, (2020)

[13] D.~K.~Nadezhin, Soviet physics - astronomy, {\bf 12}, N 6, 924 (1969)

[14] R.~A.~Chevalier, E.~A.~Lufkin, Astrophysical Journal, {\bf 356}, 41 (1990)

[15] M.~V.~Murzina, D.~K.~Nadezhin, Astron. Zh, {\bf 68} 574 (1991)

[16] Ue-Li Pen, Astrophysical Journal, {\bf 429}, 759 (1994)

[17] R.~N.~Antonova, Ya.~M.~Kazhdan, Astronomy Letters, {\bf 26}, N 6, 344 (2000)

[18] J.~H.~Lane,  American Journal of Science and Arts, Second Series, 50, 57 (1870) %57-74.

[19] R.~Emden, Gaskugeln. B.G. Teubner, Leipzig (1907)

[20] В.~М. Журавлев.  Сб. Инновационные технологии, Ульяновск, УлГУ, 77 (2010) %Точные решения гидродинамики сжимаемой жидкости и функциональные подстановки Коула-Хопфа. C.77-93

[21] В.~М.~Журавлев. {\it Нелинейные интегрируемые модели физических процессов. Метод функциональных подстановок.} Издательство УлГУ, Ульяновск (2020)

[22] В.~М.~Журавлев, Пространство, время и фундаментальные взаимодействия,  N1, 5 (2017).

[23] В.~М.~Журавлев, ЖЭТФ, {\bf 152}, 495 (2017)

[24] V.~M.~Zhuravlev, Gravitation and Cosmology, {\bf 17}, No. 3, 201 (2011) %A topological interpretation of quantum %theory and elementary particle structure.  pp. 201–217

[25] Zhuravlev V.M. Induction Equations for Fundamental Fields and Dark Matter. \textit{Gravitation and Cosmology}, 2017, Vol. 23, No. 2, pp. 95–104 (2017)

[26] V.~M.~Zhuravlev, Gravitation and Cosmology, {\bf 28}, No. 4, (принята в печать) (2022)

[27] W.~McCrea, E.~MilneQuart. J. Math., N.5, 73 (1934)

 [28] Л.~М.~Озерной,  О.~Ф.~Прилуцкий, И.~Л.~Розенталь. {\it Астрофизика высоких энергий}. M.: Атомиздат, (1973)

 [29] В.~А.~Рубаков, Д.~С.~Горбунов. {\it Введение в теорию ранней Вселенной. Космологические возмущения. Инфляционная теория.} M.: Едиториал УРСС, (2009)

[30] M.~J.~Aschwanden. {\it Physics of the Solar Corona: an Introduction with Problems and Solutions}. Springer, Berlin (2006)

[31] A.~Genova, E.~Mazarico, S.~Goossens, F.~G.~Lemoine, G.~A.~Neumann, D.~E.~Smith, M.~T.~Zuber. Nature Communications, (2018), DOI: 10.1038/s41467-017-02558-1.

[32] С.~А.~Жевакин, Астрон. журн., {\bf 30}, 161-179 (1953)

[33] С.~А.~Жевакин, Астрон. журн. {\bf 31}, 141-153 (1954)

[34] S.~A.~Zhevakin S.A., Annual Review of Astron. and Astrophys. {\bf 1}, 367-400. (1963)

[35] J.~Squire, R.~Meyrand, M.~W.~Kunz, et al.
%High-frequency heating of the solar wind triggered by low-frequency turbulence.
Nat Astron (2022) https://doi.org/10.1038/s41550-022-01624-z

[36]  Журавлев В.М. Геометрия, топология и физические поля (Часть I). \textit{Пространство, время и фундаментальные взаимодействия}, 2014, вып. 4. С. 6-24.

[37]  Журавлев В.М. Геометрия, топология и физические поля. (Часть II). Масса и гравитация, \textit{Пространство, время и фундаментальные взаимодействия}. - 2014,-вып. 4. С. 25-39.

[38]  Журавлев В.М. Геометрия, топология и физические поля. (Часть III).   Уравнение индукции фундаментальных полей. \textit{Пространство, время и фундаментальные взаимодействия}.-2015 - N3-С. 44-60.

[39]  Журавлев В.М. Геометрия, топология и физические поля. ((Часть IV). Топологическая структура элементарных частиц. \textit{Пространство, время и фундаментальные взаимодействия}. -2015.-N4-С. 104-118.

[40] Журавлев В.М. Динамическое равновесие астрофизических объектов. ЖЭТФ, 2022