Ньютон находил задачу движения Луны настолько трудной, что, как он жаловался, она вызывала у него головную боль, лишала сна и он больше не мог о ней думать. Однако ему удалось показать, что известные неравенства в орбитальном движении Луны вызваны Солнцем. Кроме того, учитывая члены второго порядка, он вычислил движение перигея, отличающееся от наблюдаемого значения всего на 8%. [1]. Непросто вычислить и движение лунного узла. По крайней мере, мне не доводилось видеть простой формулы для  скорости прецессии лунного узла.

                Известно, что плоскость лунной орбиты поворачивается как крышка от кастрюли, упавшая на пол. При этом точки пересечения орбиты Луны с плоскостью эклиптики бегают по кругу, совершая полный оборот за 18.6 лет. Такое движение называют прецессионным. А можно ли вычислить период прецессии лунной орбиты, уподобив ее крышке? Давайте попробуем.

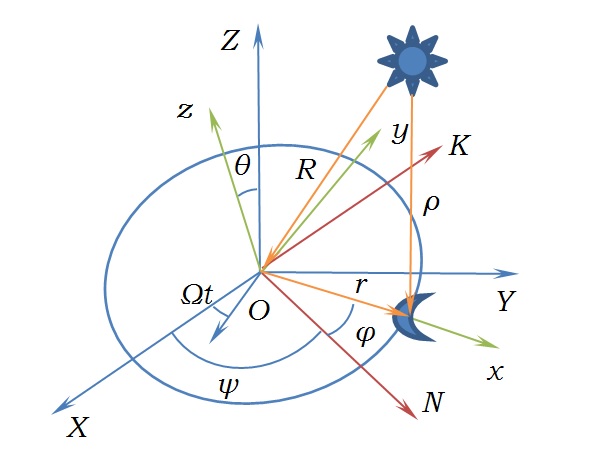
        Рассмотрим три системы координат. Пусть OXYZ –неподвижная система координат с началом в центре Земли. Оxyz - подвижная система координат, вращающаяся с постоянной угловой скоростью $\omega$ и в которой Луна имеет неизменные координаты (r,0,0). ONKz – подвижная система координат, скорость триэдра которой отличается от $\omega$ и задается следующими проекциями [2]:

$(\dot\theta, \dot\psi\sin\theta, \dot\psi\cos\theta)$             (1)

Орбитальный кинетический момент Луны достаточно велик, чтобы пренебречь двумя из его проекций, и рассматривать только одну составляющую, ортогональную плоскости лунной орбиты.

Это позволит нам записать уравнения движения Луны без вторых производных эйлеровых углов [3]:

$\\\dot\psi=\frac{M_N}{C\omega\sin\theta} \\\dot\theta=-\frac{M_K}{C\omega}\\\dot\omega=\frac{M_z}{C}$     (2)

где $C=m r^2$- орбитальный момент инерции Луны,   m – масса Луны, r – расстояние от Земли до Луны.

Теперь нам нужно найти проекцию момента силы гравитации Солнца на линию узлов ON.

Момент силы, действующей на Луну равен:

$\boldsymbol{M}=-\frac{\lambda m}{\rho^3}(\boldsymbol{r}\times \boldsymbol{\rho})$       (3)

где  $\lambda$ - гравитационный параметр Солнца, $\rho$ - расстояние от Солнца до Луны. 

Орбиту Луны считаем круговой. Предполагаем, что «орбита» Солнца не отличается от окружности.

Тогда координаты Солнца в неподвижной системе координат равны:

$ \\X=-R\cos\Omega t\\Y=-R\sin\Omega t\\Z=0$           (4)

Перечислим элементы матрицы поворота $A$, связывающей системы OXYZ и ONKz:

$\\a_{11}=\cos\psi \\a_{12}= - \sin\psi \cos\theta \\a_{13} =\sin\psi \sin\theta \\a_{21}=\sin\psi\\a_{22} =\cos\psi \cos\theta \\a_{23}= - \cos\psi \sin\theta \\a_{31}= 0 \\a_{32} =\sin\theta \\a_{33}= \cos\theta$        (5)

Обратная ей матрица получается транспонированием. Именно она нужна нам, чтобы получить координаты векторов в системе ONKz. Во избежание путаницы, индексы элементов мы будем использовать те, которые они имеют в «прямой» матрице.

Радиус вектор Луны является суммой двух векторов:

$\boldsymbol{\rho}=\boldsymbol{R}+\boldsymbol{r}$     (6)

А его модуль равен:

$\rho=(R^2+r^2+2\boldsymbol{R}\cdot \boldsymbol{r})^{1/2}=R \left( 1+\frac{2\boldsymbol{R}\cdot \boldsymbol{r}}{R^2}+\frac{r^2}{R^2}\right)^{1/2}$     (7)

В случае с Луной величиной $\frac{r^2}{R^2}$ можно пожертвовать.

Тогда

$\frac{1}{\rho^3}=\frac{1}{R^3}\left(1-3\frac{\boldsymbol{R}\cdot \boldsymbol{r}}{R^2}\right)$         (8)

Вспомним, что векторное произведение вектора самого на себя равно нулю:

$\boldsymbol{r}\times\boldsymbol{\rho}=\boldsymbol{r}\times(\boldsymbol{R}+\boldsymbol{r})=\boldsymbol{r}\times\boldsymbol{R}$                (9)

Результирующий момент теперь можно представить как сумму двух моментов:

$\boldsymbol{M_1}=-\frac{\lambda m}{R^3}(\boldsymbol{r}\times\boldsymbol{R})$     (10)

$\boldsymbol{M_2}=\frac{3\lambda m}{R^5} (\boldsymbol{r}\times\boldsymbol{R})(\boldsymbol{r}\cdot \boldsymbol{R})$                (11)

Запишем координаты вектора $\boldsymbol{R}$ в системе ONKz:

$(R_N, R_K, R_z )=A^T (R_X, R_Y, R_Z) $          (12)

Откуда:

$\\R_N=R_X a_{11}+R_Y a_{21}\\ R_K=R_X a_{12}+R_Y a_{22}\\R_z=R_X a_{13}+R_Y a_{23}$               (13)

Запишем координаты вектора $\boldsymbol{r}$ в системе ONKz:

$\\r_N=r\cos\varphi\\ r_K=r\sin\varphi \\r_z=0$           (14)

Распишем векторное произведение:

$\boldsymbol{r}\times \boldsymbol{R}=(rR_z\sin\varphi,-rR_z\cos\varphi,rR_K\cos\varphi-rR_N\sin\varphi)$ (15)

Теперь распишем скалярное произведение:

$\boldsymbol{r}\cdot \boldsymbol{R}=r R_N\cos\varphi+rR_K\sin\varphi$       (16)

Аккуратно перемножив все синусы и косинусы, получим:

$M_{1N}=\frac{\lambda m r}{R^2}\sin(\psi-\Omega t)\sin\theta\sin\varphi$        (17)

При осреднении данное выражение обращается в ноль. Таким образом, нас будет интересовать только момент $\boldsymbol{M_2}$

Проанализируем выражение для координаты N вектора, полученного премножениием векторного и скалярного произведения $(\boldsymbol{r}\times\boldsymbol{R})(\boldsymbol{r}\cdot \boldsymbol{R})$:

$(\boldsymbol{r}\times\boldsymbol{R})(\boldsymbol{r}\cdot \boldsymbol{R})_N=r^2\sin\varphi\cos\varphi R_N R_z+r^2\sin^2\varphi R_K R_z$               (18)

Произведение $R_N R_z$ содержит только первые степени тригонометрических функций, в отличие $R_K R_z$, которое содержит вторую степень:

$R_K R_z=-R^2\sin\theta\cos\theta\sin^2(\psi-\Omega t)$     (19)

Таким образом, среднее значение проекции солнечного гравитационного момента на линию узлов равно:

$ \overline{M_{2N}}=-\frac{3\lambda m r^2\sin\theta\cos\theta }{R^3}\overline{sin^2(\psi-\Omega t)sin^2\varphi}$                                                        (20)

Соответственно, средняя скорость прецессии лунного узла равна:

$\overline{\dot\psi}=-\frac{3\lambda \cos\theta }{\omega R^3}\overline{sin^2(\psi-\Omega t)sin^2\varphi} $ (21)

Если пренебречь  сдвигом лунного узла за период осреднения в один год и, учитывая, что $\frac{\lambda}{R^3}=\Omega^2$ получим:

$\overline{\dot\psi}=-\frac{3 }{4 }\frac{\Omega^2}{\omega}\cos\theta$          (22)

К сожалению, мы не можем пренебречь сдвигом лунного узла за период осреднения и нам напоследок придется решить трансцендентное уравнение, заменив $\psi$ на $\overline{\dot\psi} t$

В итоге среднее значение выражения под чертой будет равно не 0.25, а 0.24.

Подставив справочные значения, получим скорость прецессии лунного узла:

$\overline{\dot\psi}=-3\cdot 0.24\frac{\Omega^2}{\omega}\cos\theta =-1.068\cdot10^{-8}$  (23)

что соответствует периоду обращения 18.6 лет. Неплохо!

Литература.

1.А. Рой. Движение по орбитам. Издательство «Мир» Москва, 1981.

2. Виттенбург Й. Динамика систем твердых тел. Монография. – М.: Мир, 1980.

3. Николаи Е. Л., Теория гироскопов, Л. — М., 1948.