Данная статья выражает личную точку зрения автора и опубликована самостоятельно в личном блоге.
Рассмотрим движение тела в двух системах отсчета - вращающейся (ВСО) с осями x и y и неподвижной с осями X и Y (Рис 1.)
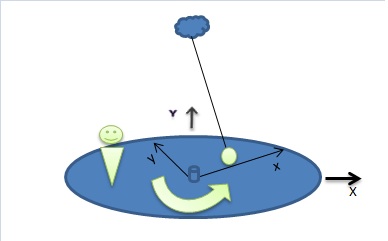
Рис. 1.
Допустим, что скорость вращения постоянна и равна Ω. Тогда угол между осями координат подвижной и неподвижной системы изменяется по закону θ=Ωt
Траектория тела в абсолютной и неподвижной системе отсчета связана с его траекторией во вращающейся системе следующими соотношениями:
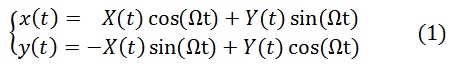
Или в комплексной форме :
.jpg)
где z=x+iy, Z=X+iY
или в матричной форме, опуская скобки (t) и (Ωt)
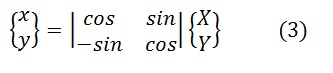
Обозначим матрицу поворота буквой С, а обратную ей С -1. Тогда
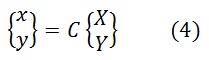
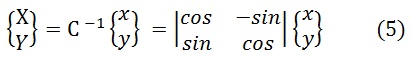
Или в комплексной форме
.jpg)
Теперь зная траекторию тела в неподвижной системе, мы можем представить, как она выглядит с точки зрения наблюдателя, вращающегося вместе с подвижной системой отсчета. Для примера возьмем математический маятник, подвешенный над вращающейся платформой, но не связанный с ней. Его траектория в неподвижной системе - отрезок прямой линии, а координаты изменяются во времени по закону:
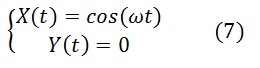
Подставляя (3) в (1) получим:
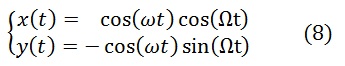
или в комплексной форме, учитывая, что cos(ωt)=0.5(eiωt+e-iωt ) ,
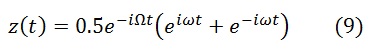
Посмотрим, как будет выглядеть траектория (8) (Рис. 2). Пусть ω=1, Ω=0.1
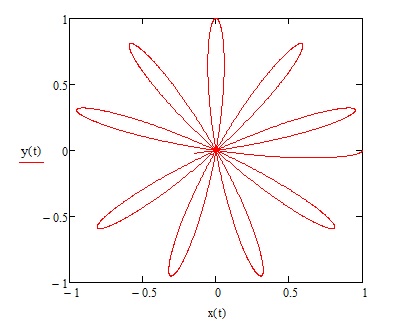
Рис. 2.
Траектория не связанного с ВСО тела в глазах наблюдателя, находящегося в ВСО, напоминает ромашку. Поворот траектории (прецессия) происходит ПО часовой стрелке, поскольку платформа вращается ПРОТИВ часовой стрелки.
Продифференцировав дважды формулу (2) установим связь между ускорениями (силами) наблюдаемыми в ВСО и реально существующими в неподвижной системе отсчета.
Относительная скорость тела связана с абсолютной формулой:
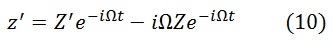
Или в матричной форме
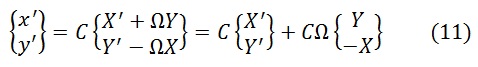
Относительное ускорение тела векторно связано с абсолютным, кориолисовым и центростремительным ускорениями.
.jpg)
Или в матричной форме
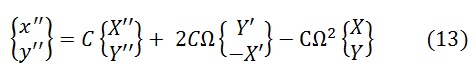
Чтобы не смущала смена знаков при переходе от комплексной к матричной форме записи, в сноске[I] приведем подробный вывод формул.
Обратите внимание! Тело движется НАД ВСО и не связано с ней, а подвижный наблюдатель может только гадать о характере сил действующих на тело в неподвижной системе отсчета.
Связь между относительными и абсолютными движениями мы получили (13), но для решения системы дифференциальных уравнений нам нужно рассматривать все соотношения в одной системе отсчета - вращающейся.
Для этого пойдем от обратного – от неподвижной системы.
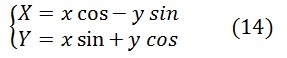
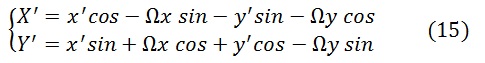
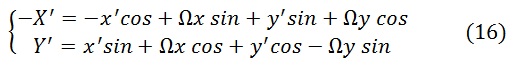
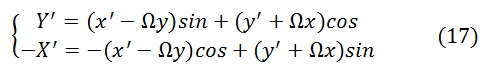
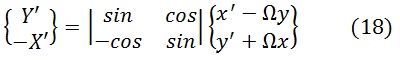
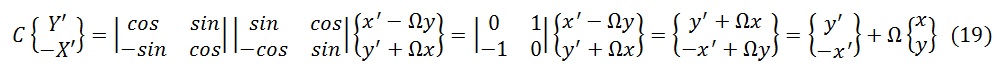
Снова обратимся к формуле (13)
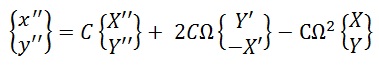
Мы уже знаем , что .jpg) , а выше получили выражение (19) для «кориолисовой части»
, а выше получили выражение (19) для «кориолисовой части»
формулы (13):
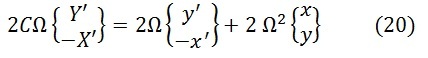
Подставляя эти соотношения в (13) придем к записи относительных ускорений в таком виде:
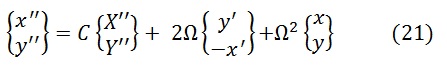
Наблюдатель во вращающейся лаборатории в расчетах должен учитывать центростремительное и кориолисово ускорение тела НЕ ЗАВИСИМО ОТ НАЛИЧИЯ СВЯЗИ ТЕЛА И ЛАБОРАТОРИИ!
Наличие и характер СВЯЗИ определяется видом первого слагаемого в выражении (21).
Мы уже близки к развязке. Для маятника в линейном приближении 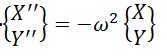
Откуда, с учетом (4),
.jpg)
Вот и готовы уравнения движения тела во вращающейся системе отсчета.
В классических учебниках можно встретить следующие (23) уравнения движения маятника на вращающейся платформе – маятника Фуко[1],[2].
В них не учитывается центростремительное ускорение, поскольку Земля вращается очень медленно по сравнению с периодом колебаний маятника.
Решением системы дифференциальных уравнений
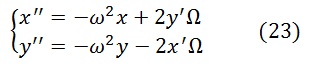
преобразованной в комплексную форму заменой z=x+iy является комплексная функция времени
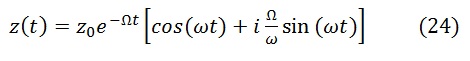
или в вещественной форме:
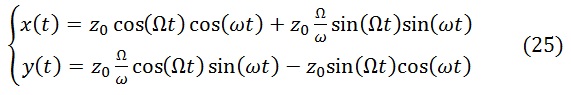
Такой вид функции получается, если начальная радиальная скорость равна нулю.
Допустим, ω=1, Ω=0.1, z0 =1+0i. Траектория движения тела под действием сил, описанных системой уравнений (23) представлена на Рис. 3:
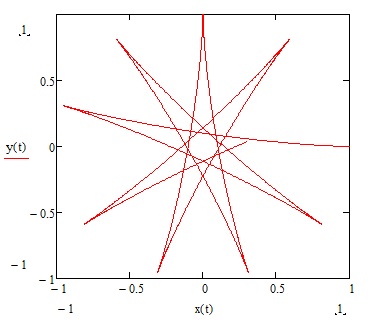
Рис.3
Траектория напоминает звезду и раскручивается по часовой стрелке. Но в какую сторону вращается платформа? Конечно же против часовой стрелки. Направление вращения определяется направлением псевдовектора Ω, который в данном случае сонаправлен оси z, образующей с осями x и y правую систему.
А теперь подвесим маятник на рамке, вращающейся вместе с платформой (Рис. 4).
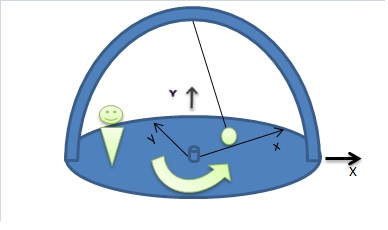
Рис. 4.
Если точка подвеса совпадает с осью вращения платформы, центробежная сила не будет действовать на маятник. Возможно, это не всем покажется очевидным. Грузик на нити, освобожденный над некоторой периферийной точкой уже раскрученной платформы, в неподвижной системе будет совершать движение обычного сферического маятника, запущенного с начальной тангенциальной скоростью 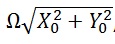 , т.е. колебания с поворотом (прецессией) траектории («эллипса»). Направление прецессии определяется направлением скорости в начальный момент времени, т.е. совпадает с направлением вращения платформы. Скорость самопрецессии траектории можно оценить по формуле
, т.е. колебания с поворотом (прецессией) траектории («эллипса»). Направление прецессии определяется направлением скорости в начальный момент времени, т.е. совпадает с направлением вращения платформы. Скорость самопрецессии траектории можно оценить по формуле
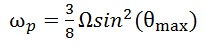 или точнее[3]
или точнее[3] 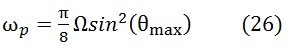
где θmax - начальный угол отклонения маятника от вертикали.
Траектория сферического маятника хорошо известна. Ее проекция на плоскость это все та же «ромашка» (Рис 5), (параметры движения: Ω=0.1, θmax =π/6 ). Только прецессия существенно меньше частоты вращения платформы и примерно равна 0.1 Ω.
.jpg)
Рис. 5.
Как эта ромашка выглядит с точки зрения наблюдателя вращающегося вместе с платформой легко представить, выполнив привычные уже преобразование координат (4) : .jpg) .
.
Естественно возникает вопрос, а как выглядит «вращающаяся звезда» в неподвижной системе отсчета. Для этого у нас есть мощный инструмент – формулы преобразования при повороте системы координат.
Особенно наглядно преобразуются координаты в комплексной форме записи:
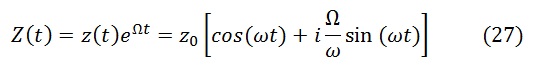
Формула (27) показывает, что «звезда» маятника Фуко в неподвижной системе выглядит как
эллипс с осями z0 и z0Ω/ω, Рис.6. Именно такой была бы траектория сферического маятника с небольшим закручиванием вокруг вертикальной оси без учета самопрецессии[4].
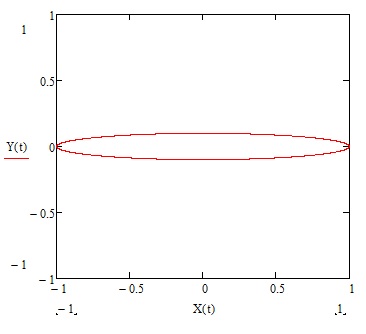
Рис. 6.
Из всего сказанного следует, что траектория сферического маятника на вращающейся платформе может быть найдена простым преобразованием координат, полученных решением дифференциальных уравнений в неподвижной системе, не используя понятия "Кориолисово ускорение", которое является побочным математическим эффектом преобразования координат из вращающейся в неподвижную систему.
[1] Ландау, Л. Д., Лифшиц, Е. М. Механика. — Издание 4-е, исправленное. — М.: Наука, 1988. — 215 с. — («Теоретическая физика», том I). — ISBN 5-02-013850-9
[2] Арнольд В. И. Математические методы классической механики. — 3-е изд. — М.: Наука, 1989. — 472 с.
[4] Бухгольц Н.Н. Основной курс теоретической механики. Часть 1. Кинематика, статика, динамика материальной точки. 6-е изд. - М., Наука, 1965. 468 с.

- Ingus's блог
- Войдите на сайт для отправки комментариев
- 9576 просмотров

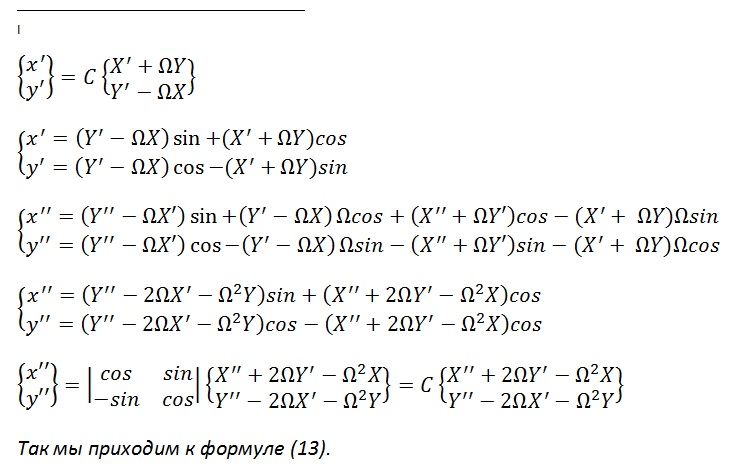
.JPG)
.JPG)

