Эфемериды Луны за 20 лет | Лаборатория космических исследований

Лаборатория космических исследований

Ульяновская секция Поволжского отделения Российской Академии Космонавтики им. К. Э. Циолковского

Ульяновский Государственный Университет

Эфемериды Луны за 20 лет

Опубликовано Ingus в чт, 18/10/2012 - 18:45

Мною обработаны эфемеридные данные Луны за 20 лет с 01/01/2000 г. Полная таблица прилагается.

N - номер дня,

DMY - дата,

Ra - прямое восхождение в часах,

D - склонение в градусах,

R - расстояние до центра Земли, км

Ph - фаза,

SIZ - сизигия (полнолуние/новолуние)

APS - апсида (перигей/апогей)

MD - лунный день, порядковый номер дня в синодическом месяце

N	DMY	Ra	D	R	Ph	SIZ	APS	MD
1	01.01.2000	14,45	-9,0	400926	27,2%			25
2	02.01.2000	15,22	-12,7	403707	19,1%			26
3	03.01.2000	16,01	-15,8	405479	12,3%			27
4	04.01.2000	16,81	-18,3	406323	6,8%			28
5	05.01.2000	17,64	-20,0	406346	2,8%		A	29
6	06.01.2000	18,48	-20,9	405660	0,6%			30
7	07.01.2000	19,33	-20,8	404359	0,1%	NM		1
8	08.01.2000	20,18	-19,8	402509	1,4%			2

Вложение	Размер
moon_ 2020.xls	1.59 Мб

Ingus's блог
Войдите на сайт для отправки комментариев
6949 просмотров

Опубликовано Иван в пн, 18/02/2013 - 16:41.

Ingus пишет:

Мною обработаны эфемеридные данные Луны за 20 лет

Как гарантируется достоверность данных и кто такой Ingus?

Войдите на сайт для отправки комментариев

Опубликовано zhvictorm в сб, 20/10/2012 - 03:48.

Уважаемый Ingus! Можно ли эфемериды перевести в кеплеровские параметры орбиты?

Войдите на сайт для отправки комментариев

Опубликовано Ingus в чт, 25/10/2012 - 17:25.

Да можно, наверное. Берем прямое восхождение, склонение, которые суть углы в сферической системе координат, расстояние до объекта и понеслась. Цитируя Википедию:

Вычисление кеплеровых элементов

Рассмотрим следующую задачу: пусть имеется невозмущённое движение и известны вектор положения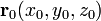 $\mathbf r_0(x_0,y_0,z_0)$ и вектор скорости $\mathbf \dot r(\dot x_0, \dot y_0, \dot z_0)$ на момент времени $t$ . Найдём кеплеровы элементы орбиты.

Прежде всего, вычислим большую полуось:

$r^2_0 = x^2_0 + y^2_0 + z^2_0$

$\dot r^2_0 = \dot x^2_0 + \dot y^2_0 + \dot z^2_0$

$r_0 \cdot \dot r_0 = x_0 \cdot \dot x_0 + y_0 \cdot \dot y_0 + z_0 \cdot \dot z_0$

По интегралу энергии:

(1) $\frac {1}{a} = \frac {2}{r_0} - \frac {v^2_0}{k}$ , где k — гравитационный параметр равный произведению гравитационной постоянной на массу небесного тела, для Земли K = 3,986005·10⁵км³/c², для Солнца K = 1,32712438·10¹¹ км³/c².

Следовательно, по формуле (1) находим $a$ .

______

(Есть правда загвоздка с определением расстояния не прямыми методами. Вот к примеру, расстояние до Луны у меня вычисляется через ее видимый угловой и реальный диаметр. А если бы я не знал реальный диаметр Луны? Если бы не померил его рулеткой?).

Собственно Луна - некеплеровская чуть больше, чем совсем. Возмущенная она до предела. Но траектория ее эфемеридная четко рисуется на сфере неизвестного радиуса и представляет собой незамкнутую кривую, напоминающую ромашку от сферического маятника с ненулевым моментом вращения относительно оси, проходящей вертикально через точку подвеса. Радиус сфер можно конечно и уточнить прямым лазерным ну или там радиолокационным измрением.

Попутно созрел вопрос: можно ли доказать, что орбита луны с всеми ее пертурбацими лежит на поверхности тора, и что из этого может следовать?

http://www.spacephys.ru/dvizhenie-luny-otnositelno-nebesnogo-ekvatora

Войдите на сайт для отправки комментариев

Ульяновская секция Поволжского отделения Российской Академии Космонавтики им. К. Э. Циолковского

Академия космонавтики

Лаборатория

Геопортал

Проекты

Кафедра Теор. Физики

Знание-Сила

Конференции

Сотрудники

Вход для пользователей

Наши партнеры

Вычисление кеплеровых элементов

Солнце в реальном времени

Снимки из Космоса

Спутниковые карты

МКС

NOAA-19

АИСТ-2

Последние обновления

Последние комментарии

Новые обсуждения форума