VI. Геометрия или - Где мы живем?

В предыдущем разделе мы озаботились тем, чтобы понять, что же обеспечивает передачу сил тяготения между телами. Для обозначения такого странного явления физики придумали понятие поля, т.е. чего-то невидимого, что "переносит" через пространство воздействие от одного тела к другому.

        Парадоксальным  здесь является то, что такое взаимодействие совершенно не зависит от наличия материи между телами. Как мы сейчас знаем, вакуум между планетами, а тем более между звездами, и уж тем более между галактиками, настолько разряжен, что его нельзя создать в земных условиях с помощью различного типа насосов. Значит - это нечто присуще самому пространству, т.е. той сущности которая введена нами для объяснения того, что между материальными телами есть какие-то расстояния.

     Буквально это означает, что есть тела, которые соприкасаются, а есть такие, которые не соприкасаются между собой. Более того, есть различного рода объекты - поля, леса, горы, моря, люди, животные, деревья, которых мы не видим с того места, где находимся, но если пройти сто метров, километр, сто километров и т.д., то мы увидим новые поля, горы, реки, моря и т.д. Причем для целого ряда объектов со временем не меняется такая сущность, которую мы называем расстоянием. Мы можем, скажем ехать из одного города в другой на машине с одной скоростью, на лошади с другой, на самолете с третьей, и каждый раз мы будем добираться за разное время. Однако, если умножить скорость на время, то получим, что расстояние всегда будет одним и тем же.

      Эта же сущность лежит в основе понимания того, что есть предметы разной длины. Размер клавиатуры у компьютера один, а у стола, на котором стоит компьютер, длина другая. Но опять же, если сравнить клавиатуру или стол утром и вечером, то можно придти к выводу, что их длины не изменились. Значит,  в нашем мире есть нечто постоянное, что очень важно, если мы хотим  что-то делать в разных местах и с разными, но похожими предметами. Это свойство протяженности объектов и расстояний до них. Конечно, часть предметов и объектов, например, живые организмы движутся и меняют свои размеры, но это связано с какими-то процессами внутри них. А глобальная структура видимого нами привычного мира обладает жестким "скелетом" протяженностей, который  не меняется со временем. Именно так себе представляли мир древние греки.

     Сейчас мы знаем, что это не совсем так, но отличия от этих представлений крайне не значительны, так что человек в обыденной жизни этого не заметит. Этот жесткий костяк мира и стали называть пространством. В работах древнегреческих математиков, в первую очередь Евклида, были установлены простые правила (аксиомы), которым подчиняются различные расстояния и длины в нашем мире. Всю совокупность таких расстояний и свойств, их связывающих, стали называть геометрией или совокупностью метрических отношений между телами. Позже появилось название евклидовой геометрии, когда понадобилось отличать различные костяки возможных миров и их частей с различными свойствами связи расстояний и длин в них. Основным свойством этих правил - аксиом Евклида, является то, что наш мир "прямой". Конечно, в нем есть и не прямые линии и поверхности, и есть такие, которые очень сложно устроены, например, раковины моллюсков.

    Для описания всех свойств таких линий и поверхностей, достаточно вычислить все "прямые" расстояния до точек этой линии или поверхности от некоторой одной заданной точки - начала отсчета, пользуясь правилами Евклида. Поэтому можно условно назвать наше пространство "прямым". Это, конечно, может понадобиться, если указать какие-то "кривые" миры или геометрии.  На протяжении более, чем 2000 лет ученые не представляли себе, что геометрия может быть какой-то другой, отличной от "прямой" или евклидовой. 

VII. Может ли мир быть кривым?

       Первые сомнения в том, что совокупность метрических отношений между объектами всегда подчиняется правилам Евклида, были высказаны нашим замечательным ученым-математиком Николаем Ивановичем Лобачевским. Трудно сказать, что именно послужило толчком к новому взгляду на понимание геометрии, но вполне вероятно, что этим толчком было обдумывание странного понятия "поле", которое появилось в XIX веке. Раз поле не видимо, но как-то распределено в пространстве, то нельзя ли предположить, что поле и есть свойство самого пространства. Но такой взгляд полностью противоречит представлениям евклидовой, или "прямой" геометрии.  Геометрия - это в представлениях ученых жесткий неизменный костяк метрических отношений между материальными телами. Он дан свыше таким, как он есть,  и обсуждать здесь нечего. 

     Однако Лобачевский выяснил, что понятие параллельности прямых на самом деле может быть без особых сложностей распространено на некоторые кривые линии, лежащие на кривых поверхностях. Как определяется параллельность прямых по правилам Евклида? Если прямые разнесены на некоторое расстояние, то единственный способ проверить их параллельность - это взять какой-нибудь кусочек или отрезок одной прямой, перенести его по определенным правилам к другой прямой, и сравнить пренесенный отрезок с таким же отрезком на удаленной прямой. Если отрезки в точности совпадут, то прямые параллельны. Однако в этой методике есть одно слабое место. А как следует устанавливать правила переноса отрезков для их сравнения? При переносе, если Вы не ориентируетесь по внешним предметам, вы можете запросто случайно изменить направление отрезка и Ваше сравнение будет не верным! Как быть? Самый простой способ - это "разлиновать" ту местность, через которую Вы проносите отрезок параллельными прямыми. Тогда при переносе Вы можете постоянно сравнивать направление своего отрезка с отрезками линий, нарисованных на местности. В этом случае Вы не ошибетесь! В результате процесс сравнения становится вроде бы понятным и ясным. Однако и здесь все не так просто.

     Можно себе представить такую ситуацию. Вы поручили кому-то разлиновать местность параллельными прямыми перед тем, как  Вы решили проверить параллельность некоторых прямых. Но Вам попался шутник. Он взял и линии слегка сделал не параллельными, так что Вы этого без специальной проверки не обнаруживаете. В результате, проведя эксперимент, Вы можете сделать неверный вывод. Но такую ситуацию можно исключить с помощью проверки в евклидовом пространстве и пожурить шутника. А что будет, если взять такую местность, на которой в принципе нельзя нарисовать  в обычном смысле прямые? Тогда понятие параллельных становится вообще не ясным. В качестве такой местности Лобачевский взял псевдосферу (см. рис.).

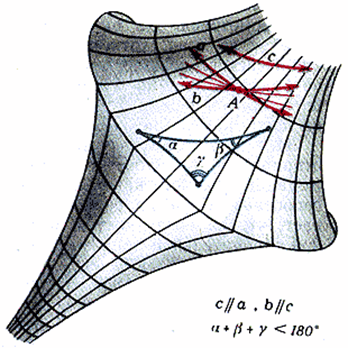
   Но можно было бы взять и обычную сферу.  Все линии, которые можно провести на псевдосфере (сфере), являются кривыми с точки зрения зрителя, смотрящего на эту сферу из вне. Поэтому, если мы разлинуем сферу (псевдосферу) с  помощью того же метода, что и в случае евклидова пространства, как это представлено на рисунке, то получим совокупность кривых, которые можно назвать параллельными. Пороверка параллельности по старому рецепту переноса не выявит никаких отличий от такой же процедуры в евклидовом пространстве. Но парадоксальным при этом оказывается факт, что эти параллельные пересекутся, что  явно противоречит пятому правилу-аксиоме Евклида.

       Лобачевский первым понял, что за этим стоит важнейший принцип, который должен быть перенесен с абстрактных поверхностей на окружающий нас мир.

      Фундаментальным вопросом теперь уже не математики, а именно физики, должен стать вопрос - а можно ли вообще провести в нашем мире строго прямые параллельные, которые могли бы служить основой проверки параллельности? Лобачевский об этом и заявил - такая проверка    может быть осуществлена только экспериментально. Был даже установлен простой способ такой проверки. Это вычисление суммы углов в треугольнике, стороны которого  строятся по принципу прямых в евклидовой геометрии. Для псевдосферы такая сумма должна быть меньше $180^o$ градусов, а для сферы - больше $180^o$.

      Таким образом, впервые было заявлено, что наш мир может быть "кривым"! Но это надо проверять, чем и должна заниматься физика. Но раз геометрия может быть кривой, то она может быть кривой по - разному! А раз так, то поле вполне может оказаться свойством  "кривизны" пространства. Однако для этого надо понять то, как могут отличаться друг от друга "кривые" пространства. 

VIII. Что такое кривизна?

      Надо отметить, что ученые - современники Лобачевского, далеко не сразу восприняли идеи Лобачевского. Однако был один замечательный ученый математик и физик XIX века -Иоганн Карл Фридрих Гаусс, который сразу понял важность открытия, сделанного Лобачевским.

    Он сразу сам решил проверить - является  ли наш мир прямым (сейчас часто говорят - плоским) или он является кривым. Для этого надо было измерить сумму углов треугольника, но какого? Если измерять сумму углов треугольника, нарисованного на бумаге или на другой ровной поверхности, то результат известен еще с древней Греции - сумма углов будет равна - $180^o$. Так какой же треугольник надо брать? Гаусс понял, что искать икривления надо на достаточно больших расстояниях, где нет заранее заданных поверхностей, а есть пустое пространство.  Пустого пространства, т.е. то что мы сейчас называем вакууммом вблизи поверхности Земли нет. Но можно предположить, что воздух не будет сильной помехой для измерения углов треугольника больших размеров. 

    Поэтому Гаусс расположил три небольших увеличительных (подзорные) трубы на вершинах трех гор в городе Гёттингене, где он тогда жил, работал и был директором Гёттингенской обсерватории. Расстояние между увеличительными трубами составляло примерно 40 км. С помощью этих увеличительных труб, которые сейчас принято называть в строительном деле - теодолитами, измерялась сумма углов треугольника, образованного прямыми, соединяющими увеличительные трубы. Оказалось, что сумма углов не отличается от $180^o$. Таким образом Гаусс первым проверил, что наш мир евклидов на расстояниях порядка десятков километров!

    Следует, правда, признать, что такие измерения могут содержать существенные ошибки, если воздух между горами был нагрет не равномерно. В этом случае лучи света движутся не по прямым, а по искривленным траекториям. Это связано с изменением показателя преломления воздуха. Примером могут служит миражи, которые часто можно наблюдать в жаркую погоду над разогретой асфальтовой дорогой, или миражи, о которых сообщают путешественники, проходившие через пустыни.

     Хотя результат измерений, проведенных Гауссом, дал отрицательный результат, тем не менее идея о том, что геометрии могут быть разными, а не только евклидовой, постепенно стала завоевывать умы ученых. Если Лобачевского не понимали, Гаусс упоминал о работах Лобачевского и о своих трудах в этом направлении очень осторожно, то во второй половине XIX века появилась целая плеяда молодых ученых, которые не только восприняли эту идею, но и развили  новую теорию.  Однако заслуги Гаусса  не заканчивались на проведении измерений суммы углов треугольника. Гаусс ввел понятие кривизны поверхности, которое помогает выяснять то, как различаются разные кривые геометрии.

      Как показал Гаусс,  существует важная количественная характеристика искривления поверхности - называемая сейчас гауссовой кривизной. Смысл ее показан на рисунке. В каждой точке поверхности можно провести две "главные" линии, пересекающиеся в этой точке. На рисунке точка, где производится вычисление гауссовой кривизны, находится на месте пересечения двух черных кривых. Вблизи этой точки кривые почти не отличаются от участков окружностей с радиусами $R_1$ и $R_2$, соответственно. Если Вы сумели вычислить радиусы этих окружностей, а это делается по уже известным сравнительно простым правилам, то гауссова кривизна $K$ равна по определению произведению обратных радиусов:

$K=\frac{1}{R_1R_2}$.

Другая величина $H$, равная сумме обратных величин радиусов,:

$H=\frac{1}{R_1}+\frac{1}{R_2}$

называется средней кривизной поверхности в данной точке. Средняя и гауссова кривизна поверхностей быстро попали в обиход физики. Так средняя кривизна входит в формулу Лапласа для избыточного давления пара над искривленной поверхностью жидкости. Эта формула имеет прямое отношение к мыльным пузырям. Гауссова же кривизна входит в формулу для дисперсионного соотношения волн на поверхности жидкости при учете поверхностного нятяжения.  Это соотношение объясняет тот факт, почему рябь на поверхности жидкости почти не движется, в то время как длинные волны бегут сравнительно быстро. Это можно легко заметить на поверхности любого открытого водоема - реки, озера, моря.

      Но не только этим важна гауссова кривизна. Как доказал Гаусс, если просуммировать (взять интеграл) значения гауссовой кривизны во всех точках замкнутой (не имеющей края) поверхности и разделить полученную величину на $4\pi$, то получается всегда целое число:

$$\frac{1}{4\pi}\int\limits_{S}KdS =\chi(S) \in \{0,\pm 1, \pm 2,\cdots\} $$

     Это целое число называется эйлеровой характеристикой замкнутой поверхности. Об этой величине речь пойдет позже. Она является первым важным элементом нового раздела математики - топологии, возникшей на рубеже XIX и XX веков. Удивительным здесь является то, что все замкнутые поверхности можно отнести к одному из классов, для каждого из которых число $\chi(S)$ будет иметь определенное значение.

     Например, для сферы $\chi(S)=2$. Позже мы разберем вопрос о том, почему это число носит имя великого математика XVIII века Леонарда Эйлера и какое свойство поверхностей оно определяет. В дальнейшем мы поймем, что оно в более общем виде определяет и величину электрического заряда частиц. Для нас сейчас важно, что в обиход математики и физики XIX века был привнесен способ отличать поверхности по их кривизне. Поскольку,  как установил Лобачевский и его поддержал Гаусс,  геометрии могут быть разными кривыми даже у нашего физического пространства, то появился способ отличать разные кривые пространства по величине кривизны.

IX. Как измерить кривизну нашего пространства?

     Хотя идея Гаусса замечательна, но она содержит один недостаток. И этот недостаток в самой сути определения кривизны Гаусса, поскольку она является параметром внешней геометрии. Дело в том, что для вычисления ее экспериментальной величны необходимо уметь смотреть на наше пространство извне, т.е. из пространства большего числа измерений, наподобие того, как мы смотрим на поверхности в нашем пространстве. Как же быть? Ведь мы находимся в своем трехмерном пространстве и не можем увидеть себя со стороны! Мы можем лищь вычислять совокупность всевозможных расстояний от одних тел до других. Возникает вопрос - можно ли установить то, что наше пространство кривое только по этим данным, которые в совокупности и называются внутренней геометрией пространства.

     Полный ответ на это вопрос был найден в конце XIX века и  наиболее важный вклад в создание такой теории сделал выдающийся немецкий математик Георг Фридрих Бернхард Риман. Его именем называют теперь совокупность геометрий, которые могут быть описаны с помощью внутренних расстояний в пространстве при условии, что в малой окрестности каждой точки такого пространства оно почти не отличается от плоского (прямого или евклидова). Это так называемые римановы геомерии. Риман ввел понятие внутренней кривизны пространства, что дало возможность впоследствии использовать такой подход в приложении к физическим задачам, не пытаясь угадать - находится ли наше физическое пространство внутри другого пространства большего числа измерений.

     Введение кривизны Римана стало важным шагом на пути создания Общей теории относительности (ОТО), но лишило теорию простого и наглядного представления о том, что же происходит в кривом мире, если его свойства меняются со временем. Формула для кривизны Римана выглядит намного сложнее, чем формула для кривизны Гаусса. Поэтому мы здесь ее не приводим.

    В XIX веке понимали, что метод Римана приводит к очень сложным уравнениям, если мы хотим избавиться  от необоснованных, с точки зрения эксперимента, размышлений о дополнительных измерениях. Поэтому многие ученые придерживались точки зрения, что кривизну пространства полезнее рассматривать именно с точки зрения внешней геометрии. Наиболее точное выражение такой точки зрения высказал еще один выдающийся математик XIX века - Уильям Клиффорд. Его точка зрения была изложена на одном из конгрессов математиков в конце XIX века следующими словами:

"Я считаю:

1. Что малые участки пространства действительно аналогичны небольшим холмам  на поверхности, которая в среднем является плоской, а именно: там несправедливы обычные законы геометрии.

2. Что это свойство искривленности или деформации непрерывно переходит с одного участка пространства на другой наподобие волны.

3. Что такое изменение кривизны  пространства  и есть  то, что реально происходит в явлении, которое  мы называем движением материи, будь она весомая или эфирная .

4. Что в физическом мире не происходит ничего, кроме таких изменений, подчиняющихся (возможно) закону непрерывности ."

(Цитируется по книге: Альберт Эйнштейн и теория Гравитации. М.: Изд. Мир, 1979 г.)

      Эти слова стали для многих ученых путеводной звездой в построении теории материи как проявления свойств самого пространства. В том числе, так себе представлял взаимоотношения пространства и материи Альберт Эйнштейн. Однако он не сумел воплотить в жизнь подход, который озвучил Клиффорд. И причиной этому является то, что ни тогда ни даже сейчас у нас нет пока прямых доказательств, что физическое пространство является лишь малой частью невообразимо огромного другого пространства, которое фантасты часто называют гипер-пространством, некоторые физики (Блохинцев) - Метапространством (видимо, по аналогии с понятием Метагалактики), а математики назвают объемлющим пространстом или пространством, в которое вложено наше физическое пространство (наподобие поверхности), имеющее размерность 3.