Отчет второго этапа
1. Метод многомасштабных разложений для анализа космологической динамики
(по статье Журавлев В.М., Червон С.В. )
Одним из эффективных методов асимптотического анализа моделей космологической динамики, являются методы качественного анализа динамических систем. Эти методы широко используются в различных областях математического моделирования систем [1,2,3,4,5,6]. Такие методы дают полезную информацию общего характера и позволяют понять, при каких условиях система асимптотически стремится к тому или иному состоянию. Вместе с тем, в случае, если необходимо получить достаточно точную информацию о характере решений при тех или иных начальных условиях, такие методы оказываются недостаточно эффективными. Для решения задач анализа текущего состояния систем значительно более полезными оказываются методы приближенного анализа, построенные на разложении решений в ряды по малому параметру. Среди таких методов, который редко используется в задачах космологии является метод многомасштабных разложений (ММР).
Исходной областью применения ММР, по всей видимости, следует считать механику и теорию волновых процессов [7,8]. Основная идея ММР сводится к представлению зависимости исходного процесса от времени и координат в форме зависимости от более широкого круга переменных, которые связаны с исходными переменными масштабными множителями, содержащими малые параметры модели в различных степенях. Отличие метода многомасштабных разложений от простого метода малого параметра состоит в том, что введение новых ``медленных'' или ``быстрых'' переменных позволяет улучшать сходимость рядов по этому малому параметру. Для управления скоростью сходимости рядов ММР содержит специфическое средство, которое часто называется процедурой устранения резонансов. Смысл этой процедуры состоит в том, что введение дополнительных независимых переменных (``медленных'' или ``быстрых'') порождает определенный произвол в выборе баланса между отдельными слагаемыми уравнений, полученных в результате разложений в ряд. Этот произвол позволяет подбирать зависимость элементов разложения в ряд таким образом, чтобы из ряда исключались слагаемые, имеющие степенной вид по независимым переменным (секулярные слагаемые), которые существенным образом ухудшают скорость сходимости рядов и уменьшают радиусы их сходимости.
В настоящей работе ММР применяется к задачам анализа динамических систем космологической эволюции для Вселенной со скалярным полем с самодействием в пространстве-времени Фридмана-Робертсона-Уокера. Хотя эта модель изучена достаточно полно, на ее примере можно показать особенности применения ММР к задачам космологической динамики, что в последствии может с пользой применено к более сложным моделям.
1.1 Исходная модель
В качестве примера использования многомасштабного разложения для описания космологической динамики рассмотрим простую модель со скалярным полем в плоском пространстве-времени Фридмана-Робертсона-Уокера. Основные уравнения этой модели имеют следующий вид: $$3H^2=\frac{1}{2} \dot{\phi}^2+V(\phi),$$ $$2\dot{H}=- \dot{\phi}^2,\tag{1.1}\label{EqSMP}$$ $$ \ddot{\phi}+3H\dot{\phi}+\frac{\partial V}{\partial \phi}=0.$$ Первые два уравнения этой системы представляют собой уравнения Эйнштейна, а последнее - уравнение поля. Последнее уравнение является следствием двух первых. Здесь $H=\dot{a}/a$ - параметр Хаббла, $a$ - масштабный фактор, $\phi$ - поле с потенциалом самодействия $V(\phi)$, $\tau$ - время в системе отсчета наблюдателя.
Введем безразмерные переменные, полагая: $\xi =H/H_0,~\eta = \phi/\Phi_0 ,~\tau = t /T_0$. В этих соотношениях $H_0,~\Phi_0$ и $T_0$ - некоторые постоянные соответствующих размерностей, которые должны определяться выбором требуемой асимптотики решений исходной системы. В результате подстановки в исходную систему безразмерных переменных приходим к системе уравнений в следующей форме: $$3H_0^2 \xi^2 =\frac{1}{2} \Phi_0^2\dot{\eta}^2+{\cal V}(\eta,\Phi_0),\tag{1.2}\label{EqBR}$$ $$2H_0T_0\dot{\xi}=- \Phi_0^2\dot{\eta}^2$$ В другой форме:
$$\frac{\alpha}{\beta}\dot{\xi}+3\xi^2 = \frac{1}{H_0^2}{\cal V}(\eta,\Phi_0),$$ $$\dot{\xi}=- \frac{1}{2}\beta\dot{\eta}^2.\tag{1.3}\label{EqBR1}$$ Здесь $V(\phi)={\cal V}(\eta,\Phi_0)$ и: $$\alpha=\frac{\Phi_0^2}{T_0^2H_0^2 },~~\beta=\frac{\Phi_0^2}{H_0T_0}.$$ Безразмерные параметры $\alpha$ и $\beta$ при заданной форме потенциала $V(\phi)$ и начальных условиях определяют динамику космологического процесса. Поскольку по определению параметр $\Gamma=H_0T_0$ - также безразмерен, то и $\Phi_0$ - также безразмерна.
1.2 Разложение по масштабу поля $\Phi_0$
Рассмотрим первый вариант выбора малого параметра, полагая $\Gamma=H_0T_0=1$ и $\Phi_0=\sqrt{\varepsilon}$ - малый параметр. Малое значение $\Phi_0$ означает малые отклонения поля от некоторого его фиксированного значения $\phi = \phi_{*}$, которое с помощью преобразования: $\phi'=\phi-\phi_{*}$ преобразуется к точке $\phi'=0$. При этом положение точки $\phi'=0$ может находиться и в минимуме и максимуме, как это показано на рис. 1,2, а также в любой другой точке оси $\phi$ (рис. 3). Иллюстрацией этого факта служат рисунки с положением точек $\phi=0$ для потенциала Хиггса: $$V = 1+\phi^4-\phi^2.\tag{1.4}\label{DefVH}$$

Рис. 1. Положение точки $\phi_{*}$ в локальном максимуме потенциала
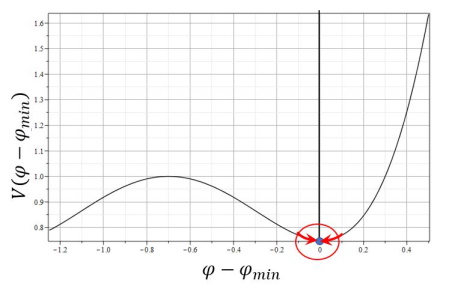
Рис. 2. Положение точки $\phi_{*}$ в локальном минимуме потенциала
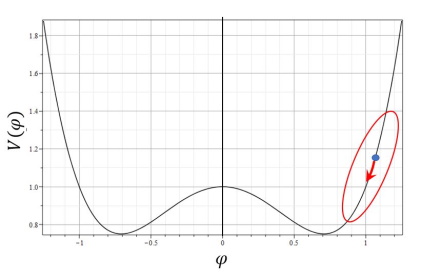
Рис. 3. Положение точки $\phi_{*}$ в произвольной точке оси $\phi$
Для выбора в качестве малого параметра масштаба поля $\phi$ следует полагать $\alpha=\beta$. Используя новые переменные, можно формально записать: $$\frac{1}{H_0^2}V(\phi)={\cal V}(\eta,\sqrt{\varepsilon}).$$ Предполагаемая малость параметра $\varepsilon$ позволяет в соответствии с общей идеологией многомасштабных разложений искать решения системы (\ref{EqBR1}) в форме зависимости от обычной $\tau$ и медленных переменных, которые будут иметь такой вид: $$\tau_1=\sqrt{\varepsilon} \tau,~\tau_2=\varepsilon \tau,~\ldots.$$ Отсюда имеем для любой функции $F(\tau)={\cal F}(\tau,\tau_1,\tau_2,\ldots)$: $$\frac{d}{d\tau}F(t) = \left(\frac{\partial}{\partial \tau}+\sqrt{\varepsilon}\frac{\partial}{\partial \tau_1}+\varepsilon\frac{\partial}{\partial\tau_2}+\cdots\right){\cal F}(\tau,\tau_1,\tau_2,\ldots)$$
Представим потенциал $V(\phi)$ в виде ряда разложения по $\phi$: $$V(\phi)=V_0+ V_1\phi+V_2\phi^2+\cdots.$$ Отсюда: $${\cal V}(\eta,\sqrt{\varepsilon})=v_0+v_1\eta\sqrt{\varepsilon}+v_2\eta^2\varepsilon+\cdots,$$ где $v_i = H_0^{-2}V_i,~i=0,1,\ldots$ - безразмерные параметры потенциала.
Аналогично, решение для $\xi(t)$ и $\eta(t)$ будем искать в следующем виде:
$$\xi=\xi_0(\tau,\tau_1,\tau_2,\ldots)+\sqrt{\varepsilon}\xi_1(\tau,\tau_1,\tau_2,\ldots)+
\varepsilon \xi_2(\tau,\tau_1,\tau_2,\ldots)+\cdots,$$ $$\eta=\eta_0(\tau,\tau_1,\tau_2,\ldots)+\sqrt{\varepsilon}\eta_1(\tau,\tau_1,\tau_2,\ldots)+\varepsilon \eta_2(\tau,\tau_1,\tau_2,\ldots)+\cdots.$$
Подставляя эти соотношения в первое уравнение системы (\ref{EqBR1}),
относительно первых трех элементов разложения имеем: $$\left(\frac{\partial}{\partial \tau}+\sqrt{\varepsilon}\frac{\partial}{\partial \tau_1}+\varepsilon\frac{\partial}{\partial \tau_2}+\cdots\right)\Big(\xi_0(\tau,\tau_1,\ldots)+\sqrt{\varepsilon}\xi_1(\tau,\tau_1,\ldots)+\varepsilon \xi_2(\tau,\tau_1,\ldots)+\cdots\Big)+$$ $$+3\Big(\xi_0(\tau,\tau_1,\ldots)+\sqrt{\varepsilon}\xi_1(\tau,\tau_1,\ldots)+\varepsilon \xi_2(\tau,\tau_1,\ldots)+\cdots\Big)^2=\tag{1.5}\label{Eqxi1}$$ $$=v_0+v_1\Big(\eta_0(\tau,\tau_1,\ldots)+\sqrt{\varepsilon}\eta_1(\tau,\tau_1,\ldots)\Big)\sqrt{\varepsilon}+v_2(\eta_0^2\varepsilon+2\eta_0\eta_1\varepsilon^{3/2}) + v_3\eta_0^3\varepsilon^{3/2}+\cdots.$$
Первые четыре уравнения системы уравнений разложения по порядкам $\varepsilon^{1/2}$ имеют такой вид: $$\varepsilon^{0}:\frac{\partial\xi_0}{ \partial \tau}+3\xi_0^2=v_0,$$ $$\varepsilon^{1/2}:\frac{\partial\xi_1}{ \partial \tau}+\frac{\partial\xi_0}{ \partial \tau_1}+6\xi_0\xi_1=v_1\eta_0,$$ $$\varepsilon^{1}:\frac{\partial\xi_2}{ \partial\tau}+\frac{\partial\xi_1}{\partial\tau_1}+\frac{\partial\xi_0}{\partial\tau_2}+6\xi_0\xi_2+3\xi_1^2=v_1\eta_1+v_2\eta_0^2,\tag{1.6}\label{EqPi}$$ $$\varepsilon^{3/2}:\frac{\partial\xi_3}{\partial\tau}+\frac{\partial\xi_2}{\partial\tau_1}+\frac{\partial\xi_1}{\partial\tau_2}+\frac{\partial\xi_0}{\partial \tau_3} +6(\xi_0\xi_3+\xi_1\xi_2)=v_1\eta_2+2v_2\eta_0\eta_1+v_3\eta_0^3,$$ $$\cdots$$ Аналогично, находим разложение второго уравнения системы (\ref{EqBR1}). После подстановки рядов, находим: $$\left(\frac{\partial}{ \partial \tau}+\sqrt{\varepsilon}\frac{\partial}{\partial \tau_1}+\varepsilon\frac{\partial}{\partial \tau_2}+\cdots\right)\Big(\xi_0(\tau,\tau_1,\ldots)+\sqrt{\varepsilon}\xi_1(\tau,\tau_1,\ldots)+\varepsilon \xi_2(\tau,\tau_1,\ldots)\Big)=\tag{1.6}\label{Eqeta1}$$ $$=-\frac{1}{2}\varepsilon\left(\frac{\partial\eta_0}{\partial \tau}+\sqrt{\varepsilon}\frac{\partial\eta_0}{\partial \tau_1}+\varepsilon \frac{\partial\eta_0}{\partial \tau_2}\right.+\left.\sqrt{\varepsilon}\frac{\partial\eta_1}{\partial \tau}+\varepsilon\frac{\partial\eta_0}{\partial \tau_1}+\varepsilon\frac{\partial\eta_2}{\partial \tau_2}+\ldots\right)^2.$$ Первые три уравнения системы уравнений разложения последнего уравнения по порядкам $\varepsilon^{1/2}$ имеют такой вид:
$$\varepsilon^{0}:\frac{\partial\xi_0}{ \partial \tau}=0,$$ $$\varepsilon^{1/2}:\frac{\partial\xi_1}{\partial \tau}+\frac{\partial\xi_0}{\partial \tau_1}=0,\tag{1.7}\label{EqPhi}$$ $$\varepsilon^{1}:\frac{\partial\xi_2}{\partial \tau}+\frac{\partial\xi_1}{\partial \tau_1}+\frac{\partial\xi_0}{\partial \tau_2}=-\frac{1}{2}\left(\frac{\partial\eta_0}{ \partial \tau}\right)^2,$$ $$\varepsilon^{3/2}:\frac{\partial\xi_3}{ \partial \tau}+\frac{\partial\xi_2}{\partial \tau_1}+\frac{\partial\xi_1}{\partial \tau_2}+\frac{\partial\xi_0}{ \partial \tau_3}=-\frac{1}{2}\frac{\partial\eta_0}{ \partial \tau}\left(\frac{\partial\eta_0}{ \partial \tau_1}+\frac{\partial\eta_1}{ \partial \tau}\right),$$ $$\ldots$$
1.3. Решение системы уравнений
Решение первых двух уравнений систем (\ref{EqPi}) и (\ref{Eqeta1}) приводит к следующему решению относительно $\xi_0$: $$\xi_0 = \pm \sqrt{\frac{v_0}{3}}=\pm \Lambda.\tag{1.8}\label{Solxi0}$$ Здесь и далее введено обозначение: $\Lambda=\sqrt{v_0/3}$. Для того, чтобы это решение имело смысл, необходимо выполнение $v_0\ge 0$, что, как известно, является следствием условия энергодоминантности. Поскольку $v_0=const$, имеем: $\xi_0=const$.
В результате, решение в первом порядке имеет такой вид: $$\xi_1=\pm\frac{v_1}{6\Lambda}\eta_0(\tau_1,\tau_2,\ldots).$$ При этом функции $\xi_1$ и $\eta_0$ зависят только от медленных переменных: $\xi_1=\xi_1(\tau_1,\tau_2,\ldots), \eta_0=\eta_0(\tau_1,\tau_2,\ldots)$.
Решение во втором порядке теперь можно записать так: $$\xi_2 = \pm\frac{1}{8\sqrt{3v_0}}\Big(4v_0v_1\eta_1(\tau,\tau_1,\ldots)+(4v_0v_2-v_1^2)\eta_0^2(\tau_1,\tau_2,\ldots)\Big).\tag{1.9}\label{Solxi2}$$ При этом из уравнения в порядке $\varepsilon^{3/2}$ системы (\ref{EqPhi}) для функции $\eta_1(\tau,\tau_1,\ldots)$ получаем уравнение: $$\frac{\partial\eta_1}{\partial\tau}+\frac{\partial\eta_0}{\partial\tau_1}=0.$$ Отсюда: $$\eta_1 = - \tau \frac{\partial \eta_0}{\partial\tau_1}+C_1(\tau_1,\tau_2,\dots),$$ где $C_1(\tau_1,\tau_2,\ldots)$ - постоянная интегрирования по $\tau$. Заметим, что зависимость $\eta_0=\eta_0(\tau_1,\tau_2,\ldots)$ от $\tau_1$ остается пока не определенной. Этим можно воспользоваться для того, чтобы исключить в решении для $\eta_1$ слагаемого растущего линейно вместе с $\tau$. Такие слагаемые часто называют резонансными или секулярными. Наличие таких слагаемых приводит к быстрой расходимости ряда по $\varepsilon$ с ростом
$\tau$. Полагая $\eta_0=\eta_0(\tau_2,\ldots)$, мы исключаем зависимость $\eta_1$ от $\tau$.
Такая процедура и называется процедурой устранения резонансов. В данном случае и $\xi_2$ также не будет зависеть от $\tau$, но будет зависеть и от медленных переменных.
Третий порядок уравнения для масштабного фактора теперь можно записать в следующей форме:
$$\xi_3=\frac{1}{6}\sqrt{\frac{3}{v_0}}\left(v_1\eta_2+2v_2\eta_0\eta_1+v_3\eta_0^3-6\xi_1\xi_2)\right).$$ При этом выполняются еще и следующие соотношения: $$\xi_2(\tau_1,\tau_2,\ldots)=-\tau_1\frac{\partial\xi_1}{\partial\tau_2}+\xi^{(0)}_1(\tau_2,\ldots),$$ которые определяют зависимость $\xi_2$ от медленной переменной $\tau_1$. С формальной точки зрения линейная зависимость $\xi_2(\tau_1,\tau_2,\ldots)$ от $\tau_1$ также может рассматриваться как ``резонансное'' слагаемое, приводящее к ускоренной расходимости ряда. Поэтому его также можно устранить, полагая $\xi_1=\xi_1(\tau_2,\ldots)$. В следующих порядках можно продолжать применять аналогичную процедуру и далее.
1.4 Решение для масштабного фактора
Поскольку $\xi_0,~\xi_1$ и $\xi_2$ - не зависят от быстрой переменной, то можно выяснить характер космологического расширения. Из определения $\xi$ с точностью до $\varepsilon$ имеем: $$H = H_0\Big(\xi_0+\sqrt{\varepsilon}\xi_1+\varepsilon\xi_2+\varepsilon^{3/2}\xi_3+\ldots\Big) = H_0\frac{\dot{a}}{a}=\frac{H_0}{a_0+\sqrt{\varepsilon}a_1+\varepsilon a_2+\varepsilon^{3/2}a_3+\ldots}\left(\frac{\partial a_0}{\partial \tau}+\right.$$ $$+\left.\sqrt{\varepsilon}\left(\frac{\partial a_0}{\partial \tau_1}+\frac{\partial a_1}{\partial \tau}\right)+\varepsilon \left(\frac{\partial a_0}{\partial \tau_1}+\frac{\partial a_1}{\partial \tau_1}+\frac{\partial a_2}{\partial \tau}+\ldots\right)+\ldots\right).$$
Отсюда приходим к следующей системе уравнений для вычисления эволюции масштабного фактора $a=a_0+\sqrt{\varepsilon}a_1+\varepsilon a_2+\ldots$. Имеем: $$\xi_0 = \frac{\partial \ln a_0}{\partial \tau},$$ $$\xi_1 = \frac{1}{a_0}\left(\frac{\partial a_0}{\partial \tau_1}-\frac{a_1}{a_0}\frac{\partial a_0}{\partial \tau}+\frac{\partial a_1}{\partial \tau}\right),$$ $$\xi_2 = -\frac{\partial a_0}{\partial \tau}\left(\frac{a_2}{a_0^2}-\frac{a_1^2}{a_0^3}\right)-\left(\frac{\partial a_0}{\partial \tau_1}+\frac{\partial a_1}{\partial \tau}\right)\frac{a_1}{a_0^2}+\left(\frac{\partial a_0}{\partial \tau_2}+\frac{\partial a_1}{\partial \tau_1}+\frac{\partial a_2}{\partial \tau}\right)\frac{1}{a_0}. $$ Отсюда находим: $$a_0 = A_0(\tau_1,\tau_2,\ldots) e^{\tau \sqrt{v_0/3} }.$$
В первом порядке уравнение для $a_1$ приводится к виду: $$\frac{\partial a_1}{\partial \tau}-\sqrt{\Lambda}a_1=A_0e^{\Lambda \tau}\left(\frac{v_1}{6\Lambda}\eta_0-\frac{\partial \ln A_0}{\partial \tau_1}\right).$$ Условием отсутствия резонанса в этом уравнении, является обращение в ноль правой части этого уравнения, что приводит к уравнению: $$A_0\frac{v_1}{6\Lambda}\eta_0 -\frac{\partial A_0}{\partial \tau_1}=0.$$ Отсюда при условии $\xi_1=const$ следует: $$A_0 = A_{00}\exp{\Big( \frac{v_1}{6\Lambda}\eta_0\tau_1\Big)}.\tag{1.10}\label{SolA0}$$ Постоянная интегрирования $A_{00}$ может зависеть от $\tau_2,\ldots$. Заметим, что знак экспоненты в (\ref{SolA0}) определяется как знаком $v_1$, т.е. знаком коэффициента ряда Тейлора разложения потенциала в нуле, так и знаком самого поля в нулевом порядке. Следовательно, при противоположных знаках $\eta_0$ и $v_1$ скорость инфляции будет уменьшаться по сравнению с нулевым порядком.
Полученные в первых двух порядках решения для масштабного фактора можно представить в следующем виде: $$a = e^{\Lambda \tau}\left(A_{00}\exp{\Big( \frac{v_1}{6\Lambda}\eta_0\tau \sqrt{\varepsilon}\Big)}+\sqrt{\varepsilon}A_{10}\right)+O(\varepsilon).\tag{1.11}\label{Sola1}$$
1.5 Разложение по параметру медленного скатывания
Рассмотрим теперь результаты анализа уравнений в случае выбора масштабов в соответствии с соотношениями: $\Phi_0=1, H_0T_0=\varepsilon^{-1}$ , где $\varepsilon<<1$ - новый малый параметр. В обезразмеренном виде параметр медленного скатывания: $$p = -\frac{\dot{H}}{H^2},$$ будет иметь следующий вид: $$p = -\frac{1}{H_0T_0}\frac{\dot{\xi}}{\xi^2}=-\varepsilon \frac{\dot{\xi}}{\xi^2},$$ т.е. является величиной первого порядка малости по $\varepsilon$. Это означает, что $\varepsilon=(H_0T_0)^{-1}$ можно интерпретировать как масштаб медленного скатывания.
Переходя к обезразмеренным уравнениям (\ref{EqBR1}), находим в данном случае: $$\alpha = \varepsilon^2,~~\beta=\varepsilon.$$ Уравнения (\ref{EqBR1}) при таком выборе параметров примут следующий вид: $$\varepsilon\dot{\xi}+3\xi^2 = \frac{1}{H_0^2}{\cal V}(\eta),\tag{1.12}\label{EqBRm20}$$ $$\dot{\xi}=- \frac{1}{2}\varepsilon\dot{\eta}^2.$$ Данная система является сингулярной, поскольку в двух уравнениях малый параметр стоит при старшей производной. Для устранения этого недостатка введем новую переменную времени, полагая $\theta = \tau \varepsilon^{-1} = H_0 t$. Для новой переменной уравнения примут такой вид: $$\dot{\xi}+3\xi^2 = \frac{1}{H_0^2}{\cal V}(\eta),\tag{1.13}\label{EqBR2}$$ $$\dot{\xi}=- \frac{1}{2}\dot{\eta}^2.$$
Неясным элементом последней системы уравнений является слагаемое в правой части первого уравнения, связанное с потенциалом. Суть проблемы состоит в том, как соотносятся значения функции ${\cal V}(\eta)$ по отношению к $H_0^2$. Имеются две возможности. Первая состоит в том, что значения величины $H_0^{-2}{\cal V}(\eta)$ имеют порядок $1$, а другая состоит в том, что порядок единицы имеет величина $T_0^2{\cal V}(\eta)$. В первом случае уравнения не содержат малого параметра $\varepsilon$, а во втором слагаемое с потенциалом будет иметь порядок $\varepsilon^2$. В общем случае можно предполагать, что функциональная зависимость потенциала от $\eta$ может быть разбита на две части. Первая имеет порядок единицы в случае $H_0^2{\cal V}$, а вторая - в случае $T_0^2{\cal V}$. В соответствии с этим будем полагать:
$$H_0^{-2}{\cal V} = V_0(\eta) + \varepsilon^2 U(\eta),$$ где ${\cal V}_0(\eta)$ и $U(\eta)$ функции имеющие порядок $1$.
1.6 Уравнения в првых порядках теории возмущений
Рассмотрим случай, соответствующий ситуации $V_0 = v_0=const$. В этом случае $v_0$ можно рассматривать как космологическую постоянную. Будем строить разложение по $\varepsilon$, полагая: $$\xi=\xi_0+\varepsilon\xi_1+\ldots, \eta = \eta_0+\varepsilon\eta_0+\ldots.$$ Зависимость коэффициентов разложения от медленных переменных будет определяться переменными $\theta_i = \varepsilon^i \theta, i=0,1,2,\ldots$. Ограничимся для данного разложения только первыми двумя порядками. В результате имеем следующую систему уравнений по порядкам первого уравнения $$\dot{\xi}_0 + 3\xi_0^2 = v_0,$$ $$\dot{\xi}_1 + \frac{\partial \xi_0}{\partial \theta_1} + 6\xi_0\xi_1 = 0,\tag{1.14}\label{EqB2xi}$$ $$\dot{\xi}_2 + \frac{\partial \xi_1}{\partial \theta_1} + \frac{\partial \xi_0}{\partial \theta_2} + 6\xi_0\xi_2 + 3\xi_1^2 = U(\eta_0).$$ Аналогично, для второго уравнения системы (\ref{EqBR2}) имеем: $$\dot{\xi}_0 = -\frac{1}{2}\dot{\eta_0}^2,$$ $$\dot{\xi}_1 +\frac{\partial \xi_0}{\partial \theta_1} =
-\dot{\eta_0}\left(\dot{\eta_1}+\frac{\partial \eta_0}{\partial \theta_1}\right),\tag{1.15}\label{EqB2eta}$$ $$\dot{\xi}_2 + \frac{\partial \xi_1}{\partial \theta_1} + \frac{\partial \xi_0}{\partial \theta_2} = -\dot{\eta_0}\left(\dot{\eta_2}+\frac{\partial \eta_1}{\partial \theta_1} + \frac{\partial \eta_0}{\partial \theta_2}\right)-\frac{1}{2}\left(\dot{\eta_1}\frac{\partial\eta_0}{\partial \theta_1}\right)^2.$$
1.6.1 Нулевой порядок
Решение в нулевом порядке для $\xi_0$ строится с помощью формальной замены: $$\xi_0 = \frac{1}{3}\frac{d \ln u}{d t}.\tag{1.16}\label{Subxi0}$$ Для $\theta$ имеем уравнение:
$$\ddot{u} = 3v_0 u.$$ Общее решение для $u$ имеет следующий вид: $$u = C_1 e^{\mu \theta} + C_2 e^{-\mu \theta}.$$ Здесь $\mu^2=3v_0$. Решение для $\xi_0$ имеет следующий вид:
$$\xi_0 = \frac{\mu}{3}\frac{1 - C e^{-2\mu \theta}}{1 + C e^{-2\mu \theta}}.$$ Здесь $C=C_2/C_1$. Поскольку $\dot{\xi_0}<0$, то имеются ограничения на выбор $C$. Для того, чтобы функция $\xi_0$ была монотонно убывающей, необходимо, чтобы $C < 0$. Значение $C$ определяет в этом случае положение космологической сингулярности. Если полагать, что момент времени космологической сингулярности выбирается равным $t=0$, то $C=1$. В результате решение для $\xi_0$ можно записать в следующем виде: $$\xi_0 = \frac{\mu}{3}\tanh^{-1}(\mu \theta).\tag{1.17}\label{Solxi00}$$ Отсюда: $$\dot{\xi_0} = -\frac{\mu^2}{3 \sinh^2(\mu \theta)}<0,$$ $$a_0 = A_0\sinh^{1/3}(\mu \theta).\tag{1.18}\label{SolP0}$$ Здесь $a_0(\theta)$ - масштабный фактор в нулевом порядке, $A_0$ - постоянная интегрирования.
Используя (\ref{SolP0}), уравнение для поля в нулевом порядке привести к такому виду:
$$\dot{\eta_0} = s \frac{\sqrt{2}\mu}{\sqrt{3}\sinh(\mu \theta)},~~s=\pm 1.$$ Отсюда находим:
$$\eta_0 = f_0+\int\frac{\mu d\theta}{\sinh(\mu \theta)} =f_0+\frac{s\sqrt{2}}{\sqrt{3}}\int\frac{d z}{z^2-1}=f_0+\frac{s}{\sqrt{6}}\ln\left(\frac{\cosh(\mu \theta)-1}{\cosh(\mu \theta)+1}\right)\tag{1.19}\label{Soleta0}$$
1.6.2 Первый порядок
В нулевом порядке решение для $\xi_0$ не содержит произвольных постоянных, которые могли бы зависеть от медленных переменных. Поэтому из (\ref{EqB2xi}) в первом порядке для $\xi_1$ имеем следующее уравнение: $$\dot{\xi}_1 = - 2\mu \tanh^{-1}(\mu t)\xi_1.$$ Отсюда находим:
$$\xi_1 = \frac{q_1(\tau_1,\ldots)}{\sinh^{2}(\mu \theta)},\tag{1.20}\label{Solxi1}$$ где $q_1=q_1(\tau_1,\ldots)$ - постоянная интегрирования, зависящая от медленных переменных.
В отличие от $\xi_0$ решение для $\eta_0$ содержит постоянную интегрирования, которая может зависеть от медленных переменных. В результате для $\eta_1$ имеем следующее уравнение:
$$\dot{\eta}_1 = -\frac{1}{\dot{\eta}_0}\left(\dot{\xi}_1+\dot{\eta}_0\frac{\partial f_0}{\partial \theta_1}\right)=\frac{2sq_1}{\sqrt{3}}\frac{\cosh(\mu \theta)}{\sinh^2(\mu \theta)}-\frac{\partial f_0}{\partial \theta_1}.\tag{1.21}\label{Eqeta11}$$ Отсюда: $$\eta_1 = -\frac{2sq_1}{\sqrt{3}\mu}\frac{1}{\sinh(\mu \theta)}-\frac{\partial f_0}{\partial \tau_1}\theta+f_1(\theta_1,\ldots).$$
Второе слагаемое в правой части последнего соотношения линейно по $\theta$ и является ``резонансным''. Для исключения его требуется полагать $$\frac{\partial f_0}{\partial \theta_1}=0,~~f_0=f_0(\theta_2,\ldots).$$ Таким образом, решение для $\eta_1$ будет следующим:
$$\eta_1 = -\frac{2sq_1}{\sqrt{3}\mu}\frac{1}{\sinh(\mu \theta)}+f_1(\theta_1,\ldots).\tag{1.22}\label{Soleta1}$$
1.6.3 Второй порядок
Уравнение для масштабного фактора во втором порядке с учетом первых двух можно записать в таком виде: $$\dot{\xi}_2 + \frac{\partial q_1}{\partial \theta_1}\frac{1}{\sinh^{2}(\mu \theta)} + 2\mu \tanh^{-1}(\mu t)\xi_2 + 3\frac{q_1^2}{\sinh^{4}(\mu \theta)} = U(\eta_0).\tag{1.23}\label{Eqxi2}$$ Решение этого уравнения зависит от вида функции $U(\eta_0)$. Поэтому для получения его явного вида необходимо выбрать определенный тип этой зависимости. Однако для выяснения наличия резонансных слагаемых в этом уравнении достаточно рассмотреть лишь некоторые компоненты ряда Тейлора функции $U(\eta_0)$ в нуле. Собственная функция уравнения (\ref{Eqxi2}) с точностью до постоянного множителя совпадает с $\sinh^{-2}(\mu\theta)$. Следовательно, интерес для исключения резонансов представляет лишь квадратичный по $\eta_0$ компонент ряда Тейлора, поскольку $\eta_0\sim \sinh^{-1}(\mu\theta)$. Обозначая это слагаемое через $u_2\eta_0^2$, находим уравнение для $q_0(\tau_1)$, которое эквивалентно условию отсутствия резонансов в следующем виде: $$\frac{\partial q_1}{\partial \theta_1} = u_2.\tag{1.24}\label{Eqq0}$$ отсюда: $$q_1 = u_2\theta_1+q_{10}.$$ В результате окончательное решение для $\xi_2$ можно представить так: $$\xi_2 = \frac{1}{\sinh^2(\mu \theta)}\left( q_2 + 3\frac{(u_2\theta_1+q_{10})^2}{\sinh(\mu \theta)}+\int\limits_{0}^{\theta} \Big(U(\eta_0(z))-u_2\eta_0^2(z)\Big)\sinh^2(\mu z) dz \right).\tag{1.25}\label{Solxi21}$$ Здесь $q_2$ - постоянная интегрирования, зависящая от медленных переменных.
Уравнение для поля во втором порядке имеет теперь следующий вид: $$\frac{1}{\dot{\eta_0}} \left(\dot{\xi}_2 + \frac{u_2}{\sinh^2(\mu \theta)}\right) -\frac{2s u_2}{\sqrt{3}\mu}\frac{1}{\sinh(\mu \theta)}+\frac{\partial f_1}{\partial \theta_1} + \frac{\partial f_0}{\partial \theta_2} = -\dot{\eta_2}.$$ Это уравнение легко интегрируется, но как и уравнение для $\xi_2$, зависит от вида функции $U(\eta)$. Поэтому для построения решений во втором и последующих порядков необходимо уточнять общие представления о форме потенциала самодействия. В первых двух порядках вид функции не имеет значения, и вся динамика определяется начальными условиями, а также значением постоянной $v_0$, играющей роль космологической постоянной.
Объединяя полученные решения в первых двух порядках находим: $$\xi = \frac{\mu}{3} \tanh^{-1}(\mu \theta) + \varepsilon \frac{u_2\theta_1+q_{10}}{\sinh^{2}(\mu \theta)}+O(\varepsilon^2),$$ $$\eta = f_0+\frac{s}{\sqrt{6}}\ln\left(\frac{\cosh(\mu \theta)-1}{\cosh(\mu \theta)+1}\right) -\varepsilon \left(\frac{2s(u_2\theta_1+q_{10})}{\sqrt{3}\mu}\frac{1}{\sinh(\mu \theta)}-f_1(\tau_1,\ldots)\right)+O(\varepsilon^2).$$ Соответственно, решение для масштабного фактора будет иметь такой вид: $$a = \left(A_0\mu +\varepsilon \Big(A_1 - A_0(u_2\theta_1+q_{10})\tanh^{-1}(\mu \theta)\Big)\right)\sinh^{1/3}(\mu \theta)+O(\varepsilon^2).
$$ Здесь $A_0$ и $A_1$ - постоянные интегрирования.
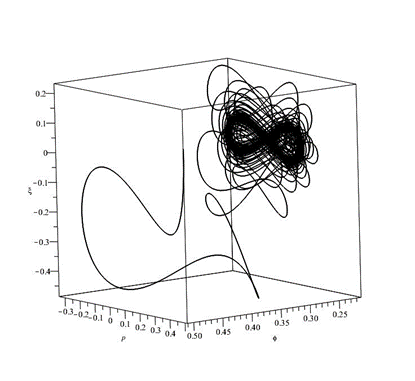
Для иллюстрации характера полученного приближения в нулевом порядке приведем сравнение численного решения задачи с потенциалом Хиггса (\ref{DefVH}) и решения, полученного с помощью ММР. Соответствующие кривые приведены на рис. 4. Можно видеть, что нулевой порядок в рассматриваемой модели для параметра Хаббла является универсальным, т.е. зависит только от значений потенциала самодействия в нуле и не зависит от его конкретной формы.
Поправки более высокого порядка требуют определенных вычислений, связанных с удовлетворением начальным условиям, что выходит за рамки данной работы.
1.7 Заключение
Приведенные в работе вычисления демонстрируют общие принципы использования метода многомасштабных разложений к задачам космологии. Как было показано, динамические системы, используемые для описания космологической динамики содержат, как правило, неявно несколько безразмерных постоянных, которые определяют тип решений. В рассмотренной
модели такими безразмерными постоянными являются масштаб поля $\Phi_0$ и параметр медленного скатывания: $p=(H_0T_0)^{-1}$. Использование ММР позволяет получить приближенные решения для физических условий, соответствующих малости этих параметров, с коррекцией скорости сходимости. При этом, полученная с помощью ММР информация о самом решении, дополняет общую информацию, которую можно получить численными методами и методами качественного анализа динамических систем. Полученные результаты указывают на возможность применения данного подхода в задачах космологии для более сложных моделей, чем рассмотренная в данной работе.
Список литетературы
1. Dolgov A.D., Zeldovich Ya.B., Sazhin M.V.Kosmologiya ranney Vselennoy(The cosmology of the earlyUniverse), Moscow: Izd. Moscow State University, 1988, 199p.4.
2. Богоявленский О.И. {\it Методы качественной теории динамических систем в астрофизике и газовой динамике}. Наука, Москва (1980)
3. Ignat’ev Yu.G. Klassicheskaya kosmologiya i temnaya ehnergiya(Classical cosmology and dark matter), Kazan:Izd. Kazan University, 2016, 248 p.5.
4. Ignat’ev Yu.G. Standard cosmological model: mathmatical, qualitatively and numerical analysis, Space, time and fundamental interaction, 2016, no. 3, pp. 17–36.
5. V.M. Zhuravlev. Qualitative analisys of cosmological models with scalar fields.
Space, time and fundamental interaction, 2016, no.4- pp. 39-51
6. V.M. Zhuravlev, S.V. Chervon. Qualitative Analysis of the Dynamics of a Two-Component Chiral Cosmological Model. Universe, 2020, Volume 6, Issue 11, 195
7. P. L. Bhatnagar. Nonlinear waves in one-dimensional dispersive systems. (Oxford, 1979)
8. Roger K Dodd, Chris J Eilbeck, John D. Gibbon, Hedley C Morris. Soliton and nonlinear wave equations. Publisher: Academic Press Inc. [Harcourt Brace Jovanovich Publishers], 1982
- Войдите на сайт для отправки комментариев
- 2962 просмотра