I. Метод функциональных подстановок
1. Линейные функциональные подстановки
Метод функциональных подстановок (МФП) в варианте, изложенном в работах [1, 2], строится на основе системы базовых соотношений относительно набора вспомогательных, вообще говоря, матричных или даже более общих типов функций. Пусть $\hat{T}$ - некоторая матричная функция переменных $x,t$ , конечной матричной размерности $N\times N$. Введем две матричных функции ${\hat A}(x,t)$ и ${\hat B}(x,t)$, которые связаны с функцией ${\hat T}(x,t)$ двумя соотношениями: $${\hat T}_x={\hat A}{\hat T},\quad {\hat T}_t={\hat B}{\hat T},\tag{1.1}\label{EqBaseT}$$ откуда следует, что эти две матричные функции удовлетворяют одному матричному соотношению: $${\hat A}_t-{\hat B}_x+[{\hat A},{\hat B}]=0,\tag{1.2}\label{EqBaseAB},$$ где $[{\hat A},{\hat B}]$ - коммутатор двух матриц. Из (1) следует множество рекуррентных дифференциальных следствий. Эти дифференциальные следствия можно записать в следующем виде: $$\frac{\partial {\hat T}}{\partial x^k\partial t^m}={\hat T}^{[k,m]}={\hat A}^{[k,m]}(x,t){\hat T},$$ где матрицы ${\hat A}^{[k,m]}(x,t)$ вычисляются из системы рекуррентных соотношений: $${\hat A}^{[k+1,m]}={\hat A}^{[k,m]}_x+{\hat A}^{[k,m]}{\hat A},$$ $${\hat A}^{[k,m+1]}={\hat A}^{[k,m]}_t+{\hat A}^{[k,m]}{\hat B},\tag{1.3}\label{EqBaseDAB}$$ $${\hat A}^{[1,0]}={\hat A},\quad {\hat A}^{[0,1]}={\hat B},\quad {\hat A}^{[1,0]}={\hat 1},~~k,m=0,1,\ldots.$$ Если в этом случае функция ${\hat T}$ удовлетворяет некоторму интегрируемому уравнению, например, линейному уравнению следующего вида: $$ \sum\limits_{k=0}^P\sum\limits_{j=0}^Q {\hat C}_{kj}\frac{\partial^{k+m}}{\partial x^k\partial t^m}{\hat T}=0,\tag{1.4}\label{EqT}$$ то с помощью рекуррентных соотношений (\ref{EqBaseDAB}) это уравнение сводится к нелинейному матричному уравнению: $$\sum\limits_{k=0}^P\sum\limits_{j=0}^Q {\hat C}_{kj}{\hat A}^{[k,j]}=0,$$ относительно матриц ${\hat A}$ и ${\hat B}$ вместе с (\ref{EqBaseAB}) составляет замкнутую нелинейную систему уравнений, решения которой могут быть найдены по решениям уравнения (\ref{EqT}) с помощью функциональных подстановок (\ref{EqBaseT}).
2. Уравнения быстрой диффузии и МФП
В качестве одного из основных объектов исследования в проекте рассматривались модели диффузионных процессов, которые описываются с помощью уравнений следующего общего вида: $$\frac{\partial n}{\partial t}=D_0\frac{\partial^2}{\partial x^2}\ln n +J(n,n_x,x,t).\tag{2.1}\label{EqFD}$$ Здесь $n$ - концентрация диффундирующей примеси или дефектов, если речь идет о диффузии в твердых телах, а $J(n,n_x,x,t)$ - некоторый внешний источник, вообще говоря, нелинейный. Такие модели имеют коэффициент диффузии следующего вида: $$D = \frac{D_0}{n(x,t)}.\tag{2.2}\label{EqD}$$ Диффузионные уравнения с таким коэффициентом диффузии часто называют уравнением быстрой диффузии (УБД) [Sem1,Sem2]. В дальнейшем мы будем придерживаться этого названия уравнений и моделей, связанных с этим уравнением.
Применение МФП к уравнениям типа (\ref{EqFD}) опирается на существование функциональной скалярной подстановки типа (\ref{EqBaseT}), сводящей уравнение: $$T_tT_x=D_0T_{xx}T\tag{2.3}\label{EqTT}$$ к уравнению УБД следующего вида: $$\frac{\partial A}{\partial t}=D_0\frac{\partial^2}{\partial x^2}\ln A+\frac{\partial}{\partial x}A.\tag{2.4}\label{EqFDs}$$ Действительно, если воспользоваться (\ref{EqBaseT}), то уравнение (\ref{EqTT}) сводится к соотношению: $$BA=A_x+A^2.$$ Разделив это соотношение на $A$ и результат продифференцировав по $x$, с учетом (\ref{EqBaseAB}) для скалярного случая приходим к уравнению (\ref{EqFDs}). Таким образом, задача построения решений уравнения (\ref{EqFDs}) сводится к задаче интегрирования уравнения (\ref{EqTT}). Заметим, что уравнение (\ref{EqFDs}) сводится к уравнению УБД без источников с помощью замены координаты по правилу: $x\to \xi=x+t$. В результате такого преобразования уравнение (\ref{EqFDs}) принимает вид: $$\frac{\partial n}{\partial t}=D_0\frac{\partial^2}{\partial x^2}\ln n,\tag{2.5}\label{EqFD0}$$ где $n(x,t)=A(x+t,t)=A(\xi,t)$. Решение этого уравнения исследовалось в [ZhTMF15], где с помощью принципа суперпозиции строились решения этого уравнения и некоторых его обобщений.
Уравнение (\ref{EqTT}) представляет лишь частный случай возможных типов нелинейных уравнений, связанных с уравнениями нелинейной диффузии скалярными подстановками (\ref{EqBaseT}). Например, уравнение: $$T_t(T_x)^k=D_0T_{xx}T^k,\tag{2.6}\label{EqTTn}$$ где $k$ - некоторое вещественное число. Используя (\ref{EqBaseT}), это уравнение приводится к уравнению нелинейной диффузии: $$\frac{\partial A}{\partial t}=\frac{D_0}{1-k}\frac{\partial^2}{\partial x^2}A^{1-k}+\frac{\partial}{\partial x}A^{2-k}.\tag{2.7}\label{EqDn}$$ Последнее уравнение представляет собой нелинейное уравнение диффузии с коэффициентом диффузии следующего вида: $$D=D_0 A^{-k}.$$
Частным вариантом этой общей схемы является уравнение: $$T_tT=D_0T_{xx}T_x,\tag{2.8}\label{EqTT2}$$ сводящееся к виду: $$\frac{\partial A}{\partial t}=\frac{D_0}{2}\frac{\partial^2}{\partial x^2} A^2+\frac{\partial}{\partial x}A^3.$$ Уравнения типа (\ref{EqTT}) и (\ref{EqTTn}) в дальнейшем будем называть уравнениями нулевой девиации (УНД).
3. Методы интегрирования УНД
Для выяснения свойств уравнений (8) и (11) , рассмотрим вспомогательное уравнение следующего общего вида: $$\Big(\Psi_t+C\Psi_x+Q\Psi\Big)\Big(\Psi_x+K\Psi\Big)=\Big(\Psi_{xx}+P\Psi_x+S\Psi_t+R\Psi\Big)\Psi\tag{3.1}\label{EqTTTT}$$ относительно вспомогательной функции $\Psi(x,t)$, в котором коэффициенты $C,Q,P,R,S,K$ также являются функциями $x,t$.
Используя подстановки (1.1) уравнение (\ref{EqTTTT}) можно превратить в уравнение: $$(B+CA+Q)(A+K)=A_x+A^2+PA+SB+R,$$ связывающее две вспомогательных функции $A$ и $B$ между собой. Делая формальную замену: $A=n-K+S$ и исключая из последнего соотношения функцию $A$ с использованием (1.3), приходим к обобщенному варианту уравнения (1.1): $$\frac{\partial n}{\partial t}=D_0\frac{\partial^2 \ln{n}}{\partial x^2}+\frac{\partial}{\partial x}\left((1-C)n+\frac{L}{n}\right)+F_x+K_t,\tag{3.2}\label{EqDln}$$ Здесь: $$F=Q-C(H-S-2)-P,$$ $$L=R-QS-H_x+H^2-PH+CHS,$$ $$H=K-S.$$ Если найдено решение (1..2) относительно функции $\Psi(x,t)$, то решение уравнения (12) находится с помощью функциональной подстановки: $$n=T_x/T+H.$$ Таким образом, задача отыскания решений уравнения (1.13) сводится к построению решений (1.12). Решение уравнения (1.12) могут быть найдены различными способами. Одним из таких способов является приведение уравнения (12) к паре уравнений следующего вида: $$\Psi_t+C\Psi_t+(Q-M)\Psi=0,$$ $$\Psi_{xx}+(P-M)\Psi_x+S\Psi_t+(R-KM)\Psi=0,$$ где $M(x,t)$ - функция разделения уравнений. Система (1.15) представляет собой систему из двух линейных уравнений, подобную системе представления Лакса в теории солитонов. Вычисляя условия совместности этих уравнений, можно получить решения уравнения (1.13). Введем обозначения: $${\hat {\bf L}}=\frac{\partial}{\partial t}+C\frac{\partial}{\partial x}+U$$ $${\hat {\bf M}}=\frac{\partial^2}{\partial x^2}+V\frac{\partial}{\partial x}+W.$$ Здесь: $$U=Q-M,\quad V=P-M-SC, \quad W=R-KM-SR+SKM.$$ Условие совместности можно представить в виде условия коммутавтивности операторов ${\hat {\bf L}}$ и ${\hat {\bf M}}$ по модулю оператора ${\hat {\bf M}}$: $$[{\hat {\bf L}},{\hat {\bf M}}]={\hat {\bf D}}{\hat {\bf M}}$$
Это условие эквивалентно двум уравнениям на три коэффицента $U,V,W$ : $$V_t-C_{xx}+VC_x+CV_x-2U_x=0,$$ $$W_t-VU_x+CW_x-U_{x}.\tag{3.3}\label{EqWUV}$$ Первое уравнение представляет собой дифференицальный закон сохранения, который эквивалентен следующей системе уравнений: $$V=\Theta_x,\quad C_x-VC+2U=\Theta_t.\tag{3.4}\label{EqUV}$$ Решение системы уравнений (\ref{EqWUV}) - (\ref{EqUV}) может быть получено с помощью метода преобразований Дарбу [ZHM] для системы уравнений (15) при условии, указания спектрального параметра, входящего в запись коэффицентов $U,V,W$ операторов ${\hat {\bf L}}$ и ${\hat {\bf M}}$. Таким образом, основной задачей построения решений уравнения (13) является введение нетривиального спектрального параметра в коэффиценты $U,V,W$ таким образом, чтобы коэффиценты $C,L,F,H$ уравнения (\ref{EqDln}) не зависили от этого спектрального параметра. Эта задача будет решаться на слендующем этапе проекта. Однако рамках проекта рассматриваются и другие способы построения решений уравнения (12).
4.1. Решение с внешним источником
В качестве альтернативных методов построения решений уравнений УНД приведем специальный способ вычисления решений уравнения (\ref{EqTT}) и его обобщения следующего вида: $$(T_t-(gx+ct) T)T_x=T_{xx}T,~~g,c={\rm const}.\tag{4.1}\label{EqTTg}$$ Последнее уравнение с помощью скалярных подстановок (\ref{EqBaseT}) приводится к следующему виду: $$ \frac{\partial A}{\partial t}=D_0\frac{\partial^2}{\partial x^2}\ln A+\frac{\partial}{\partial x}A + g,\tag{4.2}\label{EqAg}$$ что соответствует УБД с постоянным по пространству источником $g={\rm const}$. Представим уравнение (\ref{EqTTg}) в следующей форме:$$(\Phi_t+gx+ct)\Phi_x=\Phi_{xx}+(\Phi_x)^2,\tag{4.3}\label{EqPhi}$$ где $\Phi = \ln T$. Будем искать решение для $\Phi$ в следующем виде$$\Phi=\Phi_1(x,t)+\Phi_2(x,t)$$ и потребуем, чтобы функции $\Phi_1$ и $\Phi_2$ удовлетворяли дополнительной паре уравнений:$$\Phi_{1,t}=v_{1}\Phi_{1,x},\quad \Phi_{2,t}=v_{2}\Phi_{2,x}.\tag{4.4}\label{SbusPhi}$$ Подставляя эти соотношения в (\ref{EqTTg}), приходим к уравнению:$$\Phi_{1,xx}+\Phi_{2,xx}+(1-v_{1})\Big(\Phi_{1,x}\Big)^2+(1-v_{2})\Big(\Phi_{2,x}\Big)^2- \tag{4.5}\label{EqPhi12}$$ $$ -(gx+ct)\Phi_{1,x}-(gx+ct)\Phi_{2,x} +(2-v_{1}-v_{2})\Phi_{1,x}\Phi_{2,x}=0.$$ Условием разделения этого уравнения на уравнения только для каждой из функций по отдельности является условие:$$v_1+v_2=2.\tag{4.6}\label{Eqaa}$$ В этом случае функции $\Phi_1$ и $\Phi_2$ удовлетворяют по отдельности двум дополнительным уравнениям: $$\Phi_{1,xx}+(1-v_{1})\Big(\Phi_{1,x}\Big)^2 -(gx+ct)\Phi_{1,x}=p(x,t),\tag{4.7}\label{EqPhi12x}$$ $$\Phi_{2,xx}-(1-v_{1})\Big(\Phi_{2,x}\Big)^2 -(gx+ct)\Phi_{2,x}=-p(x,t).$$ Рассмотрим случай $v_1={\rm const}$. Тогда из (\ref{SbusPhi}) следует: $$ \Phi_1=\Phi_1(x+v_1t),~~\Phi_2=\Phi_2(x+v_2t),~~v_2=2-v_1.$$ Поскольку функции $\Phi_1$ и $\Phi_2$ зависят каждая от своей бегущей переменной $\xi=x+v_1 t$ и $\eta=x+v_2 t$, соответственно, то коэффициенты уравнений также должны зависеть только от этих переменных. Однако в оба уравнения входит один и тот же коэффициент $gx+ct$, который должен выражаться либо через $\xi$, либо $\eta$. Предположим для определенности, что $gx+ct=g(x+v_1 t)=g\xi$. Это эквивалентно условию: $c=gv_1$. Тогда первое уравнение системы (\ref{EqPhi12x}) будет иметь такой вид: $$\Phi''_{1}+(1-v_{1})\Big(\Phi'_{1}\Big)^2 -g\xi\Phi'_{1}=p(x,t),$$ откуда следует, что функция $p(x,t)$ также должна быть функцией $\xi$. Второе уравнение теперь содержит переменную $\xi$. Это означает, что функция $\Phi_2$ может быть только линейной функцией $\eta=x+v_2 t$. Таким образом, $\Phi=\lambda\eta+\Phi_0$. Подставляя это решение для $\Phi_2$ во второе уравнение (\ref{EqPhi12x}), находим: $$-(1-v_1)\lambda^2-g\xi\lambda=-p(x,t).$$ Таким образом, уравнение для $\Phi_1$ будет иметь следующий окончательный вид: $$\Phi''_{1}+(1-v_{1})\Big(\Phi'_{1}\Big)^2 -g\xi\lambda \Phi'_{1}=g\lambda\xi+(1-v_1)\lambda^2\tag{4.8}\label{EqPhi1m}$$ Уравнения (\ref{EqPhi1m}) преобразуются к линейному уравнению с помощью следующей подстановки:$$\Phi'_{1}=\frac{1}{1-v_{1}}\frac{\partial \ln \Psi_{1}}{\partial \xi}.$$ Уравнение для $\Psi{1}$ будут теперь иметь следующий вид: $$\Psi''_{1}-g\xi \Psi'_{1}=(1-v_{1})\Big(g\lambda\xi +(1-v_1)\lambda^2\Big)\Psi_{1}.\tag{4.9}\label{EqPsi1}$$ Это уравнение c помощью замены $\Psi_1= e^{g\xi^2/4}F(\xi)$, приводится к уравнению: $$F''-\Big(g\xi^2/4+k\xi+m\Big)F=0,\tag{4.10}\label{EqF}$$ где введены обозначения: $$k=(1-v_{1})g\lambda,~~m=(1-v_1)^2\lambda^2-g/2.$$ Уравнение (\ref{EqF}) представляет собой уравнение Шредингера для квантового гармонического осциллятора. Если обозначить через $F_1(\xi)$ и $F_2(\xi)$ два линейно-независимые решения (\ref{EqF}), тогда решение для $\Phi$ можно представить в следующем виде: $$\Phi = \Phi_1+\Phi_2=\lambda \eta +\Phi_0 + {\frac{1}{1-v_{1}}}\Big(g\xi^2/4+\ln\Big(c_1F_1(\xi)+c_2F_2(\xi)\Big)\Big)$$ где $c_1$ и $c_2$ - произвольные постоянные. Решение уравнения (\ref{EqAg}) теперь можно записать так: $$A = \frac{\partial \Phi}{\partial x}= \lambda + {\frac{1}{1-v_{1}}}\left(\frac{g\xi}{2}+\frac{\partial}{\partial x}\ln\Big(c_1F_1(\xi)+c_2F_2(\xi)\Big)\right).\tag{4.11}\label{SolAg}$$ Полученное решение представлет собой бегущую волну с фазовой скоростью $v_1$. В случае выбора граничного услоаия для функции $F$ вида $F\to 0$ при $x\to\pm\infty$, что соотвествует известным решениям вида: $F=H_n(\xi)e^{-xi^2/2}$, где $H_n(\xi)$ - полиномы Эрмита, решение для $A$ будет сингулярным. Сингулярности будут располагаться в нулях полиномов Эрмита, число которых зависит от порядка $n$ этих полиномов. Однако условие $F\to 0$ при $\xi\to\pm\infty$ для рассматриваемый решений не отражает каких-либо существенных особенностей процесса диффузии в рассматриваемом случае. Более приемлемым является условие $A\to A_{\pm}$ $\xi\to\pm\infty$, где $A_{\pm}$ - некоторые постоянные. Однако такие условия строятся уже численно.
4.2. Решение без источника
В случае если $g=c=0$ для каждой из функций $\Phi_{\alpha},~\alpha=1,2$ существует замена: $$\Phi'_{1}=\frac{1}{1-v_{1}}\frac{\partial \ln \Psi_{1}}{\partial \xi},$$ $$\Phi'_{2}=\frac{1}{1-v_{2}}\frac{\partial \ln \Psi_{2}}{\partial \eta},$$ которая сводит уравнения (\ref{EqPhi12x}) к линейным уравнениям относительно функций $\Psi_1$ и $\Psi_2$: $$\Psi''_{1}=(1-v_{1})p\Psi_{1},~~\Psi''_{2}=(1-v_{1})p\Psi_{2}.\tag{4.12}\label{EqPsi12}$$ При этом $p={\rm const}$. В результате, решение для $\Phi$ будет иметь такой вид: $$\Phi=\frac{1}{1-v_{1}}\left(\ln\Psi_1(\xi)-\ln\Psi_2(\eta)\right).$$ Решение уравнений имеют вид: $$\Psi_1(\xi)=a_1 e^{\mu\xi}+a_2 e^{-\mu\xi},\quad \Psi_2(\eta)=b_1 e^{\mu\eta}+b_2 e^{-\mu\eta},$$ где $a_1,a_2,b_1,b_2$ - произвольные постоянные и $\mu=\sqrt{(1-v_1)p}$. Соответственно: $$A=\Phi_x=\frac{1}{1-v_{1}}\frac{\partial}{\partial x}\ln\left[\frac{a_1 e^{\mu\xi}+a_2 e^{-\mu\xi}}{b_1 e^{\mu\eta}+b_2 e^{-\mu\eta}}\right].\tag{4.12}\label{SolAg0}$$ Пример данного типа решения приведен на рис. 1.
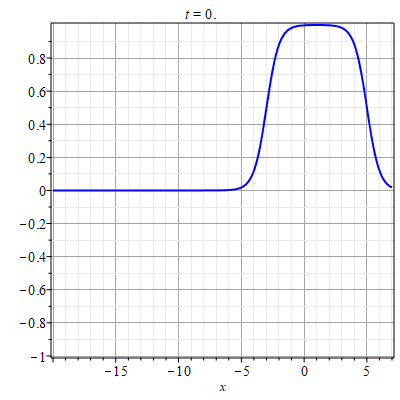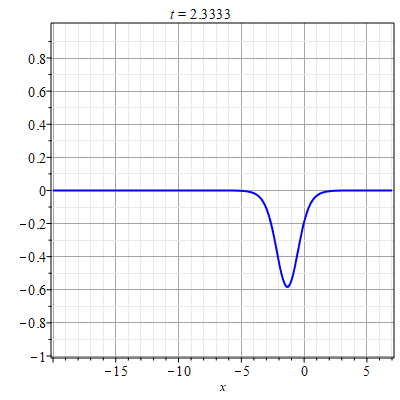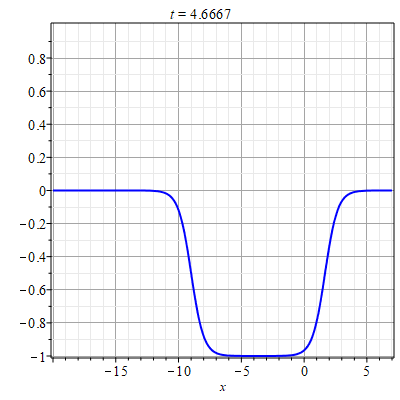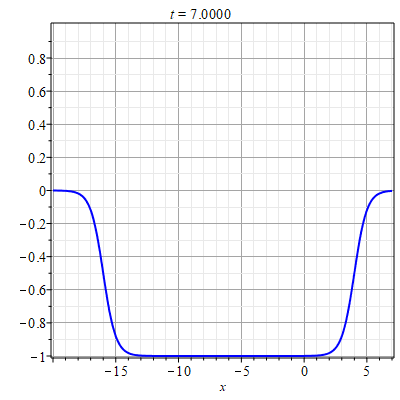 |
| Рис. 1. Пример решения (\ref{SolAg0}) для парамтров: $v=3$, $\mu=1$, $a_1=b_1=1$, $a_2=e^{-10}$, $b_2=e^{6}$. |
Рис. 1 демонстрирует развитие автоволны в форме сужения области с еденичной концентрацией.
- Войдите на сайт для отправки комментариев
- 4504 просмотра